Determinism
Written by Areeba Abid Fall 2015
Edited by Richard Udall Summer 2019
Determinism is a metaphysical principle which states that if one has full knowledge of a systems initial conditions and the physical laws which governs the system, then it is possible to predict the evolution of the system arbitrarily far into the future. There are two significant complications to this principle. The first is the defining feature of what is known as chaos: it is impossible to know the initial conditions of the system perfectly, and in a sufficiently complex system extremely small differences in initial conditions will lead to very substantial differences at later points of time. This type of chaos is still deterministic, as the laws governing the system mean that a single input corresponds to a single output. This contrasts with systems which may have some inherent degree of randomness, which notably includes the current paradigm of all quantum mechanical system.
Main Idea
Concepts of Physical and Philosophical Determinism
Newton's laws allow us to predict the motion of an object if we know the initial position, initial momentum, and forces acting on the object. If this idea is extrapolated to all objects in the universe, it would seem that we could predict the future of the entire universe if we only knew the initial conditions (the starting positions, momenta, and interaction forces) of each object. In philosophy and metaphysics, this principle has been used to argue that humans do not have free will, because the atoms that make up our bodies simply continue to move in the paths we would expect based on their initial conditions.
Deterministic Chaos
Based on an understanding of Newton's Laws, is may seem certain that determinism is correct. However, the story is more complicated, and in one manner or another those complications are the basis of most modern physics.
The first practical limitation is the fact that the initial conditions of a system may only be measured as accurately as our instruments allow. In most systems, uncertainties grow over time, which means the even small errors at the beginning may lead to drastic differences between predictions and reality after a given time period. This is why iterative prediction is generally only reliable for small time scales, although the exact nature of the system may cause the relevant time scales to vary drastically. In an idealized projectile motion problem, errors in the initial condition will generally have a linear effect upon the error of the prediction, which is manageable. If one introduces more complex forces, such as air resistance, these errors may be amplified much more substantially.
A related limitation is our use of phenomenology. We treat a billiard ball, for example, as a single object, when in fact it is a collection of atoms. Modelling the ball correctly would require modelling each of these atoms and their interactions, but this is well beyond our capabilities, and so we use approximate forces instead of considering the truly fundamental forces. Even if we did have a unified theory of everything, it would be functionally impossible for us to apply it to the universe, and so the dream of fully predicting a system is beyond our reach as humans.
The limitations described above give rise to what is known as deterministic chaos[1]. This is a major field of study in modern physics, and is quite complicated and challenging. One may note, for example, that there is a million dollar prize for anyone who can prove that solutions exist for the Navier-Stokes equations, which govern the behavior of fluids[2]. As such, this section will focus n use computational modeling to observe the behavior of chaos, rather than trying to explain it. That being said, chaos theory is a specialty of the Georgia Tech physics department, and if you are interested in learning more there are a wealth of resources to explore.
Stochastic Systems
A stochastic system is one with an inherent amount of randomness. This may be introduced by the limitations above, but it may also have more fundamental roots. When one moves past Newton's theory, the idea of determinism is called into question. Relativity behaves nicely from this respect, being (to the best of our knowledge) a purely deterministic theory. Quantum mechanics, however, seems by its very nature to defy determinism: quantum states always have a degree of randomness, and so it is impossible to fully determine the future of a quantum system. None of this is certain, of course, since we still lack a unified field theory, and there is an argument to be made, such as is made by Gerard t'Hooft[3], that this theory will be deterministic, but we have no way to know at this time.
Mathematical Model
There is little that can be said in formal mathematical terms about chaotic systems without making use of advanced mathematical techniques. We will note a few properties of chaotic equations though. Firstly, all chaotic systems are non-linear (but not all non-linear systems are chaotic), which is when changes to the input value (i.e. initial conditions) do not correspond to linear changes in the output value, as we've already described. Our equation for quadratic air resistance is non-linear, but is not chaotic, so what's the difference? The second attribute of chaos is informally called mixing. This means that if you start many points next to each other and trace out their trajectories, those trajectories will end up looking like a hopelessly tangled bowl of spaghetti, and will fill up the whole space. The formal way of quantifying this is complicated, so we'll leave it there, but ChaosBook can give more detail.
Computational Modeling
Computational modelling consists of putting any non-linear system into a relevant numerical simulator, such as the one used in Predicting Change in multiple dimensions. Care must be paid that time steps are suitably small, and initial conditions carefully noted, since by nature chaotic systems are very sensitive to minute alterations in these parameters.
Examples
All of these examples should be performed with the use of a numerical solution program, such as this. You should note that it is unlikely for you to have these sorts of problems in this class, but they are included to provide a flavor of the field beyond purely conceptual ideas.
Simple
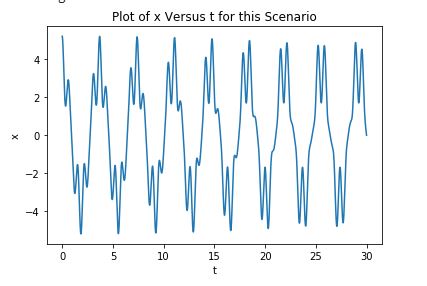
Using the chaotic spring system from Predicting Change in multiple dimensions, set [math]\displaystyle{ k = 100 }[/math], [math]\displaystyle{ \theta_0 = \pi/3 }[/math], equilibrium length [math]\displaystyle{ L_{eq} = 4 \; m }[/math], and initial extension [math]\displaystyle{ L_{init} = 6 \; m }[/math], then run for a duration of 30 seconds with a time step of 0.00001 seconds. Describe how this behavior differs from that of a normal pendulum, and note the final x position and number of of quasi-periods. Set [math]\displaystyle{ L_{eq} = 4.1 \; m }[/math], and note the difference in final x position and the number of quasi-periods. Do the same set of calculations with the corresponding pendulum system (i.e. have one round set to [math]\displaystyle{ L = 4 \; m }[/math] and another with [math]\displaystyle{ L = 4.1 \; m }[/math] , and note the change in final x position and number of oscillations between the two for this system. Compare the two systems.
First, one may look at the graph to see that the behavior is fairly different from that of a pendulum, but that the same fundamental swinging motion remains (as one might expect).
Looking at specific values, one has that the final x position in the first case for the spring is approximately [math]\displaystyle{ x_f = 0 \; m }[/math], whereas in the second case it is approximately [math]\displaystyle{ x_f = 2.5 \; m }[/math]. The number of oscillations goes from around 8.25 to around 7.8. The pendulum system has [math]\displaystyle{ x_f \approx 3.25 \; m }[/math] in the first case and [math]\displaystyle{ x_v \approx 3 \; m }[/math] in the second case, with the number of oscillations only decreasing slightly from around 8 to around 7.9. Thus, one can see that a minor change in the initial conditions has more effect upon the spring than upon the pendulum. You can also see in the general behavior of the spring how there exist many turning points, and some nested behavior, with small pseudo-oscillations of higher frequencies on top of the larger oscillations. Because the system is chaotic, these are not truly periodic (if they were we could decompose it into a series of higher frequency and lower amplitude components), but they do approximately resemble such behavior on these time scales (more interesting things happen the longer one goes).
Middling
Now, put the following system into a numerical solution program, setting mass equal to [math]\displaystyle{ 1 \; kg }[/math], and choosing whichever initial conditions you would like (though try to keep the numbers all between -1 and 1):
[math]\displaystyle{ F_x = (\frac{1}{10})(x^2-y^2-x) }[/math]
[math]\displaystyle{ F_y = (\frac{1}{10})(2xy + y) }[/math]
View the paths in the x-y plane, and think about why the trajectories follow the way they do (in particular, note the shapes as they relate to shapes one may recognize. This set of equations is a form of the Hénon Horseshoe, and comes from [4]. The trajectories appear to overlap in places. Does this make sense? Explain why this happens.
This problem has a fairly simple answer, which is instructive in mechanics as a whole. The trajectories here appear to overlap because they have different velocities even at the same value of [math]\displaystyle{ (x,y) }[/math]. This is only possible because the equations are defined in terms of acceleration rather than velocity. If we could look at this in 4 dimensions, two of velocity and two of position, we would see the "spaghetti" does not overlap. Any deterministic dynamical system must not have overlap in these 4 dimensions, because otherwise one would have different motions from the same set of inputs, which would violate determinism.
Difficult
Let's now consider the Lorenz system, which is one of the most iconic chaotic systems appearing, among other places, at the top left of this page. It is a system which "predicts" the "weather", but it is more interesting because of its easily identifiable chaotic properties and relatively easy to solve parameters. The Lorenz system is defined by the equations
[math]\displaystyle{ v_x = \sigma(y-x) }[/math]
[math]\displaystyle{ v_y = x(\rho - z) }[/math]
[math]\displaystyle{ v_z = xy - \beta z }[/math]
Where for our purposes [math]\displaystyle{ \sigma = 10 }[/math], [math]\displaystyle{ \rho = 28 }[/math], and [math]\displaystyle{ \beta = 8/3 }[/math]. We would like to solve this with our Newton's laws solver, but we have a problem: these equations are in terms of velocities, not accelerations. However, with a little calculus, we can express them as
[math]\displaystyle{ a_x = \sigma(v_y - v_x) }[/math]
[math]\displaystyle{ a_y = -v_x z-x v_z+rv_x -v_y }[/math]
[math]\displaystyle{ a_z = v_x y + v_y x - bv_z }[/math]
If you have had calculus the method of getting here should be fairly obvious, if not don't worry about it. We'll be assuming mass [math]\displaystyle{ m = 1 \; kg }[/math], and so will treat force and acceleration as equivalent. Now, depending on your experience with calculus, you may notice something important here: in order for our second set of equations to be the same as our first, we need to set two sets of initial conditions: both position and velocity, and the latter must be set so that they conform to the first set of equations. If we don't fix these, we'll instead have a system equivalent to the Lorenz system plus some other constants, which is not what we want. Thus, the first part of the question: choose some initial position (make sure NOT to choose [math]\displaystyle{ \vec{r} = (0,0,0) }[/math] for this, for reasons we will see in a little while), and calculate the correct initial velocity to go along with it. Then, plug this along with the equations of motion into the simulator (I have already done so for my set of initial conditions: [math]\displaystyle{ \vec{r} = (0.1,-0.3,-0.2) }[/math]). Let it run, and you should get a butterfly image (this will require having 2 coordinate slices, such as an x-y graph, etc.). You should notice that it is circling around two points: these are called the system's stationary points, because if we started at one of them then the system wouldn't go anywhere. You can calculate these yourself with only algebra, and should now do so (hint: if it's stationary, that means its velocity must be equal to zero). There should be 3 stationary points from this solution, one of which should be familiar from earlier in this problem. Finally, try starting the simulation at one of these points (make sure to recalculate the velocities correctly), and check that it is indeed stationary.
To begin, here is the arithmetic to get the initial velocity given my chosen initial position of [math]\displaystyle{ \vec{r} = (0.1,-0.3,-0.2) }[/math]:
[math]\displaystyle{ v_{x0} = 10((-0.3)-(0.1)) = -4 }[/math]
[math]\displaystyle{ v_{y0} = (0.1)(28 - (-0.2))-(-0.3) = 3.12 }[/math]
[math]\displaystyle{ v_{z0} = (0.1)(-0.3) - (\frac{8}{3})(-0.2) = 0.50\bar{3} }[/math]
Now, let's compute the stationary points. First, setting [math]\displaystyle{ v_x = 0 }[/math] directly gives that
[math]\displaystyle{ x_{eq} = y_{eq} }[/math]
Next, plugging that into [math]\displaystyle{ v_y = 0 }[/math] gives us that
[math]\displaystyle{ 0 = y_{eq} (\rho - z_{eq} - 1) \Rightarrow z_{eq} = \rho - 1 }[/math] or [math]\displaystyle{ y_{eq} = 0 }[/math]
Finally, we can use [math]\displaystyle{ v_z = 0 }[/math] to look at both cases. We can see that
[math]\displaystyle{ 0 = x_{eq}y_{eq} - \beta z_{eq} = y_{eq}^2 - \beta z_{eq} \Rightarrow y_{eq} = \pm \sqrt{\beta z_{eq}} }[/math]
If [math]\displaystyle{ y_{eq} = 0 }[/math], this means that [math]\displaystyle{ z_{eq} = 0 }[/math], and since [math]\displaystyle{ y_{eq} = x_{eq} }[/math], we also get [math]\displaystyle{ x_{eq} = 0 }[/math]. This then is the reason why we wanted to avoid the initial position [math]\displaystyle{ \vec{r} = (0,0,0) }[/math]: if we had started there, we wouldn't have gotten any behavior at all. Now, let's look at the other case, where [math]\displaystyle{ z_{eq} = \rho - 1 }[/math]. Then we have
[math]\displaystyle{ y_{eq} = x_{eq} = \pm \sqrt{\beta(\rho - 1)} }[/math]
These two solutions should be the points you see the system orbiting, although since the orbits aren't perfect circles it is difficult to pinpoint the center. Starting the system here with the appropriate initial conditions will yield a system that does indeed stand still, although our second order way of writing this means this will always happen (to be precise, if the velocity is equal to zero, you can see above that the accelerations will always equal zero, so setting the initial velocities equal to zero for any initial position will correspond to adding just the right constants to the velocity equations to make that initial point one of the stationary points).
Connectedness
Connection to Personal Interest: Philosophical Determinism
How is this topic connected to something that you are interested in?
Determinism has fascinating implications for the concept of free will. Even if it is impossible for us to calculate the future behavior of a system accurately, it is still without a doubt the direct result of the initial conditions, as directed by Newton's laws. Consider the human body as a physical system. If the body is simply a collection of particles and thoughts in the brain are just neurons firing, is every feeling experienced and every decision made by a person simply the result of whatever initial conditions they started with? Is it possible to differentiate between the laws that regulate matter and the laws that regulate our own bodies? What happens when we try to apply the laws of physics to the workings of our minds? It's difficult to think of your body as a collection of chemicals that behave like a very complicated deterministic system, but the implications are mind blowing and have been the subject of controversy since ancient times.
Connection to Major: Engineering Applications
How is it connected to your major (biomedical engineering)?
Predicting the behavior of physical systems is important for any engineer, and determinism makes this possible to some extent.
Connection to Industry: Ethernet Data Transfer
Is there an interesting industrial application?
Data transmission takes time, and knowing the time that it takes for information to travel from one location to another is important is some industrial applications, such as sending control variables to a high-speed CNC mill. Engineers need to be able to know how long it will take for a machine to receive data, and if a system is deterministic this can be calculated. However, Ethernet systems are not deterministic and the rate of data transfer is unpredictable, which poses problems for engineers.[5]
History
The concept of determinism has been around for centuries and was explored by thinkers around the world. Physical determinism was bolstered by Newton's Laws, and the first publication discussing it in a scientific context, "LaPlace's demon", was written by Pierre Laplace in 1814[6]. He wrote that a hypothetical omniscient observer could potentially predict the entire future of the universe. Even though this is practically impossible for any human or computer to ever achieve, LaPlace argued that it was still hypothetically possible if physical determinism were true. However, in the early 20th century the development of quantum mechanics made this position substantially more complicated. In particular, the deterministic form proposed by Einstein, known as a hidden variable theory (which held that there was a correct value which the universe would act upon deterministically, but which was "hidden" from us) was put to the test in the second half of the 20th century by the Bell Inequalities [7]. Quantum mechanics has since been proven to violate the Bell Inequalities, meaning it is not a hidden variable theory (at least, of the type Einstein proposed), and the modern understanding requires that for quantum mechanics to be deterministic, it would have to sacrifice some other desirable quality like locality (the requirement that objects are only immediately affected by their immediate surroundings, so any action at a distance has to move at the speed of light) [8], or something even more exotic like unitarity (the requirement that all probabilities add to 1).
Concurrently with the development of quantum mechanics, the 20th century saw great progress in the field of deterministic chaos. Notable developments include Lorenz's discover of the Lorenz attractor in the early 60's [9], Steven Smale's many contributions [10] (made in between participating in Berkley's first famous protests), and the work of many, many others [11]
See also
- Newton's Second Law: the Momentum Principle
- Iterative Prediction
- Kinematics
- Fundamentals of Iterative Prediction with Varying Force
- Predicting Change in multiple dimensions
- Terminal Speed
- Two Dimensional Harmonic Motion
- System & Surroundings
- Entropy
External Links
Background Physics
General Information on Determinism
More on Free Will
- Khan Academy/MIT: The Problem of Free Will
- Video Arguing Free Will Doesn't Exist
- Video Arguing Free Will Does Exist (Sort Of)
Further Reading
- Matter and Interactions, 4th Edition
References
- ↑ http://chaosbook.org/ Chapter 1
- ↑ https://en.wikipedia.org/wiki/Navier%E2%80%93Stokes_existence_and_smoothness
- ↑ https://arxiv.org/pdf/quant-ph/0212095.pdf
- ↑ http://sprott.physics.wisc.edu/pubs/paper333.pdf
- ↑ http://www.automationworld.com/networking-amp-connectivity/understanding-ethernet-speed-and-determinism Understanding Ethernet Speed and Determinism
- ↑ http://www.stsci.edu/~lbradley/seminar/laplace.html
- ↑ Townsend, J.S. A Modern Approach to Quantum Mechanics, (University Science Books, Mill Valley C.A., 2012), 2nd Edition, pg. 156)
- ↑ Townsend pg. 160
- ↑ https://www.britannica.com/biography/Edward-Lorenz
- ↑ https://www.britannica.com/biography/Stephen-Smale
- ↑ ChaosBook, Appendix A