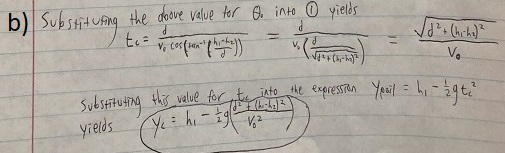Kinematics

Edited by YorickAndeweg June 2019

Edited by Richard Udall July 2019

Kinematics is the branch of mechanics which describes the motions of particles, using knowledge only of position, time, and their related quantities velocity and acceleration (formally, these are the derivatives of position with respect to time). As such, kinematics is used once one already knows all the forces acting on the particle, at which point one uses Newton's second law to determine acceleration and proceed from there. The kinematics discussed here will specifically be constant acceleration kinematics, meaning that [math]\displaystyle{ \vec{a} }[/math] will be a vector with fixed magnitude and direction for the duration of the given problem. This therefore constitutes a small and heavily idealized set of conditions, but they are instructive nonetheless.

The Main Idea

Kinematics is concerted the relationships between time and the position, velocity, and acceleration of particles, without regard for the forces that cause the acceleration. The equations that describe these relationships are called the kinematic equations, which are one of the fundamental tools of physics. Taken in combination with other fields of physics, these kinematic equations allow one to predict the motion of an object at different points in time. For example, one may use equations outside the scope of kinematics to calculate the magnitude and direction of a force acting on a particle, as well as the acceleration that the particle undergoes as a result. Then, kinematic equations might be used to calculate the position and speed of the particle as functions of time based on the acceleration found.

Quantities of Kinematics

Kinematics is concerned primarily with four variables, and may on occasion extend to include others. These variable are:

Time ([math]\displaystyle{ t }[/math])
Position ([math]\displaystyle{ \vec{r} }[/math])
Velocity ([math]\displaystyle{ \vec{v} }[/math])
Acceleration ([math]\displaystyle{ \vec{a} }[/math])
Subsequent Time Derivatives of Position (less common)

Many of the values listed above depend on the Frame of Reference, or coordinate system, chosen because the reference frame defines which points in space and time are considered x = 0, y = 0, z = 0, and t = 0. The following kinematic equations assume a reference frame of arbitrary spatial origin but with time [math]\displaystyle{ t=0 }[/math] defined as the time at which the particle is in its initial position. This assumption is made to avoid having to write [math]\displaystyle{ \Delta t }[/math] instead of [math]\displaystyle{ t }[/math] everywhere the time variable occurs, and because other definitions of [math]\displaystyle{ t=0 }[/math] are rarely used.

Subscripts of i and f respectively denote the initial and final values of these quantities over some time interval, the beginning of which is [math]\displaystyle{ t=0 }[/math].

A Mathematical Model

The Kinematic Equations

These are the standard kinematic equations that are often used to model motion in physics^[1]. That said, other equations do exist (for example, calculus-based versions of the above equations that do not assume constant acceleration, as well equations that refer to the higher time derivatives of position such as jerk).

[math]\displaystyle{ \vec{r}_f = \vec{r}_i + \vec{v}_{avg} \cdot t }[/math]
[math]\displaystyle{ \vec{v}_f = \vec{v}_i + \vec{a}_{avg} \cdot t }[/math] (Typically this equation is used in situations of constant acceleration, where [math]\displaystyle{ \vec{a}_{avg} }[/math] is that constant acceleration.)
[math]\displaystyle{ \vec{v}_{avg} = \frac{\vec{v}_i + \vec{v}_f}{2} }[/math] (Assumes constant acceleration. A derivation for this formula is available here.)
[math]\displaystyle{ \vec{r}_f = \frac{1}{2} \vec{a} \cdot t^2 + \vec{v}_i \cdot t + \vec{r}_i }[/math] (Assumes constant acceleration.)
[math]\displaystyle{ v_f^2 = v_i^2 + 2 \vec{a}(\vec{r}_f - \vec{r}_i) }[/math] (Assumes constant acceleration.)

Usually when kinematic equations are used to solve problems, one-dimensional versions are used so that vector addition doesn't need to be performed. For example, equation 4 can be decomposed into x and y components as follows:

[math]\displaystyle{ x_f = \frac{1}{2} a_x \cdot t^2 + v_{x, i} \cdot t + x_i }[/math]

[math]\displaystyle{ y_f = \frac{1}{2} a_y \cdot t^2 + v_{y, i} \cdot t + y_i }[/math]

Derivation

These equations are best derived with calculus, but it is possible to derive them without its use. First, we begin with the definition

[math]\displaystyle{ v_{avg} = \frac{\vec{r}_f - \vec{r}_i}{t} }[/math]

from which (1) follows immediately. Now, let us assume constant force, which implies constant acceleration (in the case of constant mass, which we will assume in most cases for this course) through the expression of Newton's Second Law: the Momentum Principle

[math]\displaystyle{ \vec{F} = m\vec{a} }[/math]

Since we also have acceleration by definition as

[math]\displaystyle{ \vec{a} = \frac{\vec{v}_f - \vec{v}_i}{t} }[/math]

Then similar to (1), (2) follows from rearrangement. Furthermore, (3) is the definition of an average under the assumption of linear change (which follows from constant acceleration). Now we come to the interesting equations. Expanding (1) using (3) gives

[math]\displaystyle{ \vec{r}_f = \vec{r}_i + \frac{\vec{v}_f +\vec{v}_i}{2}t }[/math]

Now, we do a rearrangement trick:

[math]\displaystyle{ \vec{r}_f = \vec{r}_i + \frac{\vec{v}_f-\vec{v}_i}{2}t + \vec{v}_i \cdot t = \vec{r}_i + \vec{v}_i \cdot t + \frac{\vec{a}}{2}t^2 }[/math]

Which is (4). Next, we rearrange this a little and multiply both sides by [math]\displaystyle{ 2 \vec{a} }[/math] to get

[math]\displaystyle{ \vec{r}_f - \vec{r}_i = \vec{v}_i \cdot t + \frac{\vec{a}}{2}t^2 }[/math]

[math]\displaystyle{ 2(\vec{r}_f - \vec{r}_i)\cdot \vec{a} = 2\cdot\vec{a}\cdot\vec{v}_i\cdot t + \vec{a}^2\cdot t^2 }[/math]

Substituting in the definition of [math]\displaystyle{ \vec{a} }[/math] for only the right side gives

[math]\displaystyle{ 2(\vec{r}_f - \vec{r}_i)\cdot \vec{a} = 2\cdot\frac{\vec{v}_f-\vec{v}_i}{t}\cdot\vec{v}_i\cdot t + (\frac{{v}_f-\vec{v}_i}{t})^2\cdot t^2 }[/math]

[math]\displaystyle{ 2(\vec{r}_f - \vec{r}_i)\cdot \vec{a} = 2\vec{v}_f\cdot\vec{v}_i -2\vec{v}_i^2 + \vec{v}_f^2 - 2\vec{v}_f\cdot\vec{v}_i + \vec{v}_i^2 }[/math]

[math]\displaystyle{ 2(\vec{r}_f - \vec{r}_i)\cdot \vec{a} + \vec{v}_i^2 = \vec{v}_f^2 }[/math]

Thus we have arrived at equation (5). One may justly ask why we chose to jump through these hoops, and the answer is, for (4) and (5) respectively, calculus and the Work/Energy theorem. That being said, it is instructive to see that under the assumption of constant force, these equations may be derived without calculus. Indeed, the same may be done for cases of constant jerk, snap, crackle, or pop, but it is more complicated and essentially useless, so we won't bother with it here.

Computational Model

Computational modelling of kinematics is generally done through iterative solution methods, such as those discussed for constant forces in Iterative Prediction, and for varying forces in Fundamentals of Iterative Prediction with Varying Force. However, when working with algebraic methods such as those discussed here one may also use analytic solution engines such as Mathematica (the more developed local form of WolframAlpha, which you may obtain through a GT software license) or Maple. A snippet of projectile motion code in Mathematica is included here for reference:

 (*First Cell*)
 (*Setup for a generic projectile motion problem*)
 launchspeed = 10
 launchangle = Pi/6
 vinit = launchspeed*{Cos[launchangle], Sin[launchangle], 0}
 launchpos = {0, 0, 0}
 yterminus = 0 
 g = 9.8

Naturally, one can edit these values to set up a different problem. The setup and the equation solution itself is separated into two cells (Mathematica has a cell notebook based structure) for cleanliness' sake.

 (*Second Cell*)
 (*Solving for the time of impact, then plugging that in to the original equations to find position in x and y *)
 T = Solve[-g*t^2/2 + vinit[[2]]*t + launchpos[[2]] == yterminus, t]
 finalpos = {(vinit[[1]]*t + launchpos[[1]]) /. T, (-g*t^2/2 + vinit[[2]]*t + launchpos[[2]]) /. T, 0}
 (* This gives 2 answers, the user must determine which is useful: if yinit  = 0, one will be at t=0, if yinit >0, one will be at t <0, if yinit < 0, both will be at t>0, so in the last case 
 you need to think about the situation*)

Analytic solution engines can be very useful, but one should make sure not so dependent upon them that one forgets how to do algebra!

Examples

1. (Simple)

An airplane begins at rest and accelerates down a runway at a constant [math]\displaystyle{ 3.20 \; \frac{m}{s^2} }[/math] for [math]\displaystyle{ 32.8 \; s }[/math] until is finally lifts off the ground. Determine a) the distance traveled before takeoff and b) the final velocity of the airplane.

Solution

a) The distance traveled can be determined with the following equation:

[math]\displaystyle{ \vec{r}_f = \frac{1}{2} \vec{a} \cdot t^2 + \vec{v}_i \cdot t + \vec{r}_i }[/math]

A one-dimensional version can be used because we are only concerned with motion along one axis:

[math]\displaystyle{ x_f = \frac{1}{2} a_x \cdot t^2 + v_{x, i} \cdot t + x_i }[/math]

The initial velocity of the plane is zero. If we define the origin to be the initial position of the plane, its initial position will be 0 as well, and the final position will be the same as distance traveled. Time t=0 is the instant the plane begins to accelerate.

[math]\displaystyle{ x_f = \frac{1}{2} (3.20 \; \frac{m}{s^2}) \cdot (32.8 \; s)^2 = 1720 \; m }[/math]

b) The final velocity can be determined with the following equation:

[math]\displaystyle{ \vec{v}_f = \vec{v}_i + \vec{a} \cdot t }[/math]

Again, let use use a one-dimensional version:

[math]\displaystyle{ v_{x, f} = v_{x, i} + a_x \cdot t }[/math]

[math]\displaystyle{ v_{x, f} = (3.20 \; \frac{m}{s^2}) \cdot (32.8 \; s) = 105 \; \frac{m}{s} }[/math]

The final velocity can alternatively be found using the equation [math]\displaystyle{ v_{x, f}^2 = v_{x, i}^2 + 2 a_x (x_f - x_i) }[/math]; all variables are known from the given information and the distance found above except [math]\displaystyle{ v_{x, f} }[/math].

2. (Medium)

A person throws a stone at an initial angle [math]\displaystyle{ \theta = 45^\circ }[/math] from the horizontal with an initial speed of [math]\displaystyle{ v =20 \; \frac{m}{s} }[/math]. The point of release of the stone is at a height d=2m above the ground. You may neglect air resistance.

a) How long does it take the stone to reach the highest point of its trajectory?

b) What was the maximum vertical displacement of the stone? Ignore air resistance.

c) What horizontal distance away does the stone land?

Let us call the origin the point on the ground directly below the point from which the stone is released, and let us define +y as upwards and +x as horizontally in the direction of the stone's travel. t=0 is the instant in time at which the stone is released.

Solution

a) At the highest point of the stone's trajectory, its vertical velocity is 0; the stone is moving entirely horizontally. Let us use this fact to determine how long the stone takes to get there, along with the following equation:

[math]\displaystyle{ v_{y, f} = v_{y, i} + a_y \cdot t }[/math]

[math]\displaystyle{ 0 = (20 \; \frac{m}{s})\cdot\sin(45^\circ) - (9.8 \; \frac{m}{s^2})\cdot t }[/math]

Solving for [math]\displaystyle{ t }[/math] yields [math]\displaystyle{ t = 1.44 \; s }[/math].

b) Now that we know how long it takes the stone to reach its highest point, we can use the following equation to find what that highest point its:

[math]\displaystyle{ y_f = \frac{1}{2} a_y \cdot t^2 + v_{y, i} \cdot t + y_i }[/math]

[math]\displaystyle{ y_f = \frac{1}{2} (-9.8 \; \frac{m}{s^2}) \cdot (1.44 \; s)^2 + (20 \; \frac{m}{s}) \sin(45^\circ) \cdot (1.44 \; s) + 2 \; m = 12.2 \; m }[/math]

The maximum height can alternatively be found using the equation [math]\displaystyle{ v_{y, f}^2 = v_{y, i}^2 + 2 a_y (y_f - y_i) }[/math]; all variables are known from the given information except [math]\displaystyle{ y_f }[/math].

c) The stone lands at height [math]\displaystyle{ y=0 }[/math], so let us use the following equation to see how long it takes the stone to get there. We need this information because then we know how much time the stone has to move in the +x direction before it hits the ground.

[math]\displaystyle{ y_f = \frac{1}{2} a_y \cdot t^2 + v_{y, i} \cdot t + y_i }[/math]

[math]\displaystyle{ 0 = \frac{1}{2} (-9.8 \; \frac{m}{s^2}) \cdot t^2 + (20 \; \frac{m}{s}) \sin(45^\circ) \cdot t + 2 \; m }[/math]

The quadratic equation must be used to solve for t:

[math]\displaystyle{ t = \frac{-b\pm\sqrt{b^2-4ac}}{2a} }[/math] (Note: here a, b, and c are the coefficients on the quadratic equation above. Do not confuse this "a" with the "a" signifying acceleration.)

[math]\displaystyle{ t = \frac{(-20 \; \frac{m}{s})\cdot\sin(45^\circ) \pm\sqrt{((20 \; \frac{m}{s}) \sin(45^\circ))^2-4 \cdot \frac{1}{2}(-9.8 \; \frac{m}{s^2}) \cdot 2}}{2 \cdot \frac{1}{2}(-9.8 \; \frac{m}{s^2})} }[/math]

[math]\displaystyle{ t = -.135\; s , 3.02 \;s }[/math]

There are two solutions because there are two times at which the ball is at the height y=0 using its parabolic trajectory. The first time, [math]\displaystyle{ t = -.135 }[/math]s, represents the time the ball would have been at ground height if it had been traveling along its parabolic path before time t=0. At this point in time, it would have been on its way up. The second time, [math]\displaystyle{ t = 3.02 }[/math]s, represents the time that the ball actually hits the ground on its way down. This is the time we are interested in.

Note that if the stone were to land at the same height from which it was launched, the time of flight would simply be twice the time it takes to reach the highest point. This is not the case for this problem because the stone is launched from 2m above the ground but lands on the ground.

Now we must use this time with a second kinematic equation involving the x coordinate of the ball to determine the horizontal distance it traveled while it was in the air. The equation we can use is:

[math]\displaystyle{ x_f = x_i + v_{x, avg} \cdot t }[/math]

[math]\displaystyle{ v_{x, avg} }[/math] is simply the initial horizontal velocity the ball was thrown with because no forces act on the ball in the x direction; [math]\displaystyle{ v_x }[/math] is constant.

[math]\displaystyle{ x_f = (20 \; \frac{m}{s}) \cos(45^\circ) \cdot 3.02 \; s = 42.73 }[/math]m

3. (Difficult)

A person is standing on a ladder holding a pail. The person releases the pail from rest at a height [math]\displaystyle{ h_1 }[/math] above the ground. A second person standing a horizontal distance [math]\displaystyle{ d }[/math] from the pail aims and throws a ball the instant the pail is released in order to hit the pail. The ball is thrown from a height [math]\displaystyle{ h_2 }[/math] above the ground with initial speed [math]\displaystyle{ v_0 }[/math]. Ignore air resistance.

a) At what angle [math]\displaystyle{ \Theta_0 }[/math] above the horizontal should the ball be thrown in order to hit the pail? Express your answer in terms of the other variables given.

b) How high above the ground does the collision occur?

Solution

For more practice with Kinematics, try the examples on the Projectile Motion page or the first few on the Acceleration page.

Connectedness

Application: Infrastructure/ Civil Engineering

The infrastructure on which vehicles travel must be built to accommodate their ability to speed up and slow down. For example, turn lanes should be longer where the speed limit is greater because a vehicle traveling at greater speeds needs more space to come to a stop. With knowledge of a vehicle's initial speed and ability to decelerate, kinematic equations can be used to determine the minimum length of a turn lane. Similarly, runways must be long enough to allow panes to reach takeoff speed. If the acceleration of a plane and the necessary speed for takeoff are known, kinematic equations can be used to calculate the minimum length of a runway.

Application: Accident Investigation

Imagine that a driver is moving down a straight road when suddenly another car backs out of a parking space onto the road in front of them. The driver slams on the brakes but does not have enough space to come to a stop and collides with the car backing out. Normally the driver of the parked vehicle would be considered at fault because you are responsible for checking behind you before you back out. However, an investigator may look at the marks left on the road by the skidding tires of the braking vehicle. Using the length of the marks and a kinematic equation, the investigator can determine the initial speed of the braking vehicle, and the driver may be held responsible for the accident if they were speeding.

Scenario: Projectile Motion

Because objects near the surface of the earth undergo constant acceleration, kinematic equations can be used to describe their motion.

History

Motion and geometry are some of the oldest fields of human study by virtue of their ubiquity. Kinematics being the glue that holds these concepts together, it is natural that it to is an extremely old subject. Ancient geometers understood a fair amount about the world empirically, identifying for example the nature of acceleration and creating models for the motions of the stars and planets. ^[2] However, their tools were very rudimentary, and their philosophies led them down many dead ends, such that it would be more than a millennium before substantial progress was made. Medieval scholars developed prototypes of coordinate geometry, and created the "Merton Rule," which is simply that in cases of constant acceleration equation (1) holds. ^[3] It was Galileo who helped extend these ideas to projectile motion, including the recognition that in the absence of air all objects would accelerate uniformly under gravity, and that projectiles follow parabolic arcs when given initial horizontal velocities. Newton's Principia Mathematics formalized these observations into mathematically rigorous laws, and his and Leibniz's calculus provided the tools for this analysis, with Leibniz making other contributions besides. ^[4] Finally, it was Ampère who coined the term kinematics to describe this branch of physics. ^[5]

[2] ttps://ir.uiowa.edu/cgi/viewcontent.cgi?article=1014&context=iihr_monograph_series

[3] ttps://amsi.org.au/ESA_Senior_Years/SeniorTopic3/3i/3i_4history_1.html

[4] ttp://home.iitk.ac.in/~ag/ESO202/Truesdell1.pdf

[5] Macagno

[1]

[2]

[3]

[4]

[5]

Kinematics

Contents

The Main Idea

Quantities of Kinematics

A Mathematical Model

The Kinematic Equations

Derivation

Computational Model

Examples

1. (Simple)

2. (Medium)

3. (Difficult)

Connectedness

Application: Infrastructure/ Civil Engineering

Application: Accident Investigation

Scenario: Projectile Motion

History

See also

Further reading

External Links

References

Navigation menu