Newton's Second Law: the Momentum Principle

From Physics Book
Jump to navigation Jump to search

Claimed by Arayna Saxena, Fall 2024


This page describes Newton's second law of motion, also known as the momentum principle, which relates net force to the change in Linear Momentum. This principle is used to predict the effects of forces on the motion of objects.

Newton's Second Law is fundamental to understanding motion and lays the groundwork for classical mechanics and modern physics applications.For instance, understanding the force needed to accelerate a car, or how a rocket changes velocity in space, relies on this principle.

The Main Idea

Newton's second law of motion, also known as the momentum principle, explains how forces cause the momentum of a system to change over time.

Linear Momentum ([math]\displaystyle{ \vec{p} }[/math]) is the product of an object's mass ([math]\displaystyle{ m }[/math]) and velocity ([math]\displaystyle{ \vec{v} }[/math]):

[math]\displaystyle{ \vec{p} = m\vec{v} }[/math].

Net Force ([math]\displaystyle{ \vec{F}_{net} }[/math]) is the total force acting on a system.

The principle states that:

[math]\displaystyle{ \vec{F}{net} = \frac{d\vec{p}{system}}{dt} }[/math]

where:

[math]\displaystyle{ \vec{p} }[/math] is the Linear Momentum of a system, [math]\displaystyle{ \vec{F}_{net} }[/math] is the external Net Force acting on the system from its surroundings, and [math]\displaystyle{ t }[/math] is time. Often, the system in question consists of a single particle whose motion we want to predict, although the law is also true for systems of particles and non-particle distributions of mass, such as disks. Note that both force and momentum are vector quantities, and that the change in momentum as a result of a force will always be in the direction of that force.

These examples illustrate how the momentum principle applies in different scenarios:

  1. If a particle travels in a straight line at a constant speed, its momentum is constant, so there is no net force acting on the particle.
  2. If a particle travels in a straight line while speeding up, its momentum is increasing, so there must be a net force acting in the same direction as the particle's momentum.
  3. If a particle travels in a straight line while slowing down, its momentum is decreasing, so there must be a net force acting in the opposite direction as the particle's momentum.
  4. If a particle travels along a curving path, its momentum changes direction, and a force not parallel to the object's momentum must be acting on it.

The momentum principle has no derivation, as it is considered the definition of force. The metric unit most commonly used for force is the Newton.


A Mathematical Model

The momentum principle states that:

[math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math]

where [math]\displaystyle{ \vec{p} }[/math] is the momentum of the system. Momentum is defined as:

[math]\displaystyle{ \vec{p} = m\vec{v} }[/math]

Applying the product rule to the time derivative of momentum:

[math]\displaystyle{ \frac{d\vec{p}}{dt} = m\frac{d\vec{v}}{dt} + \vec{v}\frac{dm}{dt} }[/math]

For systems where the mass of the particle or system is constant over time (e.g., most classical mechanics problems), the second term [math]\displaystyle{ \vec{v}\frac{dm}{dt} }[/math] becomes zero. This simplifies the momentum principle to:

[math]\displaystyle{ \vec{F}{net} = m\frac{d\vec{v}}{dt} }[/math] or equivalently [math]\displaystyle{ \vec{F}{net} = m\vec{a} }[/math],

which is the more familiar form of Newton's Second Law. However, the general form [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] is preferred in many scenarios for the following reasons:

  1. Changing Mass Systems: When the mass of a particle or system changes with time (e.g., a rocket expelling fuel or a snowball gaining mass as it rolls downhill), the term [math]\displaystyle{ \vec{v}\frac{dm}{dt} }[/math] is no longer zero. In such cases, [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] is inaccurate, but the general form [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] correctly accounts for these changes.
  2. Relativistic Speeds: As a particle approaches the speed of light, classical mechanics fails to accurately describe the motion, and relativistic momentum must be used: [math]\displaystyle{ \vec{p} = \frac{m\vec{v}}{\sqrt{1 - \frac{v^2}{c^2}}} }[/math], where [math]\displaystyle{ c }[/math] is the speed of light. In these cases, [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] is invalid, while [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] remains accurate when relativistic momentum is substituted.
  3. Rotational Analogues: The form [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] provides a direct analogy to rotational motion, where **torque** ([math]\displaystyle{ \vec{\tau} }[/math]) is defined as the rate of change of **angular momentum** ([math]\displaystyle{ \vec{L} }[/math]): [math]\displaystyle{ \vec{\tau} = \frac{d\vec{L}}{dt} }[/math] Here: [math]\displaystyle{ \vec{\tau} }[/math] is the torque applied to a system, [math]\displaystyle{ \vec{L} }[/math] is the angular momentum ([math]\displaystyle{ \vec{L} = \vec{r} \times \vec{p} }[/math], where [math]\displaystyle{ \vec{r} }[/math] is the position vector). This analogy is valuable because many principles in linear motion (e.g., momentum, force) extend directly to rotational dynamics (e.g., angular momentum, torque). By learning linear dynamics in the general form [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math], students can more easily understand and apply analogous principles to rotational systems.

Despite these advantages, the relation [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] is often sufficient for systems with constant mass moving at non-relativistic speeds. It is especially useful when combined with kinematic equations that utilize acceleration [math]\displaystyle{ \vec{a} }[/math] to predict motion.

Impulse and Momentum

The momentum principle also establishes the relationship between Impulse and Momentum:

[math]\displaystyle{ \vec{F}_{net} \Delta t = \Delta \vec{p} }[/math]

Here, [math]\displaystyle{ \vec{F}_{net} \Delta t }[/math] is the impulse applied to a system, and [math]\displaystyle{ \Delta \vec{p} }[/math] is the resulting change in momentum. This relationship is particularly useful for analyzing systems where forces act over short time intervals, such as collisions in sports or car crashes.

Conservation of Momentum

When the net external force on a system is zero (i.e., the system is isolated or closed), the momentum principle simplifies to:

[math]\displaystyle{ \frac{d\vec{p}}{dt} = 0 }[/math]

This implies that the system's total momentum remains constant:

[math]\displaystyle{ \vec{p}{initial} = \vec{p}{final} }[/math]

This principle is known as Conservation of Momentum, and it underpins many physical phenomena, including:

Elastic and inelastic collisions. Rocket propulsion in space, where the expelled fuel and rocket system together conserve momentum. By understanding these fundamental relationships, we gain insight into how forces interact with systems to produce motion and momentum changes under various conditions.

A Computational Model

The relationship between net force and change in momentum can be computationally modeled using the momentum update formula:

[math]\displaystyle{ p_2 = p_1 + F_{net} \cdot \Delta t }[/math].

This is a rewriting of [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math], where mass is assumed to be constant.

Steps in the Computational Model Define Momentum: Momentum is calculated as the object’s mass multiplied by its velocity in the initial conditions. Iterative Prediction: For each time step: Update [math]\displaystyle{ F_{net} }[/math] by summing all possible forces acting on the object during the simulation. Use the momentum principle to update the momentum: [math]\displaystyle{ p = p + F_{net} \cdot \Delta t }[/math]. Calculate the velocity from momentum: [math]\displaystyle{ \vec{v} = \frac{\vec{p}}{m} }[/math]. Update the position: [math]\displaystyle{ \vec{r}_2 = \vec{r}_1 + \vec{v} \cdot \Delta t }[/math].


Model Description

This simulation models the motion of a falling object under the force of gravity, using the momentum principle. The object's position and velocity are updated iteratively, and the output is visualized in real-time using graphs and arrows representing forces.

Key Features

Interactive Visualization: The simulation shows the position, velocity, and force vectors in real time. Graphing Tools: Position and velocity vs. time graphs are plotted, enabling analysis of motion dynamics. Customizability: Parameters like mass, initial position, initial velocity, and time step ([math]\displaystyle{ \Delta t }[/math]) can be adjusted for different scenarios. You can interact with the simulation on GlowScript here:


https://www.glowscript.org/#/user/Arayna%5fSaxena/folder/MyPrograms/program/Lab2onlygravity

Examples

1. (Simple)

At [math]\displaystyle{ t = 0 }[/math], a 6 kg particle is released from rest, and a constant 18 N force begins acting on it. How far has the particle moved after 4 seconds?

To solve this problem, we use [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math], which is a simpler form of Newton's Second Law in scenarios with constant mass and non-relativistic speeds. This allows us to calculate the acceleration first and then use kinematic equations to determine the displacement.

Step 1: Calculate Acceleration

Rearranging [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math], we find:

[math]\displaystyle{ \vec{a} = \frac{\vec{F}_{net}}{m} }[/math]

Substitute the given values:

[math]\displaystyle{ a = \frac{18}{6} = 3 , \text{m/s}^2 }[/math]

Step 2: Apply Kinematic Equation

The displacement can be calculated using the kinematic equation:

[math]\displaystyle{ x_f = \frac{1}{2}at^2 + v_it + x_i }[/math]

Since the particle starts from rest ([math]\displaystyle{ v_i = 0 }[/math]) and at the origin ([math]\displaystyle{ x_i = 0 }[/math]), the equation simplifies to:

[math]\displaystyle{ x_f = \frac{1}{2}a t^2 }[/math]

Substitute the values for [math]\displaystyle{ a }[/math] and [math]\displaystyle{ t }[/math]:

[math]\displaystyle{ x_f = \frac{1}{2}(3)(4^2) }[/math]

[math]\displaystyle{ x_f = \frac{1}{2}(3)(16) = 24 , \text{m} }[/math]

Final Answer

The particle has moved a total distance of [math]\displaystyle{ 24 , \text{m} }[/math] after 4 seconds.

2. (Middling)

A 1.2 kg cart moving with an initial velocity of [math]\displaystyle{ v_i = 5 , \text{m/s} }[/math] collides with a stationary 0.8 kg cart on a frictionless track. After the collision, the two carts stick together. Determine their final velocity after the collision, assuming it is totally inelastic. Additionally, calculate the energy lost during the collision.

Inelastic Collision

In a perfectly inelastic collision, the objects stick together after impact. While kinetic energy is not conserved, momentum is always conserved.

The momentum principle states:

[math]\displaystyle{ \vec{p}{initial} = \vec{p}{final} }[/math]

Step 1: Write the Momentum Conservation Equation

The initial momentum is:

[math]\displaystyle{ \vec{p}{initial} = m_1 v{i1} + m_2 v_{i2} }[/math]

The final momentum is:

[math]\displaystyle{ \vec{p}_{final} = (m_1 + m_2) v_f }[/math]

Equating initial and final momentum:

[math]\displaystyle{ m_1 v_{i1} + m_2 v_{i2} = (m_1 + m_2) v_f }[/math]

Step 2: Solve for Final Velocity

Substitute the given values:

[math]\displaystyle{ m_1 = 1.2 , \text{kg} }[/math], [math]\displaystyle{ v_{i1} = 5 , \text{m/s} }[/math] [math]\displaystyle{ m_2 = 0.8 , \text{kg} }[/math], [math]\displaystyle{ v_{i2} = 0 , \text{m/s} }[/math] [math]\displaystyle{ (1.2)(5) + (0.8)(0) = (1.2 + 0.8) v_f }[/math]

[math]\displaystyle{ 6 = 2 v_f }[/math]

[math]\displaystyle{ v_f = 3 , \text{m/s} }[/math]

The final velocity of the combined system is [math]\displaystyle{ 3 , \text{m/s} }[/math].

Step 3: Calculate Kinetic Energy Before and After the Collision

Initial kinetic energy:

[math]\displaystyle{ KE_{initial} = \frac{1}{2} m_1 v_{i1}^2 + \frac{1}{2} m_2 v_{i2}^2 }[/math]

[math]\displaystyle{ KE_{initial} = \frac{1}{2}(1.2)(5^2) + \frac{1}{2}(0.8)(0^2) }[/math]

[math]\displaystyle{ KE_{initial} = 15 , \text{J} }[/math]

Final kinetic energy:

[math]\displaystyle{ KE_{final} = \frac{1}{2}(m_1 + m_2)v_f^2 }[/math]

[math]\displaystyle{ KE_{final} = \frac{1}{2}(2)(3^2) }[/math]

[math]\displaystyle{ KE_{final} = 9 , \text{J} }[/math]

Step 4: Calculate Energy Lost

Energy lost:

[math]\displaystyle{ \Delta KE = KE_{initial} - KE_{final} }[/math]

[math]\displaystyle{ \Delta KE = 15 - 9 }[/math]

[math]\displaystyle{ \Delta KE = 6 , \text{J} }[/math]

Final Answer

The final velocity of the combined system is [math]\displaystyle{ 3 , \text{m/s} }[/math]. The total energy lost during the collision is [math]\displaystyle{ 6 , \text{J} }[/math].

3. (Difficult)

A rocket ship of mass [math]\displaystyle{ M }[/math] and initial speed [math]\displaystyle{ v }[/math] moves through a stationary dust cloud with a particle density of [math]\displaystyle{ N }[/math] (particles per unit volume). Each dust particle has a mass [math]\displaystyle{ m }[/math], and the rocket has a circular cross-sectional radius of [math]\displaystyle{ R }[/math]. The sticky surface of the rocket collects the dust particles, increasing its mass as it travels. To maintain a constant speed, determine the thrust force required by the rocket’s engines.

Step 1: Rate of Mass Accumulation

As the rocket moves through the dust cloud, it accumulates mass at a rate proportional to its velocity and the density of the dust. The rate of mass increase ([math]\displaystyle{ \frac{dm}{dt} }[/math]) is determined as follows:

The rocket sweeps out a cylindrical volume of dust per unit time: [math]\displaystyle{ \text{Volume swept per second} = \pi R^2 v }[/math] The mass of dust particles in this volume is: [math]\displaystyle{ \text{Mass swept per second} = (\text{Density of particles}) \cdot (\text{Mass per particle}) \cdot (\text{Volume swept}) }[/math] Substituting: [math]\displaystyle{ \frac{dm}{dt} = N m \pi R^2 v }[/math]

Step 2: Momentum Conservation

The momentum principle states that the net force acting on the system is equal to the rate of change of momentum:

[math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math]

The total momentum of the rocket system is: [math]\displaystyle{ p = (M + m_{\text{dust}}) v }[/math]

Where:

[math]\displaystyle{ M }[/math] is the initial mass of the rocket, [math]\displaystyle{ m_{\text{dust}} }[/math] is the mass of the accumulated dust, [math]\displaystyle{ v }[/math] is the constant velocity (no change in [math]\displaystyle{ v }[/math] since the rocket maintains its speed). Since [math]\displaystyle{ v }[/math] is constant, the rate of change of momentum is due only to the accumulation of mass:

[math]\displaystyle{ \frac{d\vec{p}}{dt} = v \frac{dm}{dt} }[/math]

Substitute [math]\displaystyle{ \frac{dm}{dt} }[/math] from Step 1:

[math]\displaystyle{ \frac{d\vec{p}}{dt} = v (N m \pi R^2 v) }[/math]

[math]\displaystyle{ \frac{d\vec{p}}{dt} = N m \pi R^2 v^2 }[/math]

Step 3: Thrust Force Required

To maintain a constant velocity, the rocket’s thrusters must exert a force equal and opposite to the force exerted by the accumulating dust:

[math]\displaystyle{ F_{\text{thrust}} = \frac{d\vec{p}}{dt} }[/math]

Thus:

[math]\displaystyle{ F_{\text{thrust}} = N m \pi R^2 v^2 }[/math]

Final Answer The thrust force required to maintain a constant speed is:

[math]\displaystyle{ F_{\text{thrust}} = N m \pi R^2 v^2 }[/math]

4. (Difficult)

A particle of mass [math]\displaystyle{ m }[/math] and speed [math]\displaystyle{ v }[/math] moves in a circular path with an angular frequency [math]\displaystyle{ \Omega }[/math]. Using the momentum principle, demonstrate the following:

a) A nonzero net force is acting on the particle.

b) The magnitude of this force is [math]\displaystyle{ F = mv\Omega }[/math].

c) The direction of the force is inwards, towards the center of the circle.

a) Nonzero Net Force Acting on the Particle

The particle moves in a circular path, which means its velocity vector is constantly changing direction even though its speed remains constant. The momentum vector [math]\displaystyle{ \vec{p} = m\vec{v} }[/math] changes as the direction of [math]\displaystyle{ \vec{v} }[/math] changes, which implies that:

[math]\displaystyle{ \frac{d\vec{p}}{dt} \neq 0 }[/math]

From Newton's Second Law, we know that:

[math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math]

Since [math]\displaystyle{ \vec{p} }[/math] changes due to the particle's changing velocity direction, a nonzero net force must act on the particle. This force is responsible for continuously changing the direction of the particle's velocity, keeping it in circular motion.

For a particle of constant mass, the only way [math]\displaystyle{ \vec{F}_{net} = 0 }[/math] is if the particle is at rest or traveling in a straight line at constant speed, neither of which applies to circular motion.

b) Magnitude of the Force

To determine the magnitude of the net force, consider the centripetal force required to keep the particle moving in a circle. The centripetal force ensures that the particle maintains its circular path by continuously pulling it towards the center.

Angular Frequency Relationship: The angular frequency [math]\displaystyle{ \Omega }[/math] is related to the particle's speed and the radius of the circular path: [math]\displaystyle{ v = \Omega R }[/math] Substituting for [math]\displaystyle{ R }[/math] gives: [math]\displaystyle{ R = \frac{v}{\Omega} }[/math] Centripetal Acceleration: The centripetal acceleration is: [math]\displaystyle{ a_c = \frac{v^2}{R} }[/math] Substituting [math]\displaystyle{ R = \frac{v}{\Omega} }[/math]: [math]\displaystyle{ a_c = v \Omega }[/math] Force Magnitude: Using Newton's Second Law: [math]\displaystyle{ F = ma_c }[/math] Substituting for [math]\displaystyle{ a_c }[/math]: [math]\displaystyle{ F = m v \Omega }[/math] Thus, the magnitude of the force is:

[math]\displaystyle{ F = mv\Omega }[/math]

c) Direction of the Force

The direction of the net force acting on the particle is always towards the center of the circular path. This force is often referred to as the centripetal force.

Momentum Vector Analysis: The momentum vector [math]\displaystyle{ \vec{p} = m\vec{v} }[/math] is tangential to the circular path and changes direction as the particle moves. The change in momentum [math]\displaystyle{ d\vec{p} }[/math] points towards the center of the circle, as shown in the diagram below:


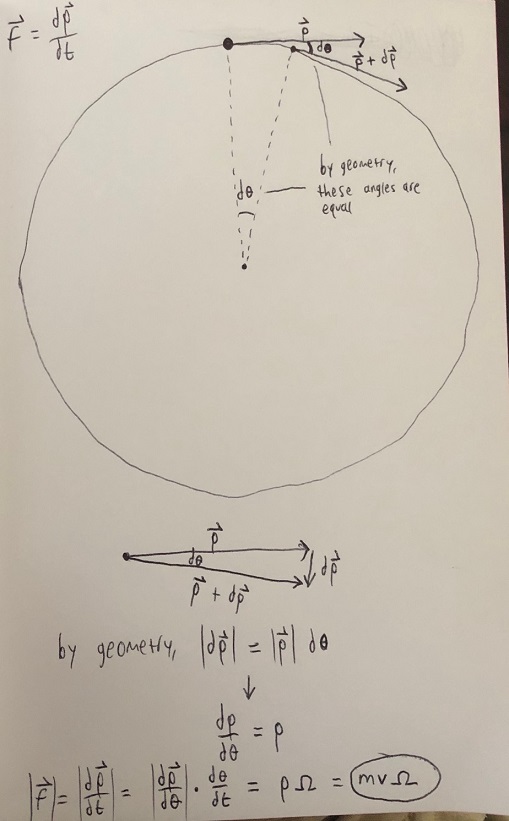
Direction Explanation: At any point on the circular path, the force responsible for changing [math]\displaystyle{ \vec{p} }[/math] acts perpendicular to the velocity vector and points radially inwards. For example, if the particle is at the top of the circle moving to the right, the force vector points downward towards the center. This is consistent throughout the motion. Thus, the force direction is always radially inward, ensuring the particle remains in circular motion.

Final Summary a) A nonzero net force acts on the particle because its momentum changes direction over time.

b) The magnitude of this force is:

[math]\displaystyle{ F = mv\Omega }[/math]

c) The force always points inwards towards the center of the circle, perpendicular to the particle's instantaneous velocity.

Connectedness

Newton's Second Law is a universal principle that connects forces, momentum, and motion. It applies to any scenario where forces are present, causing changes in a system's momentum. These applications span countless fields, from everyday situations to cutting-edge technologies. Below are examples that highlight the versatility and importance of this law.

Scenario: Bungee Jump

A bungee jump is a dynamic example of Newton's Second Law in action. Initially, the jumper accelerates downward due to gravity. As the cord stretches and becomes taut, it exerts an upward elastic restoring force, which increases with the cord's extension.

Force Interaction:

At maximum stretch, the cord's force becomes greater than the gravitational force, causing a net upward force. This net upward force reduces the jumper's downward velocity and eventually reverses their motion. Momentum Changes: The jumper's momentum transitions from downward to upward as the net force changes direction. When the cord slackens, gravity again becomes the dominant force, and the jumper accelerates downward, repeating the cycle. Energy Considerations: The gravitational potential energy decreases as the jumper falls and is converted into elastic potential energy in the cord. At the lowest point, the system stores maximum elastic potential energy, which transforms back into kinetic energy as the jumper rebounds. This interplay of forces and momentum illustrates the principle of force-driven motion and how Newton's Second Law governs complex oscillatory systems like a bungee jump.

Application: Automobile Industry

Newton's Second Law is critical in automotive design, as it governs vehicle motion under forces such as engine thrust, braking, and turning.

Acceleration and Braking: When a car accelerates, the engine provides a forward force that overcomes friction and air resistance, resulting in an increase in momentum. Braking applies a backward force, reducing the car's momentum and eventually bringing it to a stop. Turning Forces: During a turn, frictional forces between the tires and road provide the centripetal force necessary to change the car's direction. Without sufficient friction, the car would skid outward due to inertia. Role of Static Friction: The tires rely on static friction, not kinetic friction, to grip the road. The maximum static friction force determines how much the car can accelerate or turn without slipping. This force is influenced by factors such as tire material, tread design, and the car’s weight. Design Implications: Automotive engineers optimize tire materials, suspension systems, and aerodynamics to maximize the forces that can be safely exerted. Electric vehicles, for example, use precise torque control to distribute forces efficiently across tires, enhancing both acceleration and braking. The application of Newton’s Second Law in automotive design ensures vehicles operate safely and efficiently under various forces.

Additional Examples of Connectedness

Rocket Propulsion:

Rockets eject fuel at high velocity, creating a thrust force due to the conservation of momentum. This force propels the rocket forward and is directly tied to Newton's Second Law.

Sports Dynamics:

In sports, athletes use force to change the momentum of objects like balls or their own bodies. For example, a soccer kick applies a net force that accelerates the ball, and the force direction determines its trajectory.

Space Exploration:

Spacecraft rely on Newton’s Second Law for trajectory corrections, where even small thrusters provide precise changes in momentum to adjust the spacecraft's path.

Biomechanics:

Human motion, such as running or jumping, is governed by forces exerted by muscles that cause changes in the body's momentum. Understanding these forces helps in injury prevention and optimizing athletic performance.

History

In his groundbreaking 1687 work Philosophiæ Naturalis Principia Mathematica (commonly referred to as Principia Mathematica), Isaac Newton (1643–1727) introduced his three laws of motion. While the first and third laws were inspired by the work of earlier scientists, such as Galileo Galilei and René Descartes, Newton's Second Law was an entirely original contribution to the understanding of dynamics. This law is considered one of the cornerstones of classical mechanics.

The Original Statement

The Second Law was originally written in Latin as:

“Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.” This was closely translated in Andrew Motte's 1729 English edition of Principia Mathematica as:

“Law II: The alteration of motion is ever proportional to the motive force impress'd; and is made in the direction of the right line in which that force is impress'd.” In modern terms, this can be interpreted as:

The rate of change of momentum of a body is proportional to the net force acting on it. The direction of the change in momentum is the same as the direction of the applied force. Defining Force This law was the first rigorous definition of force, linking it quantitatively to changes in momentum. Newton’s formulation unified and clarified many previous ideas about motion and force, enabling scientists to make precise predictions about physical systems.

Legacy

Newton's contributions to the study of forces have had a lasting impact on physics and engineering. The unit of force in the International System of Units (SI), the Newton (N), is named in his honor. One Newton is defined as the force required to accelerate a one-kilogram mass by one meter per second squared:

[math]\displaystyle{ 1 , \text{N} = 1 , \text{kg} \cdot \text{m/s}^2 }[/math]

Broader Implications

Newton's Second Law not only revolutionized mechanics but also laid the foundation for other fields of physics. It enabled the development of:

Orbital Mechanics: Used to predict the motion of planets, moons, and artificial satellites. Engineering Design: Governs the behavior of structures and machines under forces. Modern Dynamics: Serves as a precursor to advanced theories, such as Lagrangian and Hamiltonian mechanics. Newton's Principia Mathematica remains a seminal text in the history of science, and the Second Law continues to be a fundamental tool for understanding and modeling the physical world.

See also

Further reading

RANKINE, William John Macquorn, and Edward Fisher BAMBER. A Mechanical Text Book. 1873. Print.

External links

  1. nhttp://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/Part_III/Chapter_3_Stress_Mass_Momentum/Stress_Balance_Principles_02_The_Momentum_Principles.pdf
  2. http://acme.highpoint.edu/~atitus/phy221/lecture-notes/2-2-momentum-principle.pdf
  3. https://www.khanacademy.org/science/physics/forces-newtons-laws/newtons-laws-of-motion/v/newton-s-second-law-of-motion
  4. https://www.khanacademy.org/science/physics/forces-newtons-laws/newtons-laws-of-motion/v/more-on-newtons-second-law
  5. https://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion3.htm
  6. https://www.livescience.com/46560-newton-second-law.html

References

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Newton%27s_Second_Law:_the_Momentum_Principle&oldid=46796"