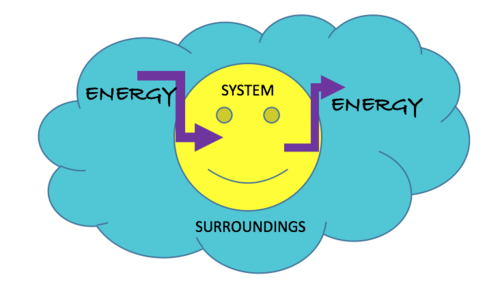
System & Surroundings
Main Idea
When it comes to energy, choosing what is the system versus what is the surroundings has profound effects on what needs to be accounted for when solving for various values/variables. Choosing certain objects to be a part of the system rather than the surroundings can have an extreme effect on the outcome of said variables, especially when the surroundings do a fairly large amount of work on the system.
By definition, a system is a specific part of the universe that we choose to study and analyze, while the surroundings are everything else that 'surrounds,' and typically has a significant effect on, the system. This page will analyze how different choices of systems can affect the components of the Energy Principle when relating it to the system.
When deciding what to choose as your system versus your surroundings, it is important to look at your scenario from a very generalized point of view. For the system, look for a group or collections of parts or objects that are interacting and closed within what is called a system boundary. The system boundary helps to distinguish the system as one entity rather than many things moving at once.
Mathematical Model
The mathematical model related to choice of system focuses on the The Energy Principle.
Types of Energy Systems
- 1. An Open Energy System
- An Open Energy System is subject to changes in it's internal energy as a result of energy transfers between the system and its surroundings. These transfers could be either into the system or out of the system and as a result [math]\displaystyle{ \mathbf{\vartriangle}E_{system} }[/math] could be negative or positive. The total energy of an open system is therefore not constant. For instance, when you boil rice in an open saucepan on a stove, energy is being transferred to the surroundings in the form of steam. The open saucepan is an example of an open system, and as steam escapes to the surroundings there is loss of thermal energy from the system (remember [math]\displaystyle{ \mathbf{\vartriangle}E_{system} }[/math] is not constant).
- 2. A Closed Energy System
- A Closed Energy System is not subject to changes in its internal energy. Therefore:
- [math]\displaystyle{ \Delta E_{system} = 0 }[/math]
- Although energy transfers between the system and surroundings exist, the amount of energy inflow is equal to the amount of energy outflow, and therefore the net change in energy is equal to zero. An example of a closed system could be a thermos flask. If ice cubes and boiling water are placed into the thermos at the same time, there would an increase in the energy of the ice cubes and an equal decrease in the energy of the boiling water, resulting in the net change of energy to be zero. However, it is important to note that no system can be perfectly closed, and there would be negligible leakage of energy to the surroundings form the thermos flask as it is not perfectly insulated.
The Energy Principle
- To first understand the impact of the choice of system, it is best to fully understand the Energy Principle. The Energy Principle is based on the fact that energy is a conserved quantity in the universe, meaning that it cannot be created nor destroyed, only transferred. This definition of the conservation of energy gives us the equation:
- [math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]
- The following image best illustrates the idea that since energy is a conserved quantity, systems may only gain/lose energy if the surroundings lose/gain that same amount of energy.
- The Energy Principle can then be rearranged by using the fact that the change in energy of a specific system is equal to the work done on the system by the surroundings, or:
- [math]\displaystyle{ \Delta E_{system} = W_{surroundings} }[/math], where
- [math]\displaystyle{ \Delta E_{system} = E_f - E_i }[/math] (The final energy of the system minus the initial energy of the system)
- This facts gives:
- [math]\displaystyle{ E_f = E_i + W_{surroundings} }[/math]
- The above equation is what we will primarily use when accounting for all of the energy terms when the choice of system/surroundings changes.
Computational Model
Using VPython, we can analyze a number of open and closed energy systems. The following code will follow the energy and thus the motion of a sphere attached to a pendulum in a closed system situation, as well as an open system situation. The length of the rope is [math]\displaystyle{ L = 1 \ \text{m} }[/math], the mass of the sphere is [math]\displaystyle{ m = 0.5 \ \text{kg} }[/math], the initial velocity of the sphere is [math]\displaystyle{ \mathbf{v}_0 = \mathbf{0} \ \frac{m}{s} }[/math], and the initial angle to the vertical is [math]\displaystyle{ \theta_0 = 30^\text{o} }[/math]. In the open energy system, an air resistance force will do work against the sphere's motion, given by the following: [math]\displaystyle{ F_{air} = 0.3v^2 }[/math], where [math]\displaystyle{ v }[/math] is the speed of the sphere.
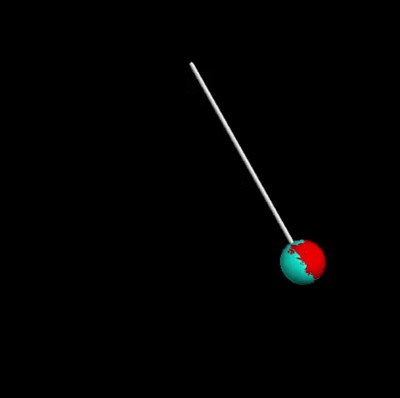
from __future__ import division
from visual import *
from visual.graph import *
scene.center = (0,-0.5,0)
top = sphere(pos = vector(0,0,0), radius = 0.01)
LENGTH OF STRING
L = 1
INITIAL ANGLE
theta = 30 * pi/180
THE GRAVITATIONAL CONSTANT IN SCALAR FORM
gg = 9.8
THE GRAVITATIONAL CONSTANT IN VECTOR FORM
g = vector(0,-9.8,0)
balla = sphere(pos = L*vector(sin(theta), -cos(theta),0), radius = 0.1, color = color.cyan)
balla.m = 0.5
balla.p = vector(0,0,0)
traila = curve(color = color.yellow)
stringa = cylinder(pos = top.pos, axis = (balla.pos - top.pos), radius = 0.01)
ballb = sphere(pos = L*vector(sin(theta), -cos(theta),0), radius = 0.1, color = color.red)
ballb.m = 0.5
ballb.p = vector(0,0,0)
trailb = curve(color = color.green)
stringb = cylinder(pos = top.pos, axis = (ballb.pos - top.pos), radius = 0.01)
t = 0
dt = 0.001
while t < 10:
rate(1000)
#Calculate the vector from balla to the top
ra = top.pos - balla.pos
#Fnet is graviational plus tension
#v is the scalar velocity
va = mag(balla.p)/balla.m
#calculate the magnitude of the ball's acceleration
balla.a = (va**2)/L
#theta is the angular position of the ball
thetaa = atan(balla.pos.x/(-balla.pos.y))
#calculate the vector tension force
Ta = (balla.m * gg * cos(thetaa) + balla.m * balla.a) * norm(ra)
#calculate the net force
Fneta = balla.m * g + Ta
#update momentum of ball
balla.p = balla.p + Fneta * dt
#update position of ball
balla.pos = balla.pos + balla.p * dt / balla.m
#update the string
stringa.axis = balla.pos - top.pos
traila.append(balla.pos)
Ea = balla.m * gg * balla.pos.y + (1/2) * balla.m * (mag(balla.p)/balla.m)**2
if t > 9.5:
print(Ea)
rb = top.pos - ballb.pos
#Fnet is graviational plus tension minus the air resistance
#v is the scalar velocity
vb = mag(ballb.p)/ballb.m
#calculate the magnitude of the ball's acceleration
ballb.a = (vb**2)/L
#theta is the angular position of the ball
thetab = atan(ballb.pos.x/(-ballb.pos.y))
#calculate the vector tension force
Tb = (ballb.m * gg * cos(thetab) + ballb.m * ballb.a) * norm(rb)
#calculate air resistance
F_air = 0.3 * (vb)**2 * norm(ballb.p)
#calculate the net force
Fnetb = ballb.m * g + Tb - F_air
#update momentum of ball
ballb.p = ballb.p + Fnetb * dt
#update position of ball
ballb.pos = ballb.pos + ballb.p * dt / ballb.m
#update the string
stringb.axis = ballb.pos - top.pos
trailb.append(ballb.pos)
Eb = ballb.m * gg * ballb.pos.y + (1/2) * ballb.m * (mag(ballb.p)/ballb.m)**2
if t > 9.9:
print(Eb)
t = t+dt
Examples
Although physical results are always consistent, choosing different objects as the system changes the form of the energy equation and which energy terms must be included in order to calculate accurate values for unknowns.
In the following examples, fairly complex systems will be analyzed in several different ways. Each of these will show a different choice of system and surroundings and how this effects the Energy Principle.
Simple
A man of mass [math]\displaystyle{ M }[/math] is lifting his child of mass [math]\displaystyle{ m }[/math] over his head a distance [math]\displaystyle{ d }[/math] with a constant force [math]\displaystyle{ F }[/math]. When the child is a distance [math]\displaystyle{ d }[/math] over the man's head, the child is moving with a constant velocity [math]\displaystyle{ v_f }[/math].

- a) Create an expression for the change in the energy of the man ([math]\displaystyle{ \mathbf{\vartriangle}E_{man} }[/math]), disregarding thermal or frictional energy losses, using the Energy Principle and a choice of system where the man, child, and Earth are all part of the system. All of the surroundings do no significant work on the system, and the system does no work on the surroundings.
- We know in general that the change in energy of the system and its surroundings is always [math]\displaystyle{ 0 }[/math]:
- [math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]
- or:
- [math]\displaystyle{ (E_{system_{f}} - E_{system_{i}}) + (E_{surroundings_{f}} - E_{surroundings_{i}}) = 0 }[/math]
- We know the surroundings are considered negligible in this question since they do no work on the system, as well as have no work done to them:
- [math]\displaystyle{ E_{system_{i}} = E_{system_{f}} }[/math]
- Using:
- [math]\displaystyle{ E = U + K }[/math]
- We get that:
- [math]\displaystyle{ U_{system_{i}} + K_{system_{i}} = U_{system_{f}} + K_{system_{f}} }[/math]
- Which is equivalent to:
- [math]\displaystyle{ (U_{child_{i}} + U_{man_{i}} + U_{Earth_{i}}) + (K_{child_{i}} + K_{man_{i}} + K_{Earth_{i}}) = (U_{child_{f}} + U_{man_{f}} + U_{Earth_{f}}) + (K_{child_{f}} + K_{man_{f}} + K_{Earth_{f}}) }[/math]
- Therefore:
- [math]\displaystyle{ (U_{man_{f}} + K_{man_{f}}) - (U_{man_{i}} + K_{man_{i}}) = (U_{child_{i}} - U_{child_{f}}) + (U_{Earth_{i}} - U_{Earth_{f}}) + (K_{child_{i}} - K_{child_{f}}) + (K_{Earth_{i}} - K_{Earth_{f}}) }[/math]
- We can manipulate this into:
- [math]\displaystyle{ \Delta E_{man} = -\Delta U_{child} - \Delta U_{Earth} - \Delta K_{child} -\Delta K_{Earth} }[/math]
- Since the child and the man are near the surface of the Earth, using [math]\displaystyle{ mgh }[/math] as the gravitational potential energy for them is acceptable. Also, the Earth has no significant movement from this reference frame, since the child and man are so much less massive than it, meaning its change in gravitational potential energy is negligible and velocity is 0:
- [math]\displaystyle{ \Delta E_{man} = - mg(d-0) - 0 - \frac{1}{2}m({v_f}^2 - 0) - 0 }[/math]
- Simplifying gives a final answer:
- [math]\displaystyle{ \Delta E_{man} = - \left(mgd + \frac{1}{2}m{v_f}^2\right) }[/math]
- b) Create an expression for the final velocity of the child ([math]\displaystyle{ v_f }[/math]) , using the Energy Principle and the child as the system, and the man and the Earth doing significant work on the system.
- We start as before:
- [math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]
- [math]\displaystyle{ (E_{system_{f}} - E_{system_{i}}) + (E_{surroundings_{f}} - E_{surroundings_{i}}) = 0 }[/math]
- Note this time the system is just the child, and the significant surroundings (doing work) are the man and the Earth:
- [math]\displaystyle{ \Delta E_{child} - W + (E_{man_{f}} + E_{Earth_{f}}) - (E_{man_{i}} + E_{Earth_{I}}) }[/math]
- Plugging in more expressions gives:
- [math]\displaystyle{ (U_{child_{f}} + K_{child_{f}}) - (U_{child_{i}} + K_{child_{i}}) - W + (U_{man_{f}} + K_{man_{f}} + U_{Earth_{f}} + K_{Earth_{f}}) - (U_{man_{i}} + K_{man_{i}} + U_{Earth_{i}} + K_{Earth_{I}}) = 0 }[/math]
- Now we will isolate the final kinetic energy of the child, since this is proportional to the square of the final velocity:
- [math]\displaystyle{ K_{child_{f}} = W + (U_{child_{i}} - U_{child_{f}}) + K_{child_{i}} + (U_{man_{i}} - U_{man_{f}}) + (K_{man_{i}} - K_{man_{f}}) + (U_{Earth_{i}} - U_{Earth_{f}})+ (K_{Earth_{i}} - K_{Earth_{f}}) }[/math]
- We can simplify this by using the equation for gravitational potential energy and recognizing the terms the Earth adds are negligible. This gives:
- [math]\displaystyle{ K_{child_{f}} = W - \Delta U_{child} + K_{child_{i}} - \Delta U_{man} - \Delta K_{man} }[/math]
- The man is still at rest in this reference frame when the child reaches a distance [math]\displaystyle{ d }[/math], so his kinetic energy is 0. Furthermore, his position never changes relative to the Earth, so his change in gravitational potential energy is negligible:
- [math]\displaystyle{ K_{child_{f}} = W - \Delta U_{child} + K_{child_{i}} }[/math]
- Next, we know the child is at rest initially, so the initial kinetic energy of the child is 0. Also, the word done by the man will be the force times the distance:
- [math]\displaystyle{ K_{child_{f}} = Fd -\Delta U_{child} }[/math]
- We have found that the child's kinetic energy is equal to the negative of his/her change in gravitational potential energy plus the work done by the man, which makes sense. Plugging in expressions for each side of the equation gives:
- [math]\displaystyle{ \frac{1}{2}m{v_f}^2 = Fd - mgd = d(F - mg) }[/math]
- Finally, we get:
- [math]\displaystyle{ v_f = \sqrt{\frac{2d(F - mg)}{m}} }[/math]
Middling
Prove that the work done on an object in circular motion is always 0.
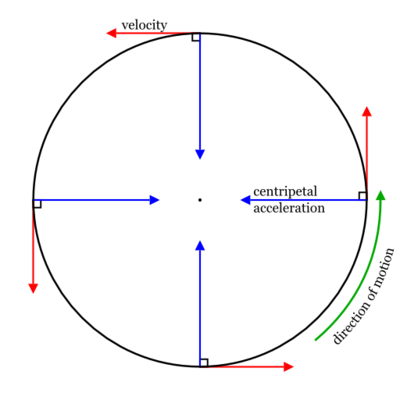
- To prove this, it will first be useful to define some variables and mention relevant equations:
- Variables:
- [math]\displaystyle{ m }[/math] will be the mass of the object
- [math]\displaystyle{ r }[/math] will be the radius of the circular motion
- [math]\displaystyle{ v }[/math] will be the speed of the object in circular motion
- [math]\displaystyle{ \mathbf{p} }[/math] will be the momentum of the object
- Expressions:
- [math]\displaystyle{ W = \Delta E = \int \mathbf{F} \bullet d\mathbf{r} \ \mathbf{(1)} }[/math] is the equation for the work done on an object. It says the work done on an object is the equal to the change in energy of the object, which is equal to the Force applied to the object dotted with the displacement vector of the object (A Line Integral)
- [math]\displaystyle{ F_c = \frac{mv^2}{r} \ \mathbf{(2)} }[/math] is the equation relating the needed centripetal force to the object's variables
- The next few equations come from the Curving Motion page. Referring to that page will be very helpful for this example.
- [math]\displaystyle{ \mathbf{F_{net}} = \mathbf{F_\parallel} + \mathbf{F_\perp} \ \mathbf{(3)} }[/math]
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} = \mathbf{F_\parallel} \ \mathbf{(4)} }[/math] (Change in magnitude of momentum)
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\perp = \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| = \mathbf{F_\perp} \ \mathbf{(5)} }[/math] (Change in direction of momentum)
- [math]\displaystyle{ \mathbf{F_{net}} = \frac{d\mathbf{p}}{dt} = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} + \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| \ \mathbf{(6)} }[/math]
- For an object to be in circular motion, its speed, which is tangential to the path, must not change. Otherwise, a spiraling inward or outward motion will occur. Therefore, it follows that the change in the magnitude of the momentum of the object must be [math]\displaystyle{ \mathbf{0} }[/math]. Using equation 4, were are led to:
- [math]\displaystyle{ \mathbf{F_\parallel} = \frac{d\mathbf{p}}{dt}_\parallel = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} = \mathbf{0} }[/math]
- This tells use that the parallel component of the net force on the object must also be [math]\displaystyle{ \mathbf{0} }[/math]:
- [math]\displaystyle{ \mathbf{F}_\parallel = \mathbf{0} }[/math]
- But if we circle back to the definition of work, using equations 1 and 3, we get:
- [math]\displaystyle{ W = \int \mathbf{F} \bullet d\mathbf{r} = \int \left (\mathbf{F}_\parallel + \mathbf{F}_\perp \right) \bullet d\mathbf{r} }[/math]
- Using the distributive property of dot products shows:
- [math]\displaystyle{ W = \int \left (\mathbf{F}_\parallel + \mathbf{F}_\perp \right) \bullet d\mathbf{r} = \int \mathbf{F}_\parallel \bullet d\mathbf{r} + \int \mathbf{F}_\perp \bullet d\mathbf{r} }[/math]
- We already showed that the parallel component of the net force must be [math]\displaystyle{ \mathbf{0} }[/math], so we come to:
- [math]\displaystyle{ W = \int \mathbf{F}_\perp \bullet d\mathbf{r} }[/math]
- Lastly, by the definition of the dot product, if the two vectors being dotted are always mutually perpendicular, then their dot product is always 0. The vector [math]\displaystyle{ \mathbf{r} }[/math] follows the curved path of the object, a circle, and points tangentially along the circle. Therefore, it is always tangent to the circle. The vector [math]\displaystyle{ \mathbf{F}_\perp }[/math] happens to always be perpendicular to the tangent of the circle by definition, since it is what is called the centripetal force. Therefore:
- [math]\displaystyle{ W = 0 }[/math]
- The statement "the work done on an object is 0" always holds for circular motion.
Difficult
The Earth orbits the Sun. The Moon orbits the Earth.
- a) With the Earth and the Moon as the system, and the Sun as the only surrounding doing work on the system, use the Energy Principle to create an expression for the change in the Kinetic Energy of the Earth:
- We start with the Energy Principle:
- [math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]
- We want to know an expression for the Kinetic Energy of the Earth. Since the Earth is part of the system, we first want to isolate the system:
- [math]\displaystyle{ \Delta E_{system} = - \Delta E_{surroundings} }[/math]
- Now, we will open up each term so that we may extract the Kinetic Energy term of the Earth:
- [math]\displaystyle{ \Delta U_{system} + \Delta K_{system} = -\Delta E_{surroundings} }[/math]
- [math]\displaystyle{ \Delta U_{system} + \Delta K_{Earth} + \Delta K_{Moon} = - \Delta E_{surroundings} }[/math]
- Rearranging gives:
- [math]\displaystyle{ \Delta K_{Earth} = - \left(\Delta E_{surroundings} +\Delta U_{system} + \Delta K_{Moon} \right) }[/math]
- b) With the Earth as the system, and the Moon and the Sun as the only surroundings doing work on the system, use the Energy Principle to create an expression for the Work done by the Sun on the Earth:
- From our Mathematical Model, we have:
- [math]\displaystyle{ E_{system_{f}} = E_{system_{i}} + W }[/math]
- The work term can be split into the Work done on the Earth by the Moon and the Work done on the Earth by the Sun:
- [math]\displaystyle{ W = W_{Moon} + W_{Sun} }[/math]
- Plugging this in gives us a way to solve for the Work done by the Sun on the Earth:
- [math]\displaystyle{ W_{Sun} = \Delta E_{system} - W_{Moon} }[/math]
- c) With the Sun as the system, and the Earth and the Moon as the only surroundings doing work on the system, use the Energy Principle to create an expression for the change in the Potential Energy of the Sun:
- We start with the Energy Principle:
- [math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]
- From this we deduce:
- [math]\displaystyle{ \Delta E_{system} = W }[/math]
- We will extract terms from this equation to find an expression of the Potential Energy of the Sun:
- [math]\displaystyle{ \Delta U_{system} + \Delta K_{system} = W_{Earth} + W_{Moon} }[/math]
- [math]\displaystyle{ \Delta U_{system} = (W_{Earth} + W_{Moon}) - \Delta K_{system} }[/math]
- Since the Sun is the system, we have:
- [math]\displaystyle{ \Delta U_{Sun} = (W_{Earth} + W_{Moon}) - \Delta K_{Sun} }[/math]
Connectedness
Industrial Engineering
- While this page refers mainly to thermodynamic and energy systems, I believe the concept of systems is essential to Industrial Engineers. Industrial Engineers work on making systems as efficient as possible by minimizing waste in the production process. They also merge people, machinery, information and energy to create a product or a service. People, machinery, information and energy can be considered a system. It is an industrial engineers job to figure out the most optimal way to merge parts of the system together in order to have the greatest impact or outflow from the system to the surroundings (consumers/customers). Industrial engineers work with open systems and strive towards having a net positive outflow (i.e the resources supplied produce greater output or value).
Chemical Engineering
- In addition, in regards to thermodynamic and energy systems, the concept of system & surroundings is important to Chemical Engineers. Chemical Engineers are required to accurately and efficiently identify the system they are working with in order to proceed with the necessary mass balance (and energy balance if applicable) calculations for the corresponding system. This system can be any sort of machinery, reacting plant, or even a bodily system.
History
The idea of a choice of system dates back to the 1800's. In this time many scientists and mathematicians were pushing the fronts of Classical Physics. In doing so, it was found from experiment and proved in theory that the Energy Principle was a fact. It followed that the choice of system and surroundings was ambiguous. Thus, it was useful to show that an infinite choice of systems is possible, but some are more useful than the others. Since then, this thought process has been passed down.
See also
Further reading
- Thinking about Physics Thinking by Professor Michael Schatz [1]
- Definition of Systems
- Isolated Systems Demonstration
- Bozeman Science
External links
- Curving Motion
- The Energy Principle
- Work/Energy
- Conservation of Energy
- Potential Energy
- Newton's Second Law: the Momentum Principle
- A Discussion of Air Resistance (Non-Conservative)
References
- MSU Open Source for Students
- Matter and Interactions 4th Edition