Fundamentals of Iterative Prediction with Varying Force
Claimed by Nick Gauthreaux, Fall 2020
It is rare to have a force which is perfectly constant, and iterative analysis of more realistic varying-force systems is substantially more complicated than analysis of constant force systems. A toy model demonstrates how programs may be written to analyze these systems.
Main Idea
The physics of iterative prediction with varying force is the same as for prediction with constant force, but it is necessary to generalize the mathematical expressions, which adds complexity to the code. This model will be an example of the Euler method, which is a first order iterative method. Because this is not the most efficient method of differential equations solving, it is also necessary to put thought into the computational details, such as the size of the time steps.
A Mathematical Model
To begin with, consider a one dimensional force, which may vary with both as a function of time and/or dependent variables such as position and velocity. Then we write this as [math]\displaystyle{ F(t,x,v) }[/math]. Now, using the momentum principle, we know that [math]\displaystyle{ F = \frac{\text{d}p}{\text{d}t} }[/math], which in discrete terms is [math]\displaystyle{ \Delta p = F\Delta t }[/math].
Just as with a constant force, this lets us write out for some iteration at [math]\displaystyle{ (t_0,x_0,v_0) }[/math] that
[math]\displaystyle{ p_{1} = p_{0} + F(t_0,x_0,v_0)\Delta t }[/math]
We wish to produce a full new set of variables [math]\displaystyle{ (t_1,x_1,v_1) }[/math], so we utilize the same methods as before:
[math]\displaystyle{ x_1 = x_0 + v_{avg}\Delta t = x_0 = \frac{p_1-p_0}{m}\Delta t }[/math]
[math]\displaystyle{ v_1 = \frac{p_1}{m} }[/math]
The difference we now have is that whereas before [math]\displaystyle{ F(t_0,x_0,v_0) = F(t_1,x_1,v_1) }[/math], we must now recalculate [math]\displaystyle{ F(t_1,x_1,v_1) }[/math] using the relevant formula. This will take the form of an extra step in each iteration. It is important to note that although we write the force as a function of all of these variables, in most cases it will only depend upon one of them. In a spring, for example, we will see that [math]\displaystyle{ F(t,x,v) = F(x) }[/math], meaning that only the position is necessary to compute the force.
A Computational Implementation
Code for an implementation of varying force iterative prediciton can be found in this Google colaboratory jupyter notebook. The following code snippet covers the physics calculation portions:
def calcmotion(self): #this is the method of the class which does the actual computation
#First, we want to know how many steps we will calculate, and round this to an integer
#Ideally, the user will make dur%tstep = 0, but we can't be sure, so we need to sanitize the input
numsteps = int(self.dur/self.tstep)
#Now we make an array to hold all of our data. For more information on numpy arrays, see
#https://docs.scipy.org/doc/numpy/user/basics.types.html
#It will have 5 columns and numsteps number of rows
#The columns are, in order, time, position, momentum, velocity, and force
#np.zeros takes a tuple for the shape of the array, and the optional argument dtype for the data type
#the plus 1 makes it so that we will end at the duration, instead of the duration - 1 timestep
self.data = np.zeros((numsteps+1,5),dtype=float)
#Now we perform the actual work of iterating:
for i in range(numsteps+1):
#Here we compute the time stamp of each step, but considering the iteration number and the timestep width
self.data[i,0] = i*self.tstep
#If this is the first step, we set our initial position and momentum
if i ==0:
self.data[i,1] = self.xinit
self.data[i,2] = self.pinit
#Otherwise, we use kinematics to compute a new position, and the momentum principle to compute a new momentum
else:
#pfinal = pinitial + F*delta t
self.data[i,2] = self.data[i-1,2] + self.data[i-1,4]*self.tstep
#We compute velocity using v = p/m
self.data[i,3] = self.data[i,2]/self.mass
#v_avg = (v_f + v_i)/2
vavg = (self.dat[i,3] + self.data[i-1,3])/2
#xfinal = xinitial + v_avg*delta t
self.data[i,1] = self.data[i-1,1] + vavg*self.tstep
#Finally, we compute the force at our new position
self.data[i,4] = self.forcefunc(self.data[i,0],self.data[i,1],self.data[i,2])
return self.data
First, time data is computed by simply iterating over each time step, since we are using even steps. Next, if this is the first iteration, initial position and momentum data is input. If it is not the first iteration, then the momentum and position of the previous step are read to determine the new position, and the force and momentum of the previous step are read to determine the new force. Finally, the velocity column is filled out using the definition of momentum, and the new force is computed using the user defined force function.
The rest of the notebook consists of the code used to define these functions, and to view the results, both as plots and as animations.
Examples
Simple
Imagine a force on an object is defined by
[math]\displaystyle{ F=kx }[/math]
Where [math]\displaystyle{ k = 3 N/m }[/math]. Now, assume the object has an initial position of [math]\displaystyle{ x_0 = 5 m }[/math], and an initial momentum of [math]\displaystyle{ p = 0 }[/math]. After a time step of [math]\displaystyle{ 0.2 s }[/math], what will be the object's new momentum according to our model?
We have the formula [math]\displaystyle{ \Delta p = F \Delta t }[/math]. We may compute [math]\displaystyle{ F = (3 N/m)(5m) = 15 N }[/math], so plugging this in gives [math]\displaystyle{ \Delta p = (15 N)(0.2 s) = 3 N\cdot s = 3 \frac{kg\cdot m}{s} }[/math]
Moderately Difficult
Now, using the a varying force iterative motion script - either the one given above or your own - let's compute a motion prediction. Take the force defined above, with [math]\displaystyle{ k = 3 N/m }[/math] as above. Choose the initial position this time to be [math]\displaystyle{ 0.1 m }[/math], and let the initial momentum still be zero. Taking time steps of [math]\displaystyle{ 0.2 s }[/math] as above, what will be its position after 5 seconds? Include a plot of position versus time. What standard function does this plot resemble?
Plugging the problem into the above program produces a final position of [math]\displaystyle{ 163.6 m }[/math] (if this seems a bit small to you, make sure to do the difficult portion of the problem), and a plot that looks like this:
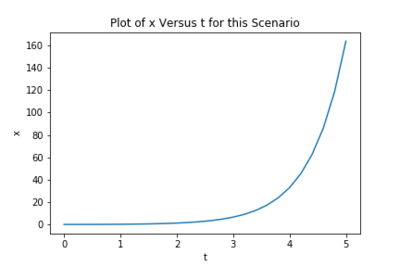
This plot should be recognizable as an exponential function. In fact any force defined with the generic formula [math]\displaystyle{ F = kx }[/math] will produce an exponential position curve, so long as [math]\displaystyle{ k \gt 0 }[/math]. As it happens, the case [math]\displaystyle{ k \lt 0 }[/math] happens much more frequently in nature, and will be dealt with in the page Simple Harmonic Motion.
Difficult
Using the same situation as above, let's now turn down the time step to [math]\displaystyle{ 0.01 s }[/math]. What is the final position now? Keep decreasing the time step until this converges to a final value. What is this value? If you can, try writing this in terms of fundamental constants and the parameters of the problem (hint: think about the discussion of the what the function looks like given above). If you haven't had any experience with differential equation this will be difficult, but the answer is very instructive. Think about why changing the time step caused such a radical difference, and give a brief explanation of your thoughts.
At a time step of [math]\displaystyle{ 0.01 s }[/math], the answer will come out to be [math]\displaystyle{ 279.11 m }[/math], which is dramatically larger than the result above. However, as we continue reducing the time step, we see that it converges to a value of [math]\displaystyle{ 288.45 m }[/math]. This may be expressed exactly as [math]\displaystyle{ 0.05 e^{\sqrt{3}t} }[/math]. To arrive at this value requires an understanding of differential equations, so if this is not familiar to you don't worry. One straightforward way of arriving at the solution is to use a language such as Mathematica/WolframAlpha. The below gives Mathematica code (if you are a Georgia Tech student, you have a freely available Mathematica license, and it can be a very useful program), in which one is able to specify the initial condition:
DSolve[{x"[t] == 3*x[t], x[0] == 0.1, x'[0] == 0}, x, t]
This is the simplified version required to make WolframAlpha run:
DSolve[x"[t] == 3*x[t], x,t]
This version will leave constants which you must solve. For a description of how this is done, see the solution below. Either way, you may notice that the result that these give (with constants filled in) is actually [math]\displaystyle{ 0.05 e^{-\sqrt{3} t} (1 + e^{2 \sqrt{3} t}) }[/math]. However, we can multiply this through, and arrive at the value above, plus [math]\displaystyle{ 0.05 e^{-\sqrt{3}t} }[/math]. This value is essentially 0, so we can ignore it. Now, how do we go about getting to the answer Mathematica gives us? We will solve this by ansatz (a.k.a. guessing) that the exponential function will form the base of our solution, with some constants involved. However, we can't know whether it is an exponential with a positive exponent or with a negative exponent, so we assume it is a sum of each, with each having different constants. Newton's second law gives an equation of motion
[math]\displaystyle{ x''(t) = \frac{k}{m} x }[/math]
We also have initial conditions [math]\displaystyle{ x(0) = 0.1 }[/math] and [math]\displaystyle{ x'(t) = 0 }[/math]. Then plugging in our guess [math]\displaystyle{ x(t) = A e^{Ct} + Be^{-Ct} }[/math] gives us that
[math]\displaystyle{ x''(t) = AC^2e^{Ct} + BC^2e^{-Ct} = C^2 x(t) = \frac{k}{m} x(t) }[/math]
Then we have that [math]\displaystyle{ C^2 = k/m = 3 N/m }[/math]. Next, we need to determine constants A and B. First, we have that
[math]\displaystyle{ x(0) = A + B = 0.1 }[/math]
Next, using the second initial condition, we differentiate and find that
[math]\displaystyle{ x'(0) = 0 = AC - BC }[/math]
Combined, these gives us that [math]\displaystyle{ A = B = 0.05 }[/math]. Plugging all this in gives us the answer that Mathematica gave. Now, why did having a wide time step lead us to be so far off? In a constant force case, the amount of error is linear when we perform these computations. When the force is varying, however, the error builds up over time. For a system which changes as quickly as the exponential case we considered, it builds up very quickly, and puts us very far off, unless we use an adequately small time step.
Connectedness
Applications in Chemical Engineering include models of processes that include forces on chambers in reaction batch processes. An example of this would be in processes that involve regulation of volume, particularly through container volume. Forces in such a model would likely vary with respect to pressure, and would change over time according to the initial state of substances in the container. An automated process like this would likely include some sort of code similar to that pictured above, where the force required to keep volume constant is proportional to some way to the change in pressure exerted by the process approaching equilibrium.
For example, in a process serving to saturate water with some gaseous substance, keeping volume constant using a model like the one above to dictate a force exerted on the container serves to artificially shift pressure equilibrium by increasing container pressure. When satisfactory conditions have been met, the products of the process, a supersaturated liquid, are extracted and used further on. A process like this would require a varying force model in order to make adjustments as pressure continually changed in the container.
History
The type of numerical solution method we are using is called Euler's Forward Method[1], and was developed by its namesake (when one is in science and math, one will find a great many things named after Leonhard Euler [2]). Numerical methods such as this are used frequently to solve physical systems described by differential equations for which no solution exists, and so appear in all facets of science, mathematics, and engineering. In the movie Hidden Figures, Euler's Method is used as a plot device, and although this is not strictly accurate, numerical methods were - and are - used extensively in orbital calculations [3]. Most modern computation uses the Runge-Kutta method [4] or other more advanced methods, which converge with much wider time steps, and so are much more computationally efficient.
See also
- Kinematics
- Iterative Prediction
- Newton's Second Law: the Momentum Principle
- Vectors
- SI Units
- Velocity
- Acceleration
- Iterative Prediction
- Simple Harmonic Motion
- Iterative Prediction of Spring-Mass System
- Newton's Second Law: the Momentum Principle
- Kinematics
- Predicting Change in multiple dimensions
- Two Dimensional Harmonic Motion
Further Reading
- Matter and Interactions, 4th Edition