Acceleration

From Physics Book
Jump to navigation Jump to search

CLAIMED BY ETHAN STONE (FALL 2021) This page defines and describes acceleration.

The Main Idea

Acceleration, denoted by the symbol [math]\displaystyle{ \vec{a} }[/math], is a vector quantity defined as the rate of change of Velocity with respect to time. In calculus terms, it is the time derivative of the velocity vector. Acceleration indicates a change in the velocity vector's magnitude, direction, or both. Acceleration is an instantaneous value, so it may change over time. In physics, the acceleration of particles is caused by forces. The most commonly used metric unit for acceleration is the meter per second per second (m/s/s or m/s2).

A Mathematical Model

This graphic was found here on the Wikimedia commons, where it was uploaded by user 'Fred the Oyster.' It is provided on the commons under an Attribution-ShareAlike 4.0 International license. It is shown here under the same license.

Instantaneous acceleration [math]\displaystyle{ \vec{a} }[/math] is defined as:

[math]\displaystyle{ \vec{a} = \frac{d\vec{v}}{d t} }[/math]

where [math]\displaystyle{ \vec{v} }[/math] is a velocity vector and [math]\displaystyle{ t }[/math] is time.

Effect on Velocity Vector

Acceleration indicates a change in the velocity vector's magnitude, direction, or both:

  1. Any component of the acceleration vector parallel to the velocity vector indicates an increase in velocity magnitude/ speed.
  2. Any component of the acceleration vector anti-parallel to the velocity vector indicates a decrease in velocity magnitude/ speed.
  3. Any component of the acceleration vector perpendicular to the velocity vector indicates a change in the velocity vector's direction.

Average Acceleration

Since acceleration is an instantaneous quantity, it can change over time. Over any given time interval, there is an average acceleration value denoted [math]\displaystyle{ \vec{a}_{avg} }[/math]. The average acceleration over an interval of time [math]\displaystyle{ \Delta t }[/math] is given by

[math]\displaystyle{ \vec{a}_{avg} = \frac{\Delta \vec{v}}{\Delta t} }[/math].

As the duration of the time interval [math]\displaystyle{ \Delta t }[/math] becomes very small, the value of the average acceleration over that time interval approaches the value of the instantaneous acceleration at any point in time within that interval.

Derivative Relationships

Acceleration is the time derivative of velocity, which is in turn the time derivative of position, so acceleration is the second time derivative of position.

Recall that

[math]\displaystyle{ \vec{a}(t) = \frac{d\vec{v}(t)}{dt} }[/math]

and

[math]\displaystyle{ \vec{v}(t) = \frac{d\vec{r}(t)}{dt} }[/math].

Therefore:

[math]\displaystyle{ \vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2} }[/math].

Integral Relationships

The time integral of acceleration yields velocity, and the time integral of velocity yields position, so the double time integral of acceleration yields position.

[math]\displaystyle{ \vec{v}(t) = \int \vec{a}(t) \ dt }[/math]

and

[math]\displaystyle{ \vec{r}(t) = \int \vec{v}(t) \ dt }[/math].

Therefore

[math]\displaystyle{ \vec{r}(t) = \iint \vec{a}(t) \ dt \ dt }[/math].

Kinematic Equations

The kinematic equations can be derived from the derivative and integral relationships between acceleration, velocity, and displacement. For the equations and more information, view the Kinematics page.

Newton's Second Law of Motion

In physics, the acceleration of particles is caused by forces. Newton's Second Law: the Momentum Principle states that

[math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math].

From this relation, it can be derived that

[math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math]

, or that

[math]\displaystyle{ \vec{a} = \frac{\vec{F}_{net}}{m} }[/math].

This makes sense because acceleration should be directly proportional to force, which causes it, and inversely proportional to mass, which resists it (see Inertia). This equation is often used to find the acceleration of a particle. If that acceleration is constant, kinematic equations are then often used to determine how its position and velocity change over time.

A 1-Dimensional Graphical Model

Below are some graphs relating velocity and position along one dimension to time as a result of varying types of acceleration. Because of the derivative and integral relationships between position, velocity, and acceleration:

  1. The slope of a position-vs-time graph at any point in time is the velocity of the particle at that point in time.
  2. The slope of a velocity-vs-time graph at any point in time is the acceleration of the particle at that point in time.
  3. The area under a velocity-vs-time graph over a time interval is the change in the position of the particle over that time period.
  4. The area under an acceleration-vs-time graph over a time interval is the change in the velocity of the particle over that time period.

Constant Acceleration

When the acceleration of a particle is constant over time, its velocity is changing at a constant rate, and therefore is graphed as a straight line. The acceleration is the slope of the velocity graph; a positive acceleration means the velocity is increasing and should have a positive slope, and a negative acceleration means the velocity is decreasing and has a negative slope.

If the velocity of a particle is constant over time, the slope of the graph and the acceleration of the particle are 0.

Note that in both of the above graphs, the y-intercept was at a velocity of 0. This is because it was assumed that the particles began at rest. If a particle has other initial conditions, the graph must reflect them. For example, below is the graph of the velocity of a vertically thrown ball over time (see Projectile Motion).

Its initial velocity is positive because the ball is thrown upwards, which we define as the positive direction. However, as time goes on, its velocity decreases at a steady rate due to the constant acceleration of gravity, until it reaches 0. At this point, the ball has reached the highest point in its trajectory; it is moving neither upwards nor downwards. Gravity continues to accelerate the ball downwards, so its velocity becomes negative and the ball moves back towards earth. If the ball lands at the same height as that from which it was thrown, the positive area under the left side of the graph equals the negative area under the right side of the graph because the distance traveled upwards during the first half of the flight equals the distance traveled downwards in the second half of the flight. The total area under the graph would be 0 because the final position is the same as the initial position. The slope of the velocity graph is -g at all points of this graph.

In addition to velocity, it can be useful to visualize the position of a particle over time when it undergoes constant acceleration. The graph below shoes the position of a particle over time when it begins at rest at the origin and undergoes constant positive acceleration.

At first, the position of the particle is barely changing over time, because in the beginning of the particle's motion, its velocity is still small. However, as the velocity steadily increases as a result of the constant positive acceleration, the slope of the position graph increases, showing that towards the end of its motion, the particle is moving greater distances in shorter time intervals. The slope of the position graph, which is the velocity of the particle, is increasing at a steady rate, resulting in a parabolic position graph. The kinematic equation corresponding to this graph is [math]\displaystyle{ r_f = \frac{1}{2} a * t^2 + v_i * t + r_i }[/math].

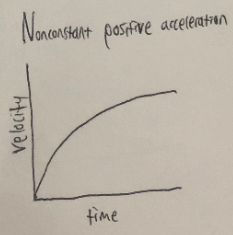
Nonconstant Acceleration

When acceleration is not constant, the velocity-vs-time graph is not a straight line but a curve. The nature of the curve depends on how the acceleration changes. An everyday example of an object that accelerates non-uniformly is a car. Cars typically undergo positive but decreasing acceleration when they begin moving from rest. This is what a car's velocity-vs-time graph might look like:

At first, the car has a high acceleration, and its velocity changes rapidly. However, as it approaches its target speed, its acceleration decreases.

A Computational Model

In the simulation below, a particle initially moving to the right undergoes a leftward acceleration followed by an upward acceleration. The purple arrow represents the particle's velocity and the red arrow represents its acceleration. Notice that the tip of the purple arrow always moves in the direction indicated by the red arrow.

Click here for acceleration simulation

Iterative Prediction is used to update the position of the particle. Click "view this program" in the top left corner to view the source code.


Circular Motion

Acceleration is also an important part of circular motion. Circular motion In circular motion there are two types of acceleration: centripetal and tangential.

Centripetal Acceleration

Centripetal Acceleration does not have an actual effect on the magnitude of the velocity vector of an object traveling in circular motion. Due to the fact that the direction of the velocity vector is constantly changing while revolving around a point, there is an acceleration present. This acceleration is called centripetal acceleration.

We can determine the centripetal acceleration given a speed [math]\displaystyle{ v }[/math], and radius [math]\displaystyle{ r }[/math] using the equation

[math]\displaystyle{ a_c = \frac{v^2}{r} }[/math]

The direction of centripetal acceleration is always directed toward the center of the circle, orthogonal to the velocity vector. If the magnitude of the velocity vector stays constant, the particle is considered moving in uniform circular motion.

If given angular velocity ω, we can use the equation

[math]\displaystyle{ ω = \frac{v}{r} }[/math]

to derive that centripetal acceleration can be found with the equation

[math]\displaystyle{ a_c = -ω^2r }[/math].

Tangential Acceleration

If a particle is speeding up or slowing down, the particle is moving in non-uniform circular motion and has a tangential acceleration. To find the magnitude of tangential acceleration we first need to find angular acceleration. Given change in angular velocity Δω, and change in time Δt, angular acceleration α, can be found using the formula

[math]\displaystyle{ α = \frac{Δω}{Δt} }[/math]

Using our angular acceleration α, and radius r, we can then find tangential acceleration [math]\displaystyle{ a_t }[/math], using the formula

[math]\displaystyle{ a_t = rα }[/math]

The direction of tangential acceleration follows the direction of tangential velocity and is orthogonal to the radius of the circle.


Net Acceleration

To find the magnitude of the net acceleration [math]\displaystyle{ a_n }[/math] of a particle moving in circular motion you need to first calculate both the centripetal acceleration [math]\displaystyle{ a_c }[/math] and the tangential acceleration [math]\displaystyle{ a_t }[/math]. You would then use the equation

[math]\displaystyle{ a_n = \sqrt{a_c^2 + a_t^2} }[/math]


Examples

Some of these example problems make use of the kinematic equations. For more practice using those, try the practice problems on the Kinematics page.

1. (Simple)

Question:

A motorcycle accelerates uniformly from rest to a speed of 7.10 m/s over a distance of 35.4 m. Determine the acceleration of the motorcycle.


Solution:


Given:

[math]\displaystyle{ v_i = 0 m/s }[/math]
[math]\displaystyle{ v_f = 7.10 m/s }[/math]
[math]\displaystyle{ d = 35.4 m }[/math]

Find:

[math]\displaystyle{ a = ? }[/math]

Calculations:

[math]\displaystyle{ v_f^2 = v_i^2 + 2ad }[/math]
[math]\displaystyle{ 2ad = v_f^2 - v_i^2 }[/math]
[math]\displaystyle{ a = \frac{v_f^2 - v_i^2}{2*d} }[/math]
[math]\displaystyle{ a = \frac{(7.10m/s)^2 - (0m/s)^2}{2*35.4m} }[/math]
[math]\displaystyle{ a = 0.712 m/s^2 }[/math]

2. (Simple)

Question:

A rabbit can jump to a height of 2.62 m. Determine the takeoff speed of the rabbit.


Solution:

Given:

[math]\displaystyle{ a = -9.8 m/s^2 }[/math]
[math]\displaystyle{ v_f = 0 m/s }[/math] *Considering the moment of takeoff to maximum height
[math]\displaystyle{ d = 2.62 m }[/math]

Find:

[math]\displaystyle{ v_i = ? }[/math]

Calculations:

[math]\displaystyle{ v_f^2 = v_i^2 + 2ad }[/math]
[math]\displaystyle{ v_i^2 = 2ad - v_f^2 }[/math]
[math]\displaystyle{ v_i = \sqrt{2ad - v_f^2} }[/math]
[math]\displaystyle{ v_i = \sqrt{2*-9.8m/s^2*2.62m - (0m/s)^2} }[/math]
[math]\displaystyle{ v_i = 7.17 m/s }[/math]

3. (Simple)

Question:

A rock is dropped from a bridge into a lake and is heard to hit the water 3.41 s after being dropped. Determine the height of the bridge above the water.


Solution:

Given:

[math]\displaystyle{ a = -9.8 m/s^2 }[/math]
[math]\displaystyle{ t = 3.41 s }[/math]
[math]\displaystyle{ v_i = 0 m/s }[/math]

Find:

[math]\displaystyle{ d = ? }[/math]

Calculations:

[math]\displaystyle{ d = v_i*t + 0.5*a*t^2 }[/math]
[math]\displaystyle{ d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s^2)*(3.41 s)^2 }[/math]
[math]\displaystyle{ d = 0 m + 0.5*(-9.8 m/s^2)*(11.63 s^2) }[/math]
[math]\displaystyle{ d = -57.0 m }[/math] (57.0 meters deep)

4. (Simple)

Question:

The initial velocity of a particle is <-4, 3, -12>m/s. After 4 seconds, the velocity of the particle is <-8, 3, 8>m/s. What was the particle's average acceleration during the 4 second interval?


Solution:

[math]\displaystyle{ \vec{a}_{avg} = \frac{\Delta \vec{v}}{\Delta t} = \frac{\vec{v}_f - \vec{v}_i}{\Delta t} = \frac{\lt -8, 3, 8\gt - \lt -4, 3, -12\gt }{4} = \frac{\lt -4, 0, 20\gt }{4} = \lt -1, 0, 5\gt }[/math]m/s

Note that at any given moment, the acceleration of the particle may be something other than <-1, 0, 5>; this is simply the average acceleration over the 4s interval. (However, according to the mean value theorem, there must be some point in time within the interval at which the acceleration of the particle is the average acceleration.)

5. (Middling)

Question:

A particle is travelling at a speed of 5m/s. The particle undergoes a nonconstant acceleration in the direction of its velocity for 1 second. The magnitude of the acceleration is given by [math]\displaystyle{ a = 6 - 6t^2 }[/math], where t=0 is the beginning of the 1 second interval. What is the final speed of the particle?


Solution:

[math]\displaystyle{ v_f = v_i + \int_{t_i}^{t_f} a(t) \ dt }[/math]
[math]\displaystyle{ v_f = 5 + \int_0^1 6 - 6t^2 \ dt }[/math]
[math]\displaystyle{ v_f = 5 + [6t - 2t^3]_0^1 }[/math]
[math]\displaystyle{ v_f = 5 + 4 = 9 }[/math]m/s

6. (Middling)

Question:

The velocity of a particle as a function of time is given by the expression [math]\displaystyle{ \vec{v}(t) = \lt 6t, 10 \sin t, 4\gt }[/math]. What is the acceleration of the particle as a function of time?


Solution:

[math]\displaystyle{ \vec{a}(t) = \frac{d \vec{v}(t)}{dt} }[/math]
[math]\displaystyle{ \vec{a}(t) = \frac{d}{dt} \lt 6t, 10 \sin t, 4\gt }[/math]
[math]\displaystyle{ \vec{a}(t) = \lt 6, 10 \cos t, 0\gt }[/math]

Connectedness

Acceleration has applications in all parts of the physical universe. It is necessary for all changes in motion.

Application: rocket launch

When a rocket is launched, its thrusters cause it to accelerate upwards. The desired acceleration must be calculated to within a certain range; too small an acceleration would result in the rocket being unable to achieve an escape velocity, while too large an acceleration would result in too much stress on the rocket structure or on the passengers. When the desired acceleration has been found, Newton's second law must be used in conjunction with the rocket's mass to determine what force the thrusters should exert on the rocket.

See also

External links

References

  • Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. 4th ed. Hoboken, NJ: John Wiley & Sons, 2015. Print.
Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Acceleration&oldid=39305"