Work/Energy
𝐌𝐀𝐑𝐂 𝐁𝐎𝐘𝐄𝐑 𝐒𝐏𝐑𝐈𝐍𝐆 𝟐𝟎𝟐𝟑
The Main Idea
Up until this point, we have worked with applying the Energy Principal in situations where there is no work. Therefore, assuming there is no heat lost to surroundings, the energy equation would reduce to ΔE = 0 or Esystem = Esurroundings. But what if there is work being done on or by the system? It is important to note that the definition of work is the transfer of energy between the system and the surroundings due to some force. Also only the component of the force that is parallel to the displacement of the system contributes to the work done by the surroundings. In this section we will cover what work is and how we will use it.
Work measures the transfer of energy to an object due to a force applied along its displacement. A person pushing a box, jogging to work, or pulling a wagon are all examples of doing work. This page will first explore the definition of work, then proceed to explain the relationship between work and energy, specifically the Work-Energy Theorem, which states that the net work that acts on a particle is equivalent to the change in kinetic energy of the particle.
Isolated System
An isolated system is one in which there is no work done on the system by the surroundings or vice versa. In this case W = 0.
A Mathematical Model of Work
There are two definitions of work: one where work is constant and one where it is not. When force is constant, it can be defined as W = [math]\displaystyle{ \vec F }[/math] ∙ [math]\displaystyle{ \cos(θ) }[/math] ∙ [math]\displaystyle{ \vec x }[/math], where θ is the angle between the force vector and the displacement vector - remember, only the component of the force that actually results in displacement contributes to work. When the force is not constant, the best definition of work is as an integral, expressed as: [math]\displaystyle{ \int_{x_1}^{x_2} \vec {F}\\cos(θ) \vec {dx}\ }[/math]. This is the integral of the force evaluated over bounds from initial to final position, x1 and x2, respectively.
Dot Products
A dot product is a mathematical operator that serves to multiply two vectors. It is crucial to the idea of work, because under a constant force, Work can be expressed as W = [math]\displaystyle{ \vec F }[/math] ∙ [math]\displaystyle{ \cos(θ) }[/math] ∙ [math]\displaystyle{ \vec x }[/math].
Algebraic Computation
To compute the dot product of two vectors, multiply chronological corresponding elements in the vector together and add them all up.
For instance, the dot product <3,2,1> ∙ <5,6,7> could be written as (3*5)+(6*2)+(7*1) and would equal 15+12+7 = 34
Take note that taking the dot product of two vectors yields a scalar
Geometric Explanation
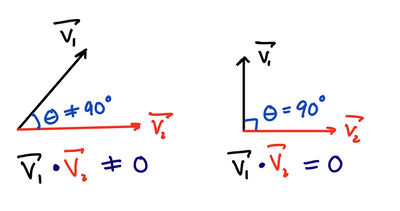
Taking the dot product of two vectors can give you a feel for the positions of those two vectors in space. For example, the dot product of two perpendicular vectors is zero.
Practice Problems
Compute the following dot products
1) <34,2,7>∙<2,1,0>
2) <0,0,0>∙<930843029,43982048,43291>
3) <1,1,1,0,7,3,2>∙<2,4,2,5,7,8,0>
Answers:
1)70
2) 0
3)81
Explanation of Steps:
1)(34 * 2) + (2 * 1) + (7 * 0) = 70
2) Since one vector is the zero vector, each component of the other vector will just be multiplied by 0, yielding an overall dot product of 0
3)(1 * 2) + (1 * 4) + (1 * 2) + (0 * 5) + (7 * 7) + (3 * 8) + (2 * 0) = 81
As stated earlier, under a constant force, work can be expressed as W = [math]\displaystyle{ \vec F }[/math] ∙[math]\displaystyle{ \cos(θ) }[/math] ∙ [math]\displaystyle{ \vec x }[/math]. This will often be the formula used in this course. Keep in mind that this is a dot product, so if these two vectors are perpendicular to one another, the dot product (and therefore the work) will equal zero. This is because if two vectors are perpendicular to each other, the angle between them is 90°, and cos(90°) is always zero. Conceptually, this makes sense because if the force vector is perpendicular to the displacement vector, there is no component of the force vector in the direction of the displacement, meaning it does neither positive nor negative work. This is a key connection to be made about work.
Work and Energy Theorem (Mathematical Model)
The Work-Energy Theorem states that the net work that acts on a particle is equivalent to the change in kinetic energy of the particle. Recall Newton's second law: [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math]. Also remember that [math]\displaystyle{ \vec{v} }[/math] is equivalent to [math]\displaystyle{ \frac{d\vec{x}}{dt} }[/math], the change in position over the change in time. This can also be rearranged to: [math]\displaystyle{ \vec{dx} = \vec{v} }[/math] ∙ [math]\displaystyle{ \vec{dt} }[/math]. We can therefore substitute [math]\displaystyle{ \vec{dx} }[/math] in the work integral formula with [math]\displaystyle{ \vec{v} }[/math] ∙ [math]\displaystyle{ \vec{dt} }[/math] and integrate over time instead, which would look like this: [math]\displaystyle{ \int_{t_1}^{t_2} \vec {F} \vec{v} }[/math] ∙ [math]\displaystyle{ \vec{dt}\ }[/math]
However, now remember that [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] and that [math]\displaystyle{ \vec{a} }[/math] is equivalent to [math]\displaystyle{ \frac{d\vec{v}}{dt} }[/math], the change in velocity over change in time. Thus, we can take a second step and replace the [math]\displaystyle{ \vec{F} }[/math] force vector in the work integral with [math]\displaystyle{ \ m\frac{d\vec{v}}{dt} }[/math], yielding a final work integral of:
[math]\displaystyle{ \int_{t_1}^{t_2} m\frac{d\vec{v}}{dt} \vec{v} }[/math] ∙ [math]\displaystyle{ \vec{dt}\ }[/math] or [math]\displaystyle{ \int_{t_1}^{t_2} m\vec{v}\vec{dv}\ }[/math].
Now, when you perform the integration, you will have:
[math]\displaystyle{ \int_{t_1}^{t_2} m\vec{v}\vec{dv}\ }[/math] = [math]\displaystyle{ {\frac {1}{2}}mv_{t2}^{2} - {\frac {1}{2}}mv_{t1}^{2} }[/math].
Recalling that kinetic energy, KE, is equal to [math]\displaystyle{ {\frac {1}{2}}mv^{2} }[/math], this new expression for work is equal to the final kinetic energy minus the initial, or in other words, the change in kinetic energy. We have therefore proved that the net work done on a system is equal to the change in kinetic energy of the system, which we can represent with this formula:
[math]\displaystyle{ W_{net} }[/math] = [math]\displaystyle{ ΔKE }[/math] = [math]\displaystyle{ {\frac {1}{2}}mv_{t2}^{2} - {\frac {1}{2}}mv_{t1}^{2} }[/math].
A Computational Model
Below is a link to a Glowscript computational model showing how the net work done on an object is equivalent to its change in kinetic energy. In this model, an object is slowing down in velocity due to a force acting against its displacement, so both the work and the change in kinetic energy are zero:
https://www.glowscript.org/#/user/mbonyx20/folder/WorkEnergyTheorem/
You can play around with the velocity, force, etc in this code.
Examples
Easy
A jogger goes for a 3 mile jog around a lake averaging 3m/s. She starts and finishes at her home. How much work does she do?
Solution: The formula for work is (FORMULA). In this problem, the Δx is zero, because the jogger ends up at the same place she started. Therefore, the total work is zero.
Medium
A 5kg box is dragged 2m across the floor with a rope pulling with a force of 10N at a 30 degree angle. How much work is done?
Solution:
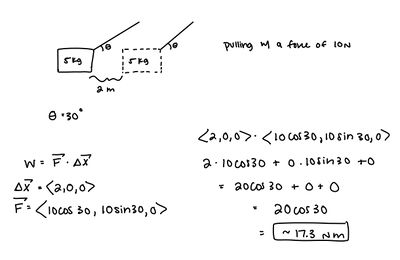
Medium
Hard
Hard
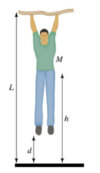
You hang by your hands from a tree limb that is a height L above the ground, with your center of mass a height h above the ground and your feet a height d above the grown, as shown in the figure (not to scale). You then let yourself fall. You absorb the shock by bending your needs, ending up momentarily at rest in a crouched position with your center of mass a height b above the ground. Your mass is M. You will need to draw labeled physics diagrams for the various stages in the process.
Connectedness
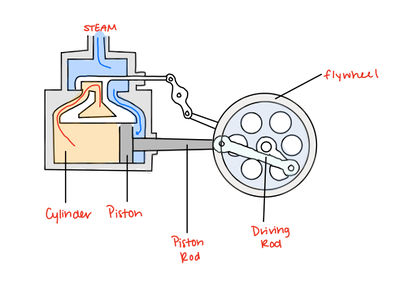
As discussed in the "history" section of this page, the term "work" has close ties to the invention of the steam engine. A steam engine works in two major steps.
(1) A fire heats up water to make steam
(2) the steam causes a piston to move up and down, powering some sort of engine.
This simple and effective invention was used widely in the seventeen and eighteen hundreds to transport ships across waterways and make factories have functioning machinery. The concept of turning thermal energy, which can be difficult to harness into mechanical energy, which is easy to use, revolutionized transportation and automation - and it all relies upon the concept of work!
History

see citation 1
The concept of work is so fundamental to our modern understanding of physics that it is difficult to trace back its exact origins. It is thought, though that french mathematician Gaspard-Gustave Coriolis was the first to coin the term. At the time, he didn't understand the wide reaching applications of the term but used it nonetheless in a paper he published in 1835 to describe a force acting over a distance. He did not intend it to be used in a wide variety of disciplines in science (particularly in physics), but rather for it to be a term describing the motion of steam engines in producing energy.
The scientist who made "work" into the term it is today is Solomon of Caux. He too worked closely with steam engines but broadened and popularized the term work into what more closely resembles how we use it today.
Since that time, its mathematical and conceptual definition has become more complete and is pops up in many different disciplines from Classical Physics to Thermodynamics.
More Info
(1) https://www.britannica.com/biography/Gustave-Gaspard-Coriolis
(2) https://www.lindahall.org/gustave-coriolis/