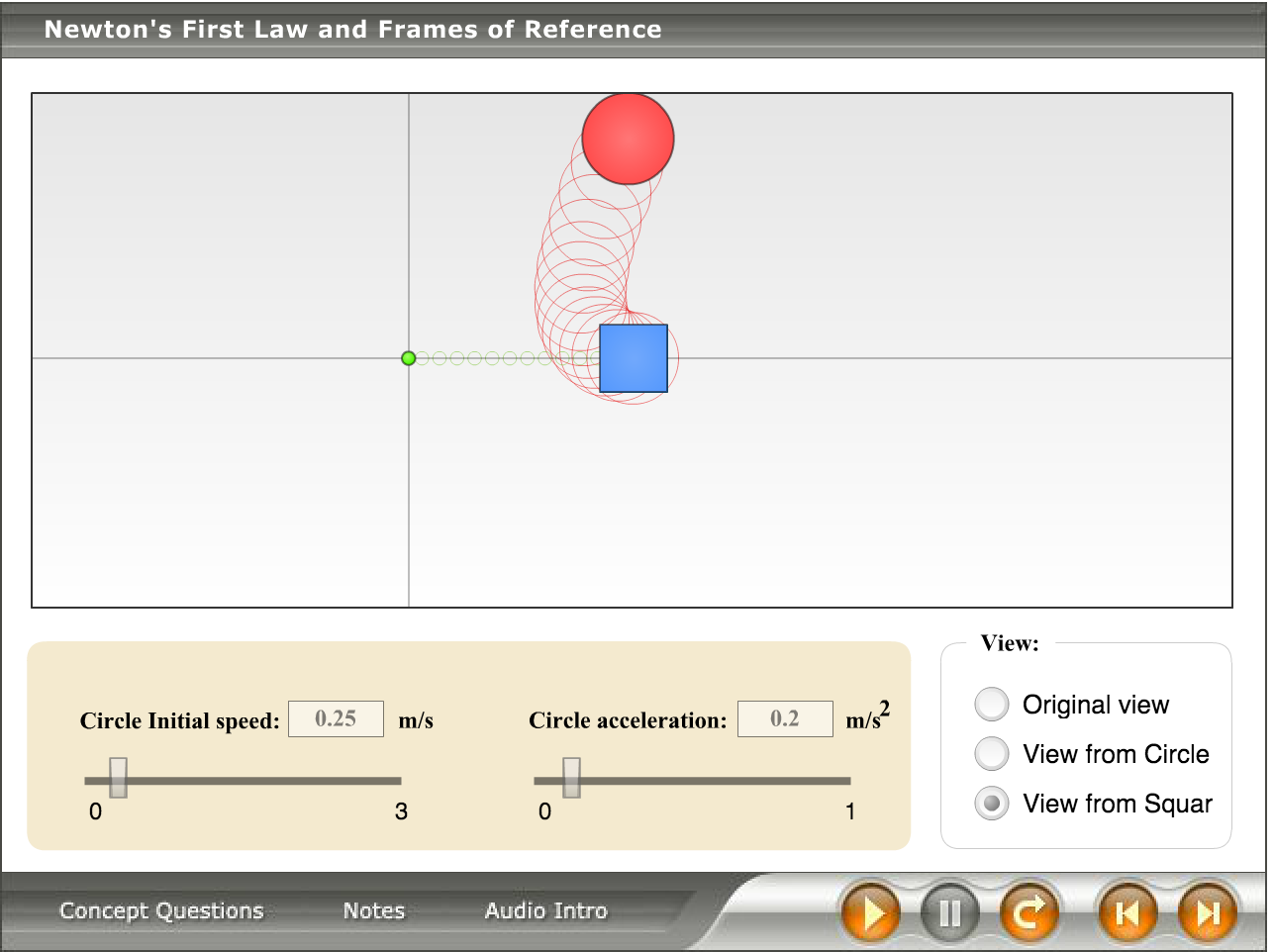
Frame of Reference
Created by Abdulaziz Alabbady Summer 2022

The frame of reference is a tool that can be used to change the way in which a system is viewed, thus adding a layer of complexity but in some cases simplifying the problem.
The Main Idea
A frame of reference is the point in the way or perspective from which you view the events that take place within a system. In this class we use inertial frames of reference, or frames of reference moving at constant velocities. (See the "inertial reference frames" section on the Inertia page for more information.) It is easy to think about if you imagine a person and what they would see if they were standing where you want a frame of reference to be. Consider the below example where there are two frames of reference: The one that observes the whole train and the boy and the one from the point of view of the boy on the train.

To the first observer (and his frame of reference), the boy is moving to the right along with the train. To the boy on the train (and his different frame of reference), he is standing still on the train. Here is a basic example of how changing the frame of reference can be a very powerful tool.
A Mathematical Model
In order to calculate what the velocity is, we will use the following equation so that the frame of reference will not change the overall value of the velocity:
[math]\displaystyle{ \vec{v} = \vec{v}' + \vec{v}_{frame} }[/math]
where [math]\displaystyle{ \vec{v} }[/math] is the velocity in a stationary frame, [math]\displaystyle{ \vec{v}_{frame} }[/math] is the velocity of the moving reference frame, and [math]\displaystyle{ \vec{v}' }[/math] is the velocity observed in the moving frame.
A Computational Model
There are some great resources that can help you become more acquainted with the topic of frames of reference.
The following website allows you to change initial conditions and frames of reference to see exactly how your decisions will change what is seen: http://www.wiley.com/college/halliday/0470469080/simulations/sim45/sim45.html
Also, here are two YouTube videos that do a great job of breaking down frames of reference so that they can be easily understood:
https://www.youtube.com/watch?v=mYH_nODWkqk
https://www.youtube.com/watch?v=jYMU6bn5GHY
Examples
Simple
Say that you are pulled over on the side of the road and a car passes by you at a speed of 50 m/s. You then start to drive at a speed of 43 m/s and you see the car that just drove by in from of you. What is the speed of the car from your moving frame of reference?
As we know,
[math]\displaystyle{ \vec{v} = \vec{v}' + \vec{v}_{frame} }[/math]
In this scenario, [math]\displaystyle{ \vec{v} = 50 m/s }[/math] since that is the velocity from our initial stationary reference frame. [math]\displaystyle{ \vec{v}_{frame} = 43 m/s }[/math] because that is now the velocity of our frame of reference, meaning that [math]\displaystyle{ \vec{v}' }[/math] is what we are solving for.
Plugging in what we know, [math]\displaystyle{ 50 m/s = 43 m/s + \vec{v}' }[/math]
This means that [math]\displaystyle{ \vec{v}' = 7 m/s }[/math]
Middling
You are in a boat and you see another boat that to you think is moving at a velocity of <5,17,0> m/s. Your friend who is stationary on the shore thinks that it is moving at a velocity of <10, 24,0> m/s. What is the velocity of your boat?
[math]\displaystyle{ \vec{v} = \vec{v}' + \vec{v}_{frame} }[/math]
In this scenario, [math]\displaystyle{ \vec{v}_{frame} }[/math]is what we are solving for and [math]\displaystyle{ \vec{v}' }[/math] = <5,17,0> m/s, meaning that [math]\displaystyle{ \vec{v} }[/math] is <10, 24,0> m/s.
Plugging in what we know, [math]\displaystyle{ \lt 10, 24,0\gt m/s = \lt 5,17,0\gt m/s + \vec{v}_{frame} }[/math]
This means that [math]\displaystyle{ \vec{v}_{frame} = \lt 5,7,0\gt m/s }[/math]
Difficult
You are in an airplane and you travel a distance of <480,140,620> meters in 8 seconds. You see a plane below you and to you it looks like it has a velocity of <50,23,62> m/s. What would the velocity of the second plane be to a stationary observer?
As we know,
[math]\displaystyle{ Δx = v * t }[/math]
[math]\displaystyle{ Δx = \lt 480,140,620\gt meters }[/math]
[math]\displaystyle{ t = 8 seconds }[/math]
Therefore,
[math]\displaystyle{ v = \lt 60,17.5,77.5\gt m /s }[/math]
Also,
[math]\displaystyle{ \vec{v} = \vec{v}' + \vec{v}_{frame} }[/math]
In this scenario, [math]\displaystyle{ \vec{v}_{frame} = \lt 60,17.5,77.5\gt m /s }[/math] and [math]\displaystyle{ \vec{v}' = \lt 50,23,62\gt }[/math], meaning that [math]\displaystyle{ \vec{v} }[/math] is what we are solving for.
Plugging in what we know, [math]\displaystyle{ \vec{v} = \lt 60,17.5,77.5\gt m/s + \lt 50,23,62\gt m/s }[/math]
This means that [math]\displaystyle{ \vec{v} = \lt 110,40.5,139.5\gt m/s }[/math]
Reference Frame in Special Relativity

The first postulate of the theory of Einstein's Theory of Special Relativity states that the laws of physics always hold true for all reference frames. while the second postulate of the theory of special relativity states that the speed of light is constant in all of the reference frames. Thus in order for both of them to be true Time Dilation [math]\displaystyle{ \Delta t' = \frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}} \, }[/math] and lengths contraction :[math]\displaystyle{ \ L = {Lo}{\sqrt{1-\frac{v^2}{c^2}}} \, }[/math] Where [math]\displaystyle{ \gamma = \left ( \sqrt{1 - \frac{v^2}{c^2}}\right )^{-1} }[/math] are required to satisfy the two postulates. Thus we known that in relativity theory time and lengths depends on your reference frame making the simple calculation of [math]\displaystyle{ \vec{v} = \vec{v}' + \vec{v}_{frame} }[/math] not true. This change in time and length makes the coordinates for each reference frame different.
Lorentz Transformation

The needed transformation for coordinates in special relativity are called Lorentz Transformations named after the dutch physicist Hendrik Lorentz. These transformations makes it possible to calculate the velocity, time, and position for different frame of references.
[math]\displaystyle{ \begin{align} t' &= \gamma \left( t - \frac{vx}{c^2} \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end{align} }[/math] where [math]\displaystyle{ (t, x, y, z) }[/math] and [math]\displaystyle{ (t', x', y', z') }[/math] are the coordinates of an event in two frames with the same origin point [math]\displaystyle{ t=t'=0 }[/math] Although Lorentz Transformation is very effective in the inertial reference frame (Relative movement with constant velocity) Lorentz Transformation can't be used for non-inertial reference frames. Even though you can do some vectors transformations to use it with different angles.
[math]\displaystyle{ \begin{align} t' &= \gamma \left(t - \frac{\mathbf{r}_\parallel \cdot \mathbf{v}}{c^2} \right) \\ \mathbf{r}_\|' &= \gamma (\mathbf{r}_\| - \mathbf{v} t) \\ \mathbf{r}_\perp' &= \mathbf{r}_\perp \end{align} }[/math]
Doppler Effect

The Doppler effect or Doppler shift is the change in frequency of the wave in relation to an observer whom is moving relative to the source wave. This change is apparent in sound waves where a car is moving toward you with sirens you notice a difference in sound compared to when it's moving away from you. At speeds that are close to the speed of light, this change happens for light too so the observed light is different than the frequency emitted by the source. The reason for this effect is that the beginning of each wave is emitted closer than if the source was standing still thus giving the wave different characteristics.
This phenomenon is very apparent in the redshift where the background radiation emitted from the heat of the particles in the universe gives a different frequency than the one calculated in particular it is red shifted. And from this and doppler shift they concluded that the universe is expanding thus these particles are moving away.
Connectedness
- I have always been interested in how we perceive the world around us and take measurements. It had never occurred to me that something as simple as speed could change based on the observer and so researching and understanding this topic proved to be very fun and interesting.
- This topic has nothing to do with my current major of Computer Science.
- Analyzing frames of reference can provide many key insights in industrial settings. Whether it be looking at colliding particles in the LHC or why the speed of light is the absolute speed limit of the universe, looking at these things can help scientists understand the world around us and hopefully make great inventions based of these results.
History

Although it is not known who came up with this concept of reference frames, it has been key to interpreting and understanding the world around us. Newton assumed a Euclidean space when looking at frames of reference which he used when he came up with important ideas and theories such as gravity. Einstein came up with transformations between reference frames to come up with his special theory of relativity. These are just some examples of how frames of reference have been used through the history of science and man.
See also
Relevant Materials
Further reading
Matter and Interactions Fourth Edition By Ruth W. Chabay, Bruce A. Sherwood - Chapter 10 Section 5
External links
- 1: https://www.youtube.com/watch?v=mYH_nODWkqk
- 2: https://www.youtube.com/watch?v=jYMU6bn5GHY
- 3: http://www.wiley.com/college/halliday/0470469080/simulations/sim45/sim45.html
- 4: https://www.khanacademy.org/science/physics/forces-newtons-laws/newtons-laws-of-motion/v/newton-s-first-law-of-motion
References
- 1: Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.
- 2: "Frames of Reference." Isaac Physics. N.p., n.d. Web. <https://isaacphysics.org/concepts/cp_frame_reference>.
- 3: "Reference Frame." Everthing Maths & Science. N.p., n.d. Web. <http://www.everythingmaths.co.za/science/grade-10/21-motion-in-one-dimension/21-motion-in-one-dimension-02.cnxmlplus>.
- 4: Wikipedia. Wikimedia Foundation, n.d. Web. <https://en.wikipedia.org/wiki/Frame_of_reference#Remarks>.
- 5: Wikipedia. Wikimedia Foundation, n.d. Web. <https://en.wikipedia.org/wiki/Inertial_frame_of_reference>.