Inertia

Created by Matthew Thomas Erickson, Fall 2024

This page defines and describes inertia.

All Khan Academy content is available for free at www.khanacademy.org

The Main Idea

Inertia, a fundamental concept in physics, is the tendency of an object to resist changes in its state of motion or rest. It is closely tied to Newton's First Law of Motion, often called the Law of Inertia, which states that an object will remain at rest or in uniform motion unless acted upon by an external force. Understanding inertia is crucial because it forms the foundation for analyzing motion and forces in our everyday world, from why we feel a jolt in a car when it suddenly stops to how satellites maintain their orbits in space. Recognizing the role of inertia allows engineers, scientists, and innovators to design safer vehicles, more efficient machines, and technologies that harness or counteract these natural tendencies.

Inertia encompasses several subtopics that expand its importance in various fields of physics and engineering. One key aspect is the relationship between mass and inertia; an object’s resistance to motion is directly proportional to its mass. Rotational inertia, or the resistance of an object to changes in its rotational motion, introduces concepts like torque and total angular momentum, critical for understanding everything from spinning figure skaters to the stability of spacecraft. Additionally, the concept of moment of inertia, a quantitative measure of rotational resistance, is essential in mechanical design and structural engineering. By studying inertia, we not only gain insights into the principles governing motion but also unlock tools for solving real-world problems across multiple disciplines.

A Mathematical Model

Simply, According to Newton's Second Law: the Momentum Principle, [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math]. The more massive an object is, the less its velocity needs to change in order to achieve the same change in momentum in a given time interval.

The other form of Newton's Second Law is [math]\displaystyle{ \vec{F}_{net} = m \vec{a} }[/math]. Solving for acceleration yields [math]\displaystyle{ \vec{a} = \frac{\vec{F}_{net}}{m} }[/math]. This shows the inverse relationship between mass and acceleration for a given net force.

However, the concept of inertia is used more commonly in reference to rotational applications. In rotational dynamics, inertia takes on an additional layer of complexity. The moment of inertia, 𝐼, quantifies an object's resistance to changes in rotational motion and depends not only on the object's mass but also on how that mass is distributed relative to the axis of rotation. The formula τ=Iα, where τ is torque and α is angular acceleration, mirrors the linear motion equation F=ma, connecting rotational resistance to real-world applications. For instance, the moment of inertia is a critical parameter in designing flywheels, turbines, and gears, where precise control of rotational motion is necessary. Furthermore, in systems like pendulums or oscillating objects, the interplay between inertia and restoring forces leads to equations of motion that can be solved using calculus, providing insights into periodic motion and energy conservation. These mathematical tools not only deepen our understanding of inertia but also enable practical solutions in diverse fields like aerospace engineering, robotics, and biomechanics.

How to Approach a Problem

Understand the Problem Statement
- Carefully read the problem and identify the given information and what you need to find.
- Look for keywords that indicate linear motion, rotational motion, momentum, or forces, such as "mass," "velocity," "force," "impulse," or "torque."
Identify the Relevant Concepts
- Determine if the problem involves linear motion, rotational motion, or a combination of both.
- Decide if you need to apply the concepts of inertia (resistance to motion) or momentum ([math]\displaystyle{ p=mv }[/math] for linear momentum or [math]\displaystyle{ L=Iω }[/math] for angular momentum).
Draw a Diagram
- Sketch a free-body diagram (for forces) or a simple representation of the system.
- Indicate the direction of forces, motion, or velocities. Label axes to establish a clear reference frame.
Write Down Known Equations
- For linear motion:
  - [math]\displaystyle{ F=ma }[/math],
  - [math]\displaystyle{ p=mv }[/math],
  - [math]\displaystyle{ Δp=FΔt }[/math] (impulse-momentum theorem).
- For rotational motion:
  - [math]\displaystyle{ τ=Iα }[/math],
  - [math]\displaystyle{ L=Iω }[/math],
  - [math]\displaystyle{ ΔL=τΔt }[/math].
- Include energy-related equations if necessary:
  - [math]\displaystyle{ KE= 1/2mv^2 }[/math] (linear)
  - [math]\displaystyle{ KE= 1/2Iω^2 }[/math] (rotational).
Substitute Known Values
- Plug the given values into the appropriate equations. Be mindful of units and convert them if necessary.
- Simplify the equations to isolate the variable you are solving for.
Apply Conservation Laws (if applicable)
- Use the conservation of linear momentum ([math]\displaystyle{ p_initial = p_final }[/math]) or angular momentum ([math]\displaystyle{ L_initial=L_final }[/math]) if the problem involves collisions, explosions, or systems with no external forces/torques.
- If energy is conserved, consider [math]\displaystyle{ KE_initial + PE_initial = KE_final + PE_final }[/math].
Solve Mathematically
- Solve the equations step-by-step. Keep the calculations clean and track units to ensure accuracy.
Analyze Your Results
- Check if your solution is physically reasonable (e.g., does the velocity, force, or momentum make sense for the scenario?).
- Confirm that the units of your final answer match the quantity you're solving for.
Refine for Multiple Parts
- If the problem has multiple parts, use the results of earlier calculations to address subsequent parts.
- Revisit the concepts if you encounter new conditions (e.g., friction, non-constant forces).

A Computational Model

Here is a link to a computational model that can aid in better understanding inertia. [1] The situation shown is very similar to that described in the "Industry Applications" portion of this page.

Here are snapshots from a similar model:

Inertial Reference Frames

In physics, properties such as objects' positions, velocities, and accelerations depend on the Frame of Reference used. Different reference frames can have different origins, and can even move and accelerate with respect to one another. According to Einstein's idea of relativity, one cannot tell the position or velocity of one's reference frame by performing experiments. For example, a person standing in an elevator with no windows cannot tell if it is moving up or down by, say, dropping a ball from shoulder height and measuring how long it takes to hit the ground. The answer will be the same regardless of the velocity of the elevator, in part because when the ball is released from shoulder height, it is travelling at the same velocity as the elevator. However, one can tell the acceleration of one's reference frame by performing experiments. For example, if a person standing in an elevator with no windows were to drop a ball from shoulder height, if the elevator were accelerating upwards, it would take less time for the ball to hit the ground than if the elevator were moving at a constant velocity. This is because the ground accelerates towards the ball. From the point of view of the person in the elevator, the ball would appear to violate Newton's second law; it would appear to accelerate towards the ground faster than accounted for by the force of gravity. This is because Newton's second law was written for inertial reference frames. An inertial reference frame is a reference frame travelling at a constant velocity. The physics in this course is true only in inertial reference frames, and problems in this course should be solved using inertial reference frames. The surface of the earth is usually considered an inertial reference frame; its rotations about its axis and revolutions around the sun are technically forms of acceleration, but both are so small that they have negligible effects on most aspects of motion. The definition of an inertial reference frame is one in which matter exhibits inertia; in accelerating reference frames, objects may accelerate despite the absence of external forces acting on them.

Examples

Simple

Find the mass of an object whose acceleration is 4 m/s^2 and whose translational inertia is 20 kg.

[math]\displaystyle{ T = ma }[/math]

Where T is translational inertia, m is mass, and a is acceleration.

[math]\displaystyle{ m = \frac{T}{a} }[/math]

[math]\displaystyle{ m = \frac{20 kg}{4 m/s^2} }[/math]

[math]\displaystyle{ m = 5 kg }[/math]

Middling

A motor capable of producing a constant torque of 100 Nm and a maximum rotation speed of 150 rad/s is connected to a flywheel with rotational inertia 0.1 kgm^2

a) What angular acceleration will the flywheel experience as the motor is switched on?

[math]\displaystyle{ \tau = I\alpha }[/math]

Where [math]\displaystyle{ \tau }[/math] is torque, I is rotational inertia, and [math]\displaystyle{ \alpha }[/math] is angular acceleration.

[math]\displaystyle{ \alpha = \frac{\tau}{I} }[/math]

[math]\displaystyle{ \alpha = \frac{100 Nm}{0.1 kgm^2} }[/math]

[math]\displaystyle{ \alpha = 1000 rad/s^2 }[/math]

b) How long will the flywheel take to reach a steady speed if starting from rest?

Using rotational kinematics,

[math]\displaystyle{ \omega = \omega_0 + \alpha \times t }[/math]

Since we know the maximum rotational velocity of the motor, we can solve to find the time taken to accelerate up to that rotational velocity.

[math]\displaystyle{ t = \frac{{\omega}_{max}}{\alpha} }[/math]

[math]\displaystyle{ t = \frac{150 rad/s}{1000 rad/s^2} }[/math]

[math]\displaystyle{ t = 0.15 s }[/math]

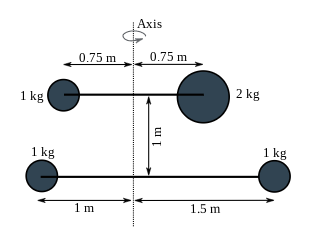
Difficult

What is the rotational inertia of the object shown above?

[math]\displaystyle{ I = m_1r_1^2 + m_2r_2^2 + ... = \sum m_ir_i^2 }[/math]

Where I is rotational inertia, m is mass, and r is distance from the axis of rotation.

[math]\displaystyle{ I = (1 kg \times 1^2 m^2) + (1 kg \times 1.5^2 m^2) + (1 kg \times 0.75^2 m^2) + (2 kg \times 0.75^2 m^2) }[/math]

[math]\displaystyle{ I = 4.9375 kgm^2 }[/math]

Connectedness

Interesting Applications

Scenario: Tablecloth Party Trick

A classic demonstration of inertia is a party trick in which a tablecloth is yanked out from underneath an assortment of dinnerware, which barely moves and remains on the table. The tablecloth accelerates because a strong external force- a person's arm- acts on it, but the only force acting on the dinnerware is kinetic friction with the sliding tablecloth. This force is significantly weaker, and if the tablecloth is pulled quickly enough, does not have enough time to impart a significant impulse on the dinnerware. This trick demonstrates the inertia of the dinnerware, which has an initial velocity of 0 and resists change in velocity.

Scenario: Turning car

You have probably experienced a situation in which you were driving or riding in a car when the driver takes a sharp turn. As a result, you were pressed against the side of the car to the outside of the turn. This is the result of your inertia; when the car changed direction, your body's natural tendency to continue moving in a straight line caused it to collide with the side of the car (or your seatbelt), which then applied enough normal force to cause your body to turn along with the car.

Connection to Mathematics

Inertia is studied using Newton's Second Law, which states that [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math]. The [math]\displaystyle{ \frac{d\vec{p}}{dt} }[/math] in this equation stands for the derivative of momentum.

Derivatives are core concept of a branch of Mathematics called Calculus, which studies constant motion. In this way, understanding inertia gives one a deeper understanding of Calculus, which is an integral member of the Mathematics family.

Industry Application

Using a seat belt is one of the best methods for preserving one's life in the event of a car crash. For this reason, they are a big deal in the vehicular safety industry.

Passengers in a moving car have the same motion as the car they are in. When that car stops abruptly, as cars often do in the event of a car crash, its passengers do not stop. Instead, they continue to have the same motion that the car did before it stopped because of inertia. This motion can often propel passengers of out the car, which increases the likelihood of death.

Seat belts are designed to fight against inertia and hold passengers in their seats, often saving their lives in the process.

History

Before Newton's Laws of Motion came to prominence, models of motion were based on of the observation that objects on Earth always ended up in a resting state regardless of their mass and initial velocity. Today we know this belief to be the result of Friction. Since friction is present for all macroscopic motion on earth, it was difficult for academics of the time to imagine that motion could exist without it, so it was not separated from the general motion of objects. However, this posed a problem: the perpetual motion of planets and other celestial bodies. Galileo Galilei (1564-1642) was the first to propose that perpetual motion was actually the natural state of objects, and that forces such as friction were necessary to bring them to rest or otherwise change their velocities.

Galileo performed an experiment with two ramps and a bronze ball. The two ramps were set up at the same angle of incline, facing each other. Galileo observed that if a ball was released on one of the ramps from a certain height, it would roll down that ramp and up the other and reach that same height. He then experimented with altering the angle of the second ramp. He observed that even when the second ramp was less steep than the first, the ball would reach the same height it was dropped from. (Today, this is known to be the result of conservation of energy.) Galileo reasoned that if the second ramp were removed entirely, and the ball rolled down the first ramp and onto a flat surface, it would never be able to reach the height it was dropped from, and would therefore never stop moving if conditions were ideal. This led to his idea of inertia.

References