The Moments of Inertia
Claim By Prajwal Saokar Fall 2025
claimed and written by san47
Main Idea
Moment of inertia, or Rotational Inertia, is denoted in mechanics by the letter I. It is a quantity which describes the relationship between an object's angular momunetum and it's angular velocity. In physical terms, it could be percieved as a measure of how "difficult" it is to rotate an object at a given angular velocity, and is derived from the physical characteristics of the object, specifically it's mass distribution about the axis of rotation. [2][3]
A Mathematical Model

The moment of inertia for a point particle is characterized by the mass of the particle multiplied by the perpindicular radius to the axis of rotation squared, as shown below:
- [math]\displaystyle{ I = mr^2 }[/math]
Using this equivalence, it is actually possible to show that the two formulations of angular momentum are equivalent for point particles as well as for continuous masses. For point particles, the proof is quite straightforward:
We start by knowing that:
[math]\displaystyle{ \vec{L} = \vec{r}\times\vec{p} }[/math]
and
[math]\displaystyle{ \vec{L} = I\vec{\omega} }[/math]
We can now substitute in our expression for I:
[math]\displaystyle{ \vec{L} = mr^2\vec{\omega} }[/math]
We can also simplify our first definition of angular momentum by evaluating the cross product. Since the particle is rotating,[math]\displaystyle{ \vec{r} }[/math] is by definition perpendicular to [math]\displaystyle{ \vec{p} }[/math], so we arrive at:
[math]\displaystyle{ \vec{L} = \vec{r}\times\vec{p} = rmv\hat{z} }[/math]
where [math]\displaystyle{ \hat{z} }[/math] is simply the direction perpendicular to both [math]\displaystyle{ \vec{r} }[/math] and [math]\displaystyle{ \vec{p} }[/math].
Finally, by noting that [math]\displaystyle{ \omega = \frac{v}{r} }[/math], we can show:
[math]\displaystyle{ \vec{L} = mr^2\vec{\omega} = mr^2\frac{v}{r} = mvr\hat{z} }[/math]
In doing this, we have shown that the "spin" formulation of angular momentum often used for continuous masses is simply a reformulation of the translational formulation which is used to describe point particles.
Extended Masses
In the same way that angular momentum could be extended to continuous masses and multiparticle systems, so can the rotational inertia of an object. In fact, it is this extension that gives us the "spin" formulation of angular momentum in the first place
For any extended mass, the rotational inertia can be calculated by taking the limit of the summation used for multiparticle systems as each [math]\displaystyle{ m_j }[/math] approaches 0, filling some finite volume with infinitely many of these [math]\displaystyle{ m_j }[/math] terms:
[math]\displaystyle{ I = \sum_{j=1}^n m_jr_j^2 }[/math]
[math]\displaystyle{ I = \lim_{m_j \to 0} \sum_{j=1}^\infty m_jr_j^2 }[/math]
[math]\displaystyle{ I = \int_M r^2 dm }[/math]
which can be rewritten in terms of density and volume as:
[math]\displaystyle{ I = \iiint_V \rho(x, y, z) r^2 dV }[/math]
Calculating Moment of Inertia
Thin Rod
Divide into Small Slices Divide the rod into N small slices of equal length [math]\displaystyle{ \Delta x = L/N }[/math], each with mass of [math]\displaystyle{ \Delta M = M/N }[/math].
The Mass of One Slice Concentrate on one representative slice: [math]\displaystyle{ N = L/\Delta x }[/math] so that [math]\displaystyle{ \Delta M = M/N = M(\Delta x/L) }[/math].
The Contribution of One Slice Approximation [math]\displaystyle{ r_\perp \approx x_n }[/math]: [math]\displaystyle{ \Delta I=(\Delta M)x^2 _n = (M/L)x^2 _n\Delta x. }[/math]
Adding Up the Contributions [math]\displaystyle{ I = \sum_{n=1}^N \Delta I = (M/L)\sum_{n=1}^N x^2 _n\Delta x }[/math].
The Finite Sum Becomes a Definite Integral [math]\displaystyle{ I = (M/L) \lim_{N \to \infty}\sum_{n=1}^N x^2 _n\Delta x }[/math] [math]\displaystyle{ = (M/L) \int\limits_{x_i}^{x_f}x^2\, dx }[/math].
The Limits of Integration Since the origin was at the center of the rod: [math]\displaystyle{ I = (M/L) \int\limits_{-L/2}^{+L/2}x^2\, dx = (1/12)ML^2 }[/math].
Hoop
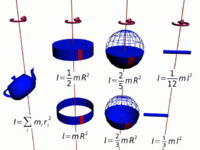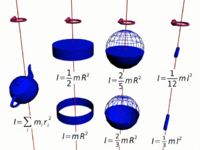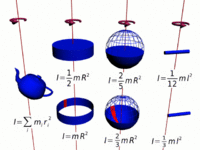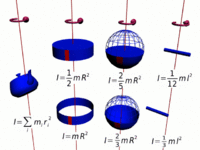
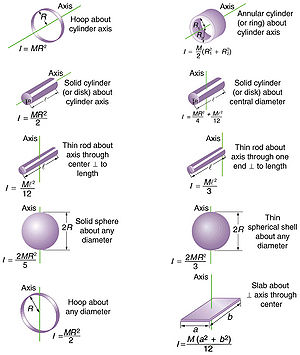
The moment of inertia of a hoop or thin hollow cylinder of negligible thickness about its central axis is a straightforward extension of the moment of inertia of a point mass since all of the mass is at the same distance R from the central axis.[4]
Sphere
The moment of inertia of a sphere can be expressed as the summation of moments of infinitesimally thin disks about the z axis.

Cylinder
The moment of inertia of a solid cylinder can be calculated from the built up of moment of inertia of thin cylindrical shells. [6] Because only the perpendicular distances of atoms from the axis matter([math]\displaystyle{ r_\perp }[/math]), the moment of inertia for rotation about the axis of a long cylinder has exactly the same form as that of a disk. It means that the moment of inertia does not matter how long the cylinder is or how thick the disk is.
Other
The moments of inertia for different shapes can be calculated by applying integral calculus as shown in the calculation of moment of inertia for the Thin Rod or sphere.
Examples
Simple
What is the moment of inertia of a diatomic nitrogen molecule [math]\displaystyle{ N_2 }[/math] around its center of mass? The mass of a nitrogen atom is [math]\displaystyle{ 2.3 \times 10^{-26} kg }[/math] and the average distance between nuclei is [math]\displaystyle{ 1.5 \times 10^{-10} m. }[/math] Use the definition of moment of inertia carefully.
Solution
For two masses, [math]\displaystyle{ I = m_1r^2 {_\perp,_1} + m_2r^2 {_\perp,_2} }[/math]. The distance between masses is d, so the distance of each object from the center of mass is [math]\displaystyle{ r{_\perp,1} = r{_\perp,2} = (d/2) }[/math]. Therefore
- [math]\displaystyle{ I = M(d/2)^2 + M(d/2)^2 = 2M(d/2)^2 }[/math]
- [math]\displaystyle{ I = 2 \cdot (2.3 \times 10^{-26} kg)(0.75 \times 10^{-10} m)^2 }[/math]
- [math]\displaystyle{ I = 2.6 \times 10^{-46} kg \cdot m^2 }[/math]
Medium
Imagine a 0.002 kg ladybug resting on the edge of a spinning disk. If the mass of the disk is 2 kg and it has a radius of 0.15m, what is the combined rotational inertia of the disk and the ladybug about the center of the disk (hint: treat the ladybug as a point mass)?
Solution
In order to solve this problem, we can write out the combined rotational inertia in terms of it's constituent parts:
[math]\displaystyle{ I_{tot} = I_{L} + I_{disk} }[/math]
In this case, we can treat the ladybug as a point mass resting at the edge of the disk, so we have:
[math]\displaystyle{ I_{L} = M_{L}R_{disk}^2 }[/math]
[math]\displaystyle{ I_L = 0.002(0.15)^2 }[/math]
[math]\displaystyle{ I_L = 4.5 x 10^{-5} kg \cdot m^2 }[/math]
Next we calculate the rotational inertia of the disk. As this is an often used object, we know that the rotational inertia of a disk is given by:
[math]\displaystyle{ I_{disk} = \frac{1}{2}M_{disk}R_{disk}^2 }[/math]
[math]\displaystyle{ I_{disk} = \frac{1}{2}(2)(0.15)^2 }[/math]
[math]\displaystyle{ I_{disk} = 2.25 x 10^{-2} kg \cdot m^2 }[/math]
Finally, we have:
[math]\displaystyle{ I_{tot} = 2.2545 x 10^{-2} kg \cdot m^2 }[/math]
So, we see that in this case the added rotational inertia of the ladybug is negligible compared to the rotational inertia of the disk.
Difficult
Derive the equation for the rotational inertia of a sphere of mass [math]\displaystyle{ m }[/math] and radius [math]\displaystyle{ r }[/math] about one of its internal axes. Do this by using the definition of rotational inertia for continuous masses. (Also solve the Riemann Hypothesis)
Solution
In order to solve this problem, we can start by splitting the sphere into smaller objects of known rotational inertia. In this case, the sphere is made up of infinitely many infinitely small disks each centered on the axis of rotation. We know that:
[math]\displaystyle{ I_{disk} = \frac{1}{2}M_{disk}R_{disk}^2 }[/math]
We then need to sum together the rotational inertia contributions for each of these spheres. Treating, the mass of each infintesimal disk as some [math]\displaystyle{ dm }[/math] we have:
[math]\displaystyle{ I_{sphere} = \frac{1}{2}\int_{-r}^{r} R_{disk}^2 dm }[/math]
Now, we can express [math]\displaystyle{ dm }[/math] in terms of the mass and radius of the sphere by using the mass density of the sphere:
[math]\displaystyle{ dm = \rho_{sphere}V_{disk} = \rho_{sphere}\pi R_{disk}^2 dz }[/math]
Using trigonometry, we obtain:
[math]\displaystyle{ R_{disk}^2 = r^2 - z^2 }[/math]
So therefore:
[math]\displaystyle{ dm = \rho_{sphere}\pi(r^2 - z^2) dz }[/math]
We also know that since the sphere has uniform mass density, we have:
[math]\displaystyle{ \rho_{sphere} = \frac{m}{\frac{4}{3} \pi r^3} }[/math]
[math]\displaystyle{ dm = \frac{m}{\frac{4}{3} \pi r^3}\pi(r^2 - z^2) dz }[/math]
Now, substituting back into the integral and cancelling terms, we arrive at:
[math]\displaystyle{ I_{sphere} = \frac{1}{2}\frac{m}{\frac{4}{3} \pi r^3}\pi \int_{-r}^{r} (r^2 - z^2)^2 dz }[/math]
[math]\displaystyle{ I_{sphere} = \frac{m}{\frac{8}{3} r^3} \int_{-r}^{r} (r^2 - z^2)^2 dz }[/math]
Evaluating the integral, we get:
[math]\displaystyle{ I_{sphere} = \frac{m}{\frac{8}{3} r^3} (\frac{16r^5}{15}) }[/math]
and finally, we arrive at:
[math]\displaystyle{ I_{sphere} = \frac{2}{5}mr^2 }[/math]
See also
External links
http://www.bsharp.org/physics/spins
http://www.real-world-physics-problems.com/physics-of-figure-skating.html
References
- Nave, R. "Concepts" HyperPhysics. Web.
- Nave, R. "Moment of Inertia" HyperPhysics. Web.
- Urone, Paul Peter., Roger Hinrichs, Kim Dirks, and Manjula Sharma. "Rotational Inertia and Moment of Inertia." College Physics. Houston, TX: OpenStax College, Rice U, 2013. 354. Print.
- Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Modern Mechanics. Hoboken, NJ: Wiley, 2011. Print.
- http://www.hunter.cuny.edu/physics/courses/physics110/repository/files/Giancoli_Prob.Solution%20Chap.8.pdf