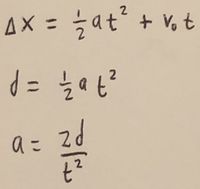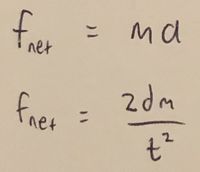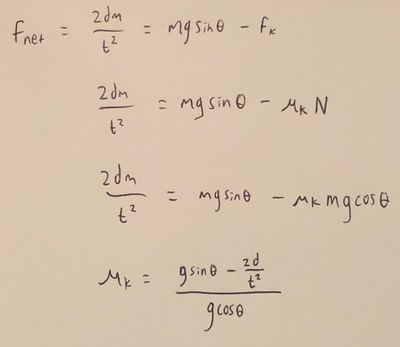Friction
This page describes several types of friction and explains how they affect systems.
The Main Idea
Friction is a force that resists movement between surfaces in contact. It is caused by the interactions between the molecules that make up objects. There are three types of friction: Static Friction, which resists motion between surfaces that are not moving with respect to each other at their point of contact; Kinetic Friction, which resists motion between surfaces that are moving with respect to each other at their point of contact; and fluid friction, which resists the motion of bodies moving through gases and liquids. All types of friction depend on the materials comprising the surfaces of the objects and substances involved, as well as on the normal force they exert on each other (that is, the force with which they are pressed together).
- Static Friction When two objects touch each other and there is no sliding between their surfaces of contact, they exert static friction forces on each other. The static friction force acting on each object opposes any force that would cause it to slide relative to the other object. For example, consider a heavy dresser at rest on the floor. If a child pushes against the side of the dresser in an attempt to slide it, that exerts a force on the dresser, but the ground would exert on it an equal and opposite static friction force that balances the force exerted by the child, so the dresser stays at rest. The static friction force can take on whatever direction and magnitude necessary to balance an external net force that threatens to cause sliding motion between two surfaces. However, the magnitude of the static friction force is limited by a maximum value. If the external force becomes strong enough, the static friction force can be overcome and the surfaces can begin to slide, at which point the friction between the objects becomes kinetic. For example, now consider an adult pushing against the same heavy dresser. The adult can exert a stronger force than the child, and if it exceeds the maximum possible static friction force, the dresser can be set into motion and slid across the floor. Note that static friction is present between rolling objects and the surface on which they roll. For more information, see the "Static Friction on Rolling Objects" section on the Static Friction page, as well as the Rolling Motion page.
- Kinetic Friction When two objects touch each other and there is sliding between their surfaces of contact, they exert a kinetic friction force on each other. The kinetic friction force acting on each object acts in a direction opposite to its direction of motion relative to the other object. If the kinetic friction force is the only force acting on each object, they will eventually come to rest relative to each other, at which point the friction force between them becomes static. For example, consider a crate sliding across the floor. It will slow down and eventually come to rest due to the kinetic friction force between it and the floor, unless another force acts on it, such as the pushing of a person that wants to keep the crate moving. Kinetic friction force within a system lowers the system's kinetic energy, converting it to Thermal Energy. In other words, sliding between surfaces causes the surfaces to heat up. Usually in mechanical physics, this thermal energy is no longer considered part of the system and is considered lost because it usually dissipates into the environment without ever being converted back into mechanical energy. This means kinetic friction does negative work on the system. In addition to dissipating energy as thermal energy, kinetic friction may also dissipate a smaller amount of energy as sound, and can wear down surfaces if sufficiently intense.
- Fluid friction When an object moves through a liquid or gas, the fluid exerts a force on the object in the direction opposite to its motion relative to the fluid. Air Resistance is one common example of fluid friction that can affect the motion of projectiles and other objects in the earth's atmosphere. In many problems, you are asked to assume that the effects of air resistance are negligible because it is often not as strong as other forces and can significantly complicate math. However, the force exerted on an object by air resistance can be significant depending on the mass and geometry of the object, and the fluid friction exerted by thicker fluids such as water are almost always significant. Fluid friction, like kinetic friction, causes the conversion of energy from kinetic to thermal.
Friction between surfaces is largely the result of adhesive forces between them that must be overcome to move them. All surfaces are rough on a microscopic level, so when two surfaces are pressed against each other, they form only a few points of contact. At these points of contact, the molecules of each surface are attracted to the molecules of the other due to several types of inter-molecular forces. The greater the normal force between the surfaces (that is, the harder they are pressed together), the greater the number and size of these points of contact, and therefore, the greater the friction force between them. In addition to these adhesive forces, friction is also caused in part by deformation that occurs when materials are pressed together. Both of these mechanisms contribute to the conversion of kinetic energy to thermal energy; the molecules' interactions channel the kinetic energy of the macroscopic objects into the kinetic energy of individual molecules. Tribology, or the study of friction, is still an active area of research today.
Often, friction is thought of as opposing all motion. In reality, it opposes the relative motion between objects or substances, which can in some situations actually cause motion. For example, consider a person who starts at rest and begins to walk. In order to walk, the person's foot must push off of the ground. In the absence of static friction, which is nearly the case on an ice skating rink, the shoe would slip across the ground without pushing off; it is only because static friction opposes the relative motion between the person's foot and the ground that they are able to begin moving. Similarly, consider a stationary object placed onto a moving conveyor belt. There would be kinetic friction between the object and the belt, causing the object to accelerate until it reaches the velocity of the belt. Finally, consider a river sweeping away a log that was initially at rest. The log was initially at rest relative to the riverbank, but relative to the running water, it was moving! Fluid friction is what opposed this relative motion, bringing the log to the velocity of the river water. In each of these examples, motion is caused by friction.
A Mathematical Model
These formulas give the magnitudes of each kind of friction.
- Static Friction As described above, the magnitude of the static friction force ([math]\displaystyle{ F_s }[/math]) between two objects is bounded by a maximum value. For most problems involving static friction it is necessary to find this maximum static friction force. Its value is given by [math]\displaystyle{ F_{s, max} = \mu_s * N }[/math] where [math]\displaystyle{ \mu_s }[/math] is the coefficient of static friction of the objects and [math]\displaystyle{ N }[/math] is the normal force between the objects. [math]\displaystyle{ \mu_s }[/math] is a property of the materials of the surfaces in contact and is usually less than 1. [math]\displaystyle{ \mu_s }[/math] has no units because it is a ratio of one force to another. This formula may also be written [math]\displaystyle{ F_s \leq \mu_s * N }[/math].
- Kinetic Friction The magnitude of the kinetic friction force between objects is given by [math]\displaystyle{ F_k = \mu_k * N }[/math] where [math]\displaystyle{ \mu_k }[/math] is the coefficient of kinetic friction of the objects and [math]\displaystyle{ N }[/math] is the normal force between the objects. [math]\displaystyle{ \mu_k }[/math] is a property of the materials of the surfaces in contact and is usually less than 1. [math]\displaystyle{ \mu_k }[/math] has no units because it is a ratio of one force to another. For any given pair of surfaces, their [math]\displaystyle{ \mu_s }[/math] value is greater than their [math]\displaystyle{ \mu_k }[/math] value. Note that this formula indicates that the magnitude of the kinetic friction force does not depend on the speed of the sliding between the objects.
- Fluid Friction The magnitude of the fluid friction force acting on an object moving through a fluid is given by [math]\displaystyle{ F_{fl} = b * v }[/math], where [math]\displaystyle{ b }[/math] is the drag coefficient and [math]\displaystyle{ v }[/math] is the speed of the object relative to the fluid. The drag coefficient depends on the geometry of the object as well as the viscosity (thickness) of the fluid. Consider an object of mass [math]\displaystyle{ m }[/math] given an initial velocity [math]\displaystyle{ v_0 }[/math] through a fluid. Its drag coefficient is [math]\displaystyle{ b }[/math]. If fluid friction is the only force acting on it, the following differential equation can be derived from the formula above along with Newton's second law: [math]\displaystyle{ \frac{dv}{dt} = -\frac{bv}{m} }[/math]. This is a separable differential equation, and solving it yields [math]\displaystyle{ v = v_0 e^{-\frac{b}{m}t} }[/math], showing that the velocity of an object moving through a fluid exponentially decays if no other forces act on it. Another concept worth exploring regarding fluid friction is terminal velocity. See Terminal Velocity and Friction Due to Air. Note: in some scenarios, the magnitude of the fluid friction force acting on an object is more nearly proportional to the square of the object's velocity than to the object's velocity itself, but that model of fluid friction lies outside the scope of this page.
A Computational Model
- Static Friction This is a VPython simulation of a box held in place by static friction. A steadily increasing external force, shown by the green arrow, is balanced by an equal and opposite static friction force, until the magnitude of the external force exceeds [math]\displaystyle{ \mu_s * N }[/math]. At this time, the box begins to move and the friction becomes kinetic. Static friction simulation Click "View this program" on the top left corner to view the VPython code.
- Kinetic Friction This is a VPython simulation of a box sliding along a surface. At first it experiences no friction, but when it passes the red line, it experiences a constant kinetic friction due to the floor until it comes to rest. Kinetic friction simulation Click "View this program" on the top left corner to view the VPython code.
- Fluid Friction This is a VPython simulation of a block moving through a tank of liquid. The only force acting on it is the fluid friction force (for convenience, we can say that the block has the same density as the liquid, so its weight is perfectly balanced by its buoyancy). A graph below the simulation shows its velocity over time. It decays exponentially, as described in the mathematical model section. Fluid friction simulation Click "View this program" on the top left corner to view the VPython code.
Examples
In addition to the problems below, try the problems on the Static Friction and Kinetic Friction pages for additional practice.
1. (Simple)
A 100kg box lies at rest on a flat table. The coefficient of static friction between the box and the table is [math]\displaystyle{ \mu_{s} = {.25} }[/math] and the coefficient of kinetic friction between the box and the table is [math]\displaystyle{ {μ}_{k} = {.15} }[/math]. What is the magnitude of the horizontal force required to move the block?
Solution:
Since the block is at rest, the friction between the box and the table is static. The magnitude of the horizontal force required to move the box must exceed the maximum static friction force, [math]\displaystyle{ F_{s, max} }[/math].
[math]\displaystyle{ {F}_{s, max} = \mu_s * N }[/math]
[math]\displaystyle{ \mu_s }[/math] is given. The normal force between the block and the table can be found by reasoning that it is equal in magnitude to the weight of the block, or the block would be accelerating up or down. The normal force is therefore given by
[math]\displaystyle{ N = m * g }[/math]
[math]\displaystyle{ N = 100 * 9.8 }[/math] Newtons
[math]\displaystyle{ {F}_{s} = {.25}*{100}*{9.8} = {245} }[/math] Newtons
The force necessary to move the box must be at least 245 Newtons.
2. (Middling)
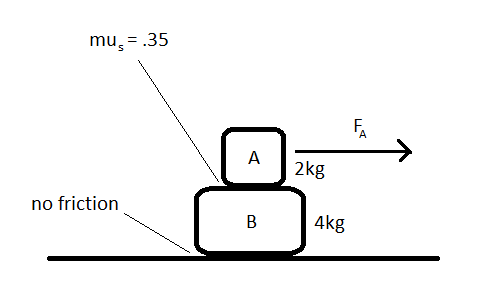
Two blocks are stacked on top of one another on a frictionless surface. The top block, block A, has a mass of 2kg, and the bottom block, block B, has a mass of 4kg. The coefficient of static friction between the blocks is [math]\displaystyle{ \mu_s = .35 }[/math]. A horizontal rightward force, [math]\displaystyle{ F_A }[/math], is applied to block A. Find the maximum magnitude of [math]\displaystyle{ F_A }[/math] that can be applied to Block A so that the blocks stay together.
Solution:
Let us consider the forces acting on each of the two boxes. Let us define the rightward direction as the positive direction.
Forces on Block A:
[math]\displaystyle{ F_A - F_s }[/math]
Forces on Block B:
[math]\displaystyle{ F_s }[/math]
Since we want the blocks to move together, they must have the same acceleration. Let us call this acceleration a.
By using Newton's second law, [math]\displaystyle{ \vec{f} = m \vec{a} }[/math], we can come up with an equation for block A and an equation for block B, creating a system of equations:
Block A:
[math]\displaystyle{ F_A - F_s = 2 a }[/math]
Block B:
[math]\displaystyle{ F_s = 4 a }[/math]
Dividing the second equation by 2 yields
[math]\displaystyle{ \frac{1}{2}F_s = 2 a }[/math]
Substituting this value for 2a into the first equation yields
[math]\displaystyle{ F_A - F_s = \frac{1}{2}F_s }[/math]
[math]\displaystyle{ F_A = \frac{3}{2}F_s }[/math]
This equation makes sense; a greater applied force would require more static friction in order to keep the two blocks together. Since we want to find the maximum value for [math]\displaystyle{ F_A }[/math], let us substitute the maximum value for [math]\displaystyle{ F_s }[/math]:
[math]\displaystyle{ F_A = \frac{3}{2}*\mu_s*N }[/math]
[math]\displaystyle{ F_A = \frac{3}{2}*.35*2*9.8 }[/math] (the normal force between the two blocks must equal the weight of the top block, which is [math]\displaystyle{ 2*9.8 }[/math], or the top block would accelerate vertically)
[math]\displaystyle{ F_A = 10.29 }[/math]N.
3. (Difficult)
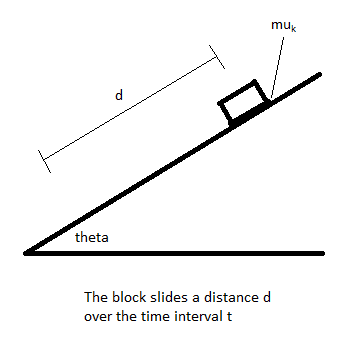
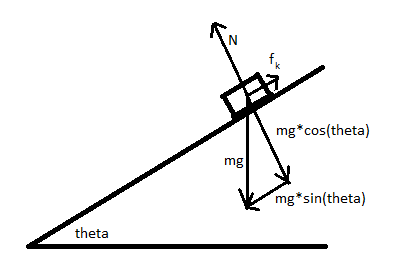
A block is released from rest on an inclined surface that makes angle [math]\displaystyle{ \theta }[/math] with the horizontal. The block takes an amount of time [math]\displaystyle{ t }[/math] to travel a diagonal distance [math]\displaystyle{ d }[/math] down the inclined surface. What is the coefficient of kinetic friction [math]\displaystyle{ \mu_k }[/math] between the block and the inclined surface?
Solution:
Since the normal force as well as the direction of the block's travel are constant, the kinetic friction force is constant too. Since the only forces acting on the block are gravity, the normal force, and kinetic friction, all of which are constant, the acceleration of the block must be constant. This allows us to use the following kinematic equation to solve for acceleration:
Let us say the block has mass [math]\displaystyle{ m }[/math]. Now we can use Newton's second law in the form [math]\displaystyle{ \vec{f}_{net} = m\vec{a} }[/math] to solve for the net force:
We know that F_{net} is the vector sum of gravity, the normal force, and the friction force. As with the traditional frictionless block-on-a-ramp problem, the component of gravity perpendicular to the inclined surface ([math]\displaystyle{ mg\cos\theta }[/math]) is balanced by the normal force, leaving the component of gravity parallel to the inclined surface ([math]\displaystyle{ mg\sin\theta }[/math]) pointing down along the ramp. However, there is now a third force we need to take into account: the friction force, which opposes the direction of the block's motion and therefore points up along the ramp.
Let us define the positive direction as down the ramp. This means the net force is given by
[math]\displaystyle{ F_{net} = mg\sin\theta - f_k }[/math].
Setting this equal to the expression for net force found earlier yields
4. (Difficult)
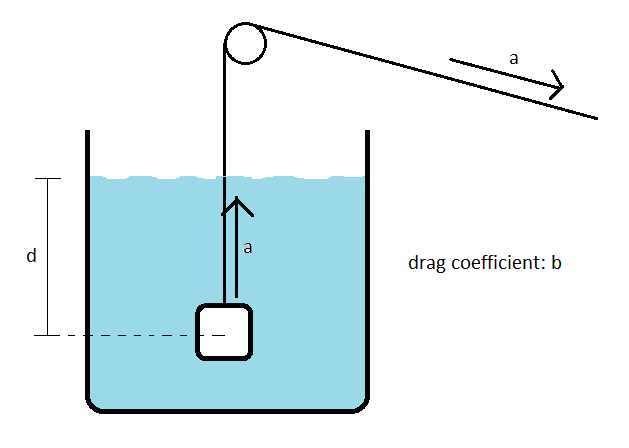
A block is suspended at rest in a tank of water, a distance [math]\displaystyle{ d }[/math] below the surface. It has the same density as water, so the gravitational force acting on it is cancelled by an upward buoyant force. A rope of negligible mass is connected to the block and is used to lift it up out of the tank. Due to the rope, the block accelerates upwards at a constant rate [math]\displaystyle{ a }[/math]. How much energy has been dissipated into the water as thermal energy as a result of fluid friction by the time the block emerges from the surface? The drag coefficient of the block in water is [math]\displaystyle{ b }[/math] and the rope has a negligible drag coefficient because of its slim profile.
Solution:
Fluid friction does negative work on the block. The absolute value of the work done by fluid friction is the amount of energy it dissipates into the environment as thermal energy. Let us find the work done by fluid friction on the block by integrating its force over the distance over which it is exerted:
The energy dissipated into the water as thermal energy as a result of fluid friction by the time the block emerges from the surface is [math]\displaystyle{ \frac{2}{3}b\sqrt{2a}d^\frac{3}{2} }[/math].
Connectedness
Friction has countless applications in industry and everyday life. In some scenarios, such as in engines and motors, it is undesirable, as it dissipates power that would otherwise be delivered to a useful task. In these cases, it is important to understand friction so that it can be minimized and factored into calculations. In other scenarios, such as on the brakes of a car, friction is desirable and necessary, and it is important to understand friction so that it can be maximized and calculated. In addition to affecting motion, kinetic friction raises temperatures, can wear down objects, and can emit sound, which may also need to be taken into account, depending on the application. There are many, many situations and technologies where friction plays a critical role. Here are a few examples.
Wheels
Sliding objects along the ground can be difficult. Enter one of the oldest inventions of mankind: the wheel. Wheels significantly reduce the power dissipated by kinetic friction by changing where it takes place, and, in doing so, changing the distance over which it is exerted. Consider a situation in which a person wants to push two boxes across the floor: one with wheels and one without. On the box without wheels, kinetic friction takes place between the floor and the bottom of the box. The friction force does negative work on the box equal to the product of its magnitude and the distance over which it was exerted, which is the distance traveled by the box. On the box with wheels, the friction at the point of contact between the wheels and the floor is static because the wheels roll rather than slide. This static friction force is not exerted over any distance, because the point of contact between the ground and each wheel changes rather than moves. It therefore does no work. Kinetic friction is still present; it now occurs between the wheels' axles and the brackets that hold them to the underside of the box. The axle rotates within its brackets, so sliding occurs. (Alternatively, if the axle is fixed and doesn't rotate, the kinetic friction occurs where each wheel slides around the axle that holds it.) The normal force between the brackets and the axle is the same as the normal force between the box without wheels and the floor; that is, the weight of the box. However, because the radius of the axle is significantly smaller than the radius of the wheel, this kinetic friction force is exerted over a much smaller distance. In other words, which each rotation an axle makes, the outer edge of the wheel travels much farther than the outer edge of the axle, so the distance over which the force is exerted is much smaller than the distance traveled by the box. This means that the negative work done on the box with wheels is smaller in magnitude than the negative work done on the sliding box. Another way of thinking about it is that the radius of the axle is so small that friction barely exerts any torque on it.
Driving and walking
Static friction between the car wheels and the ground is responsible for the car's acceleration. Without static friction, pressing the accelerator would simply cause the wheels to spin in place over the ground. Similarly, static friction between our feet and the ground allows us to walk by pushing off of the ground.
Swimming
Fluid friction allows us to swim. When a swimmer makes a stroke, they push back with cupped hands, which is a shape designed to have a high drag coefficient with the water. The resistance the hands encounter as they push back drives the swimmer forward.
Ball bearings
Ball bearings reduce friction between a rotating axle and the bracket or frame that holds it. A ball bearing consists of a rotating inner cylinder inside a hollow outer cylinder that holds it. The inner and outer cylinders do not touch but are separated by a layer of spheres that turn so that there is only static friction. In fact, in a theoretical ideal ball bearing, there is no kinetic friction and therefore no loss of energy. In real ball bearings, some slipping does occur between the balls and the cylinders, and the balls may come into contact with each other or the casing that holds them in place. Ball bearings are often used around the axles of wheels to make pushing carts easier, or in conjunction with motors in robots to reduce the wasting of energy.
Lubricants
Lubricants reduce friction between sliding surfaces. A lubricant is a fluid that separates two sliding surfaces. The result is that kinetic friction is replaced with fluid friction, usually with a low drag coefficient because only a surface is in contact with the fluid, in contrast to traditional fluid friction, where a submerged object is surrounded by the fluid and the fluid has to be displaced to allow the object to move). Lubricants may be used in engines to reduce abrasion and the wasting of power due to friction, or in other devices, such as squeaky door hinges, to reduce the sound emitted as a result of friction.
Screws, nails, and bolts
Screws, nails, and bolts fix objects together and rely on friction to do so. Screws and nails are inserted directly into a material. The fact that they have to displace that material in order to fit in compresses that material, which in turn causes a high normal force between the material and the sides of the nail or screw. This makes it difficult to pull it out, especially in the case of screws, where the twisting motion necessary increases the distance over which the friction force is exerted and therefore increases the energy required to remove it. A bolt similarly experiences a high normal force between its outer edge and the inner edge of the corresponding nut, which is manufactured to be a tight fit.
Machine belts
Machine belts transmit power from one spinning wheel to another in a variety of machines. Static friction between the belt and each wheel allows for this.
Holding objects
Friction is in part what allows us to hold objects in our hands. The normal force provided by our grip creates a static friction between the hand and the object.
Rubbing hands together for warmth
Rubbing our hands together for warmth is possible because of friction. The kinetic friction between our hands causes the kinetic energy of our hands to be converted into thermal energy. Our muscles continually supply a new source of kinetic energy. Similarly, sticks can be rubbed together to create enough heat for fire.
Sandpaper
The abrasive nature of friction is often undesirable, but for sandpaper, it is essential. Sandpaper uses kinetic friction to wear off the uneven protrusions on a surface to make it smoother. Belt sanders can even be used to remove large volumes of material, for example to round a sharp corner.
Removing a cork
To remove a cork stuck in the neck of a bottle, it is easier to pull out the cork while twisting it. This is because it is relatively easy to twist the cork if you have a large enough lever arm to exert a large torque. Once the cork is rotating, the force required to pull it out of the bottle is reduced because the friction between the cork and the bottle is now kinetic instead of static. This is because [math]\displaystyle{ \mu_k \lt \mu_s }[/math], and the normal force between the cork and the bottle is the same.
History
Evidence of human knowledge of friction is very old. Tools intended to start fires by friction have been dated to at least 50,000 BC, and wheels are estimated to have been invented in 8,000 BC in Asia. Ancient Egyptian art from about 2,000 BC depicts the use of lubricants under sledges used to transport large objects and in the axles of chariots. The Greek philosopher Themistius (390-320 BC) is widely considered the first individual to make an explicit observation about friction: he stated that static friction is greater than sliding (kinetic) friction. Leonardo Da Vinci (1452-1519) also studied friction. He observed that rougher materials experience more friction, that the friction force between two objects was proportional to the normal force between them, and that the friction force between two objects did not depend on their area of contact. Unfortunately, he made these observations in one of his many notebooks without publishing them, and no one recognized the notes' importance until after the observations had been independently rediscovered by Guillaume Amontons (1663-1705). Amontons published his discoveries in 1699. In addition to what had already been observed by Da Vinci, Amontons added that the kinetic friction force is independent of the sliding speed, and speculated about the causes of friction. Isaac Newton (1642-1727) was the first to describe fluid friction in his work titled Principia Mathematica in 1687. Charles-Augustin Coulomb (1736-1806) performed many experiments supporting earlier discoveries and stated that the friction experienced by a load on wheels is inversely proportional to the radius of the wheels. F. Philip Bowden and David Tabor wrote in 1950 that friction was largely the result of adhesive forces between surfaces. These adhesive forces were proportional to the number and size of contact points between the surfaces, which were in turn proportional to the normal force between them. This is believed to be the cause for friction today.
See also
- Static Friction
- Kinetic Friction
- Thermal Energy
- Air Resistance
- Terminal Velocity and Friction Due to Air
- Rolling Motion
External links
References
- Serway, Raymond A., and John W. Jewett. Physics for Scientists and Engineers. Boston, MA: Cengage Brooks/Cole, 2014. Print.
- Sherwood, Bruce A. Matter & Interactions. By Ruth W. Chabay. 4th ed. Vol. 1. N.p.: John Wiley & Sons, 2015. 45-50. Print. Modern Mechanics.
- http://www.tribonet.org/tribology-history/
- http://www.tribology-abc.com/abc/history.htm
- https://en.wikipedia.org/wiki/Friction#History
- https://books.google.com/books?id=0-xOM8y6Uc8C&pg=PA27&lpg=PA27&dq=Themistius+friction&source=bl&ots=9x8tdU-XAY&sig=ACfU3U1knqirFiH8A9xc2kJc6Zbi2vGa8Q&hl=en&sa=X&ved=2ahUKEwjttOnQ2JvjAhXjYt8KHcZXDgwQ6AEwEHoECAgQAQ#v=onepage&q=Themistius%20friction&f=false