SI Units
This page describes the International System of Units and lists its units.
Recently Edited by DAVID SHIN
The Main Idea
The International System of Units is a set of units allowing for the quantification of each physical dimension. It was invented in France as an extension of the metric system under the name "Système Internationale d'Unités," which is why it is abbreviated to "SI". SI Units are practically universally used for scientific applications, and are used in most countries in everyday life as well, although the United States, which uses customary units, is a notable exception. Most of quantities in this course will be given in SI units.
The International System of Units has seven base units with specific definitions and countless derived units which are created by multiplying and dividing the base units. For example, the meter (m) is the base unit for the dimension distance and the second (s) is the base unit for the dimension time. The meter per second (m/s) measures the dimension speed and is a derived unit because it can be obtained by dividing the meter by the second.
Because measurements must often be made on many different scales, the International System of Units also defines a variety of prefixes for use with its units. The prefixes scale the values of each unit by powers of 10.
The International System of Units is adaptable and can change over time to meet the evolving needs of scientists. Over the last several centuries, the number of base units has grown from 3 to 7 as a result of the discovery of new dimensions that could not be expressed in terms of existing base units. The number of derived units recognized as meaningful has also grown substantially and will likely continue to as the human understanding of the physical world improves. Additionally, the seven base units have undergone redefinition at several points in time, most recently on May 20 2019. The purpose of each redefinition is not to change the units' values (in fact, their values are changed as little as possible), but to make their definitions more universally constant and reproducible.
SI units are important because they provide a consistent, universally accepted framework for making and comparing measurements, which is essential for clear communication in science, engineering, and everyday life. By ensuring that all researchers and professionals use the same standardized units, the SI system eliminates confusion, reduces errors, and allows experiments and calculations to be replicated anywhere in the world - providing a strong translational framework for computational work. This consistency is especially crucial in global collaboration, manufacturing, medicine, and technology, where even small discrepancies in units can lead to major mistakes. Their adaptability and precision make SI units the foundation upon which modern scientific understanding continues to grow.
The Seven Base Units
The values of the seven base units are historically motivated, but most of their current definitions have been changed from the original. Today, each of the 7 base unit is defined by fixing a specific natural universal constant at a certain numerical value.
Second (s)
The second measures time.
Today, the second is defined by fixing the value of the cesium hyperfine transition frequency [math]\displaystyle{ \Delta v_{Cs} }[/math] at exactly 9192631770 hz (transitions per second). This defines the second as the 9192631770 times the period of the transition between the two levels of the ground state of cesium-133 atom. Atomic clocks make use of this phenomenon by counting the cesium transitions as a mechanism for keeping time! This definition was instated in 1967.
The second was initially defined as a fraction (1/86400) of a day of 24 hours of 60 minutes of 60 seconds. This definition is poor primarily because the duration of the day changes slightly over time. In 1956 the second was defined as 1/31556925.9747 of the tropical year. (The tropical year is the time it takes the sun to return to the same position in the season cycle, which is about 20 minutes shorter than the causal year.) However, this is still not as elegant as the current definition because it is based on our particular solar system, which may not always exist or be available for measuring.
Meter (m)
The meter measures distance.
Today, the meter is defined by fixing the value of the speed of light in a vacuum [math]\displaystyle{ c }[/math] at exactly 299,792,458 m/s. Since the second is already defined, this defines the meter as the distance traveled by light in a vacuum in 1/29979248th of a second.
The meter was originally defined in 1973 as 1/10,000,000 of the meridian through Paris between the North Pole and the Equator. In 1960 it was redefined as 1650763.73 wavelengths of the radiation in a vacuum corresponding to the transition between 2p10 and 5d5 transition levels of the krypton-86 atom.
Kilogram (kg)
The kilogram measures mass.
Today, the kilogram is defined by fixing the value of Planck's constant [math]\displaystyle{ h }[/math] at exactly 6.62607015×10−34 J s. Recall that the joule is not a base unit, but a derived unit equal to the kg m2/s2. Since the meter and the second are already defined, this leaves only one possible value for the kilogram. This definition was instated as part of the SI unit redefinition of May 20, 2019. This video by the science YouTube channel Veritasium describes the redefinition of base units of May 20, 2019, with an emphasis on the new definition of the kilogram.
In 1973, the SI unit for mass was called the grave. It was defined as being the mass of 1 liter of pure water at its freezing temperature. The grave was renamed to the kilogram, and later, in 1889, it was redefined as the mass of a specific sample of a platinum alloy. The sample is called "Le Grand K" and is kept in a humidity-controlled vault just outside of Paris, France. This definition was inadequate because it was not universally reproducible, so they considered a few alternate definitions, and, in 2019, redefined it to the current definition. This video from 2013, also by Veritasium, explains the shortcomings of Le Grand K and describes a proposed alternate definition that was being considered at that time (although it did not end up being the chosen definition).
Ampere (A)
The ampere measures electrical current.
Today the ampere is defined by fixing the value of the elementary charge [math]\displaystyle{ e }[/math] at exactly 1.602176634e-19 C. This defines the Coulomb, and since an ampere is 1 Coulomb per second (and the second is already defined), it also defines the Ampere.
In 1881, the ampere was defined as a tenth of the current required to create a magnetic field of one Oersted at the center of a 1cm arc of wire with curve radius 1cm. In 1946, the ampere was defined as the current required to create a force of 2e-7 Newtons per meter of length between two straight parallel conductors of infinite length placed 1m apart in a vacuum. This video by the physics YouTube channel Kaustubhan describes the 1946 definition of the Ampere.
Kelvin (K)
The Kelvin measures temperature.
Today, the Kelvin is defined by fixing the value of the Boltzmann constant [math]\displaystyle{ k }[/math] at exactly 1.380649 x 10–23 J/K. Since the joule is a derived unit derived from the second, the meter, and the kilogram, each of which has already been defined, this leaves only one possible value for the Kelvin.
Mole (mol)
The mole measures the amount of a substance present by number of particles.
Today, the mole is defined by fixing the value of the Avogadro constant [math]\displaystyle{ N_A }[/math] at exactly 6.022140857 × 1023 mol-1. This defines the mol to be 6.022140857 × 1023 mol particles.
The mol was originally defined in 1967 the mole as the number of carbon-12 atoms necessary to comprise a 12 gram sample.
Candela (cd)
The candela measures luminous intensity.
Today, the candela is defined by fixing the value of the luminous efficacy constant [math]\displaystyle{ K_{cd} }[/math] at exactly 683 lumens per watt. This defines the candela as the luminous instensity of a source that emits radiation of a frequency 5.4e14 Hz in 1/683 of a steradian. (A steradian is the 3D analog for the radian; it is a part of the sphere's surface area equalling the radius squared in area.) This is about the luminous intensity of a candle.
Derived Units
There are many useful quantities in physics that cannot be measured in a single base unit. These must be expressed in derived units, which are obtained by multiplying and dividing the base units. For example, the meter (m) is the base unit for the dimension distance and the second (s) is the base unit for the dimension time. The meter per second (m/s) measures the dimension speed and is a derived unit because it can be obtained by dividing the meter by the second. Speed does not get its own base unit because it does not need one; speed is fundamentally a relationship between distance and time (specifically, distance traveled and the time it takes to travel that distance). Other examples of derived SI units are the kg/m3, which measures density, and the kgm/s, which measures momentum.
Some derived units are used so frequently in physics that they are given their own names. Below are several such derived units:
| Unit | Symbol | In Terms of Base Units | Dimension |
|---|---|---|---|
| hertz | Hz | [math]\displaystyle{ \mathrm{s}^{-1} }[/math] | frequency |
| newton | N | [math]\displaystyle{ \frac{\mathrm{kg}\mathrm{m}}{\mathrm{s}^2} }[/math] | force |
| pascal | Pa | [math]\displaystyle{ \frac{\mathrm{kg}}{\mathrm{m}\mathrm{s}^2} }[/math] | pressure |
| joule | J | [math]\displaystyle{ \frac{\mathrm{kg}\mathrm{m}^2}{\mathrm{s}^2} }[/math] | energy |
| watt | W | [math]\displaystyle{ \frac{\mathrm{kg}\mathrm{m}^2}{\mathrm{s}^3} }[/math] | power |
| coulomb | C | [math]\displaystyle{ \mathrm{As} }[/math] | charge |
| volt | V | [math]\displaystyle{ \frac{\mathrm{kg}\mathrm{m}^2}{\mathrm{A}\mathrm{s}^3} }[/math] | electric potential |
This list is not comprehensive, and there are many unnamed derived units that are commonly used as well.
Prefixes
Because measurements must often be made on many different scales, the International System of Units also defines a variety of prefixes for use with its units. The prefixes scale the values of each unit by powers of 10. For example, the kilometer is 1000 times as long as the meter because of the prefix "kilo." The use of prefixes allows even large and small measurements to be reported with reasonable and easy to read numbers. For example, it is easier to express the atomic radius of the hydrogen atom as 53 picometers than 5.3 x 10-11 meters.
Each prefix has a symbol, which can be combined with the symbol of a unit. For example, the symbol for pico is "p", so "pm" is the symbol for picometer.
The following table shows the common prefixes used with SI units.
| Prefix | Symbol | Multiplier |
|---|---|---|
| peta | P | 1015 |
| tera | T | 1012 |
| giga | G | 109 |
| mega | M | 106 |
| kilo | k | 1000 (103) |
| hecto | h | 100 (102) |
| deka | da | 10 (101) |
| deci | d | .1 (10-1) |
| centi | c | .01 (10-2) |
| milli | m | .001 (10-3) |
| micro | [math]\displaystyle{ \mu }[/math] | 10-6 |
| nano | n | 10-9 |
| pico | p | 10-12 |
| femto | f | 10-15 |
There are several popular mnemonic devices for remembering some of the prefixes. A common example is "King Henry Died by Drinking Chocolate Milk." The first letter of each word represents a prefix, starting at kilo and ending at mili. The "b" in "by" stands for "base unit," which in this context means a unit with no prefixes.
Dimensional Analysis
Dimensional analysis is the analysis of the units used in expressions and equations. Dimensional analysis revolves around the fact that when two quantities, each measured with a specific unit, are multiplied or divided, their units are multiplied or divided as well. For example, consider car traveling in a straight line at a constant speed of 20m/s. Suppose you want to know how far it travels in 30 seconds. To calculate the answer, simply multiply 20m/s by 30s, which is 600m. Notice that the meter per second times the second equals the meter.
A result of the above rule is the fact that both sides of an equation must have the same units. This makes sense because two quantities in different dimensions can't be compared. To illustrate this fact, consider the ideal gas law:
[math]\displaystyle{ PV=nRT }[/math]
where [math]\displaystyle{ P }[/math] is the pressure of the gas, [math]\displaystyle{ V }[/math] is its volume, [math]\displaystyle{ n }[/math] is the number moles of the gas, [math]\displaystyle{ R }[/math] is the ideal gas constant, and [math]\displaystyle{ T }[/math] is the temperature of the gas.
For the ideal gas law to be numerically true, the ideal gas constant [math]\displaystyle{ R }[/math] must be in the correct units. The SI units for pressure, volume, and temperature respectively are the kilopascal (kPa), the cubic meter (m3), and Kelvin (K). If these units are used, [math]\displaystyle{ R }[/math] must be given in m3 kPa / mol K. That way, both sides of the equation are in m3 kPa. R can also be given in other units, as long as they are a unit of volume times a unit of pressure divided by moles and a unit of temperature. Its value depends on the units used. In fact, all natural constants can have different values depending on the units in which they are given. In this class, they are typically given in their SI units.
All equations in physics, like [math]\displaystyle{ PV=nRT }[/math], are true for all units, as long as their two sides agree in units, which requires the correct versions of any natural constants. Generally, SI units are preferred. For example, the general force equation [math]\displaystyle{ F = ma }[/math] and the force gravity equation [math]\displaystyle{ F = mg }[/math] display that both sides equal Newtons, or kg(m/s^2) which are the units of m and a/g respectively.
The fact that both sides of an equation must have the same units can be useful for determining the units of a quantity, or, if the units of all quantities are known, for verifying that a derived equation makes sense and is possible.
Unit Conversion
Measured quantities can be converted from one unit to another as long as the relationship between the two units is known. To do so, the quantity should be multiplied by the ratio of the two units' values, with the quantity's current unit in the denominator and the target unit in the numerator. This ratio is called a conversion factor. For example, suppose you want to convert 7cm to inches, given that an inch is equivalent to 2.54cm. 7cm should be multiplied by the ratio of the inch to the centimeter, which is [math]\displaystyle{ \frac{1\mathrm{in}}{2.54\mathrm{cm}} }[/math]:
[math]\displaystyle{ 7\mathrm{cm} * \frac{1\mathrm{in}}{2.54\mathrm{cm}} = 2.76\mathrm{in} }[/math].
It is also possible to use this method to convert between units that measure different dimensions, as long as they are proportional to each other and the relationship between them is known. For example, it is possible to convert from the volume of a sample of a substance to its mass if its density is known:
[math]\displaystyle{ .125\mathrm{m}^3\mathrm{ steel} * \frac{8050\mathrm{kg steel}}{1 \mathrm{m}^3\mathrm{ steel}} = 1006.25\mathrm{kg steel} }[/math]
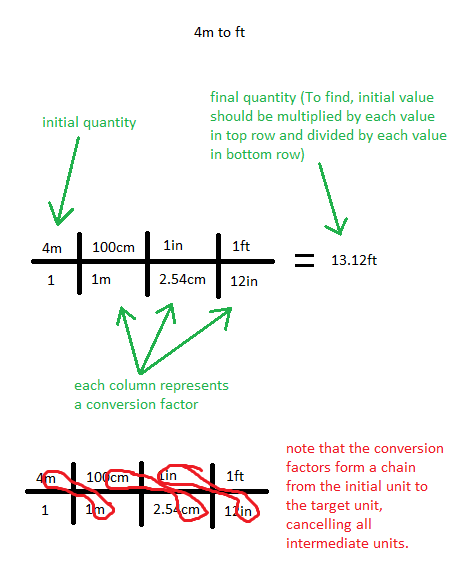
Sometimes, it is necessary to perform many conversions in sequence. For example, consider a person who wants to convert from meters to feet, but the only relationship they know between SI and customary length units is that an inch is equivalent to 2.54cm. They would first have to convert meters to centimeters, then centimeters to inches, then inches to feet. In such a situation, it is often helpful to use a notation such as the one below to keep track of the conversions:
Each column represents the conversion from one unit to another using a different conversion factor. Each unit in the top (except the target unit) should cancel with a different unit in the bottom.
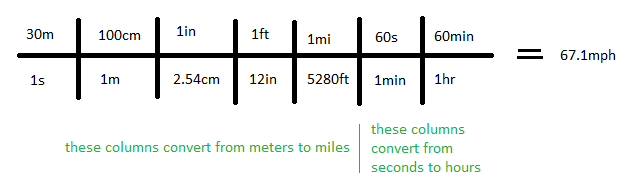
It is also possible to convert between complex units with both a numerator and a denominator. The following chart converts from meters per second to miles per hour. Some columns are for converting from meters to miles and others are for converting from seconds to hours.
Finally, it is worth noting that when converting between higher powers of units, such as cubic inches to cubic cm, their conversion factors are raised to that power also. That is, one inch is equivalent to 2.54 cm, so one cubic inch is equivalent to 2.543 = 16.39 cubic cm.
Below is an example of dimensional analysis within Glowscript to convert from inches to meters. You divide inches by 12 and 3.281 as there are 12 inches per foot, and 3.281 feet per meter.
https://www.glowscript.org/#/user/david.shin/folder/MyPrograms/program/webpage/edit
Examples
Simple
The law of universal gravitation states that the magnitude of the gravitational force between two objects of masses [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2 }[/math] is given by
[math]\displaystyle{ |\vec{F}_{grav}| = \frac{Gm_1m_2}{r^2} }[/math],
where [math]\displaystyle{ G }[/math] is the universal gravitational force constant and [math]\displaystyle{ r }[/math] is the distance between the objects' centers of mass.
Assuming that [math]\displaystyle{ |\vec{F}_{grav}| }[/math], [math]\displaystyle{ m_1 }[/math], [math]\displaystyle{ m_2 }[/math], and [math]\displaystyle{ r }[/math] are given in their respective standard SI units, what units should G have?
Solution:
The left side of the equation is in N because that is the SI unit for force. The right side of the equation must therefore also be in N. Ignoring the G, the right side of the equation has units of kg2/m2. G must introduce the unit N in the numerator while canceling the kg2/m2, so G has units of N*m2/kg2. This is equivalent to m3/kgs2 because 1N = 1kgm/s2. These two answers can also be written respectively as N*m2*kg-2 and m3*kg-1*s-2. Any of the 4 answers is correct.
Middling
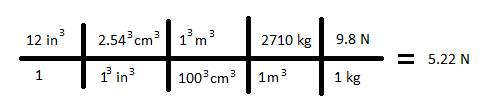
A rectangular prism made out of aluminum (density: 2,710kg/m3) has sides of length 1in, 2in, and 6in. 1 inch is equivalent to 2.54cm. What is the weight of the sample near the surface of the earth?
Solution:
The rectangular prism has a volume of 1in x 2in x 6in = 12in3. Let us use the unit conversion notation discussed earlier in the page to convert this volume to force:
Note that although g is normally thought of as having as units m/s2, we used it above as having units N/kg. These units make more sense when it serves as a constant of proportionality between weight (measured in N) and mass (measured in kg). These units are equivalent to m/s2.
Difficult
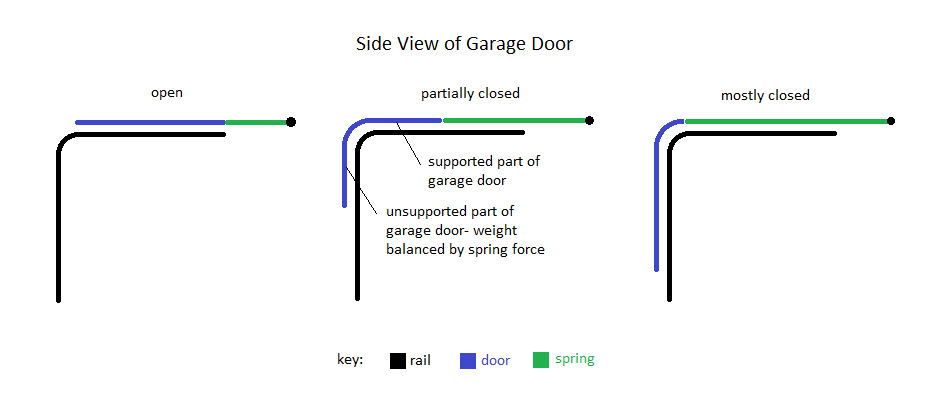
A garage door has a width of 2.5m, a width of 2.2m, and a thickness of 4cm. The average density of the materials that comprise it is 273 kg/m3.
The garage works like most home garages; it can slide up and down along a rail to open and close respectively, and the rail has a 90[math]\displaystyle{ ^\circ }[/math] turn (of small radius) in it so that when the garage door is closed, it is vertical, but when it is open, it hangs horizontally below the ceiling. When the garage is partially opened, the horizontal part of it is supported by the rail while the vertical part hangs freely. Because the garage door is intended to move at a constant speed, it is fitted with a spring designed to cancel the weight of the vertical part of the garage door regardless of the door's position. This makes it easier for the cable system to move the garage door. The spring obeys Hooke's Law. It is at its equilibrium length when the garage door is open and entirely supported by the rail, and as the garage door closes and more of its weight becomes unsupported, the spring extends to apply a force equal to the unsupported weight in the opposite direction.
What should be the spring constant k of the spring?
Solution:
Let d be the length of the vertical part of the garage door, in m. The volume of the vertical part of the garage door is 2.5 x .04 x d m3 = .1d m3. Its mass is .1d m3 x 273 kg/m3 = 27.3d kg. Its weight is 27.3d kg x 9.8 N/kg = 268d N. The displacement of the spring from its equilibrium length is also d due to the geometry of the garage door system. According to Hooke's Law, the spring must exert a force whose magnitude is given by f = kd, where k is the spring constant of the spring. The magnitude of the force of the spring must equal the weight of the vertical part of the garage door, which is 268d Newtons, so k must equal 268 N/m.
Connectedness
Physics can be thought of as the study of quantifying natural phenomena, which could not be done without some system of units allowing for measurements and calculations to be made. The SI unit system is a good candidate for a number of reasons: its units can apply to quantities on many different scales, new and existing units can be defined and redefined as necessary, and each unit is defined in such a way that they can be replicated with high precision by anyone at any place and time, provided they have the resources to perform certain experiments. The SI system is connected to all of physics (and, indeed, all of science) because practically the entire scientific community has agreed to use it for all measurements and calculations. A basic understanding of the SI system is necessary for any type of technical industry (engineering, architecture, etc.) in most countries outside the united states, where the SI system is used for such industries (the United States uses the customary system for all industries except pure science). An in-depth understanding of the SI system is necessary for certain industries with very small tolerances, such as the creation of precision machine tools.
History
The Metric System was created around the time of the French Revolution. On June 22, 1799, two platinum standards defining the meter and the kilogram were deposited in the Archives de la Republic in Paris. This can be seen as the first step in the development of the present International System of Units. The values of the meter and the kg were based on the physical world; the meter was based on the dimensions of the earth and the kilogram was based on the density of water. These two units formed the foundation of what was then called the metric system. The metric system was abandoned and then readopted by France, and slowly gained popularity in the scientific communities of other countries. James Maxwell proposed the addition of the second as a third base unit for time, which was quickly instated, and Giovanni Giorgi, an Italian physicist and electrical engineer, advocated for the addition of a fourth base unit to describe electromagnetic phenomena. The ampere was defined in 1935 for this purpose. By the 20th century, the metric system was commonplace across scientific communities across the world.
The SI unit system was established in 1960 by the 11th General Conference on Weights and Measures (CGPM), a part of the International Bureau of Weights and Measures (BIPM). The CGPM is an international authority on units recognized by most scientists which aims to standardized the units used around the world. The SI system adopted the four base units of the metric system and added three additional base units: the Kelvin, the candela, and the mole. Since then, the CGPM has continued to occasionally redefine the base SI units.
See Also
Further reading
SI Units for Clinical Measurement 1st Edition by Donald S. Young
External Links
https://www.youtube.com/watch?v=c_e1wITe_ig&t=521s (Video describing the redefinition of SI base units of May 20 2019)
http://wps.prenhall.com/wps/media/objects/165/169061/blb9ch0104.html (Pearson educational site)
http://physics.nist.gov/ (National institute of standards and Technology)
https://www.bipm.org/en/measurement-units/ (International Bureau of Weights and Measures site)
References
Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)
Tutorial & Drill Problems for General Chemistry (and Intro) By Walter S. Hamilton, Ph.D.
Base units of the SI, fundamental constants and modern quantum physics By Christian J Bordé, Published 15 September 2005