Point Particle Systems: Difference between revisions

From Physics Book
Jump to navigation Jump to search
 
(109 intermediate revisions by the same user not shown)
Line 1: Line 1:
This page describes the model in which systems are represented as point particles.
This page describes point particle systems and how they can be used to model certain aspects of a system's motion.


==The Main Idea==
==The Main Idea==


A point particle system is a physical system in which each multidimensional rigid body of matter is modeled as a particle that exists at a single point in space. In such a model, a point somewhere on the body is chosen to represent the entire body. Often, this point is its center of mass. The geometry of the body, including the spatial distribution of its mass, is ignored; all of the body's mass is considered to exist at the chosen representative point. Point particle systems are in contrast to [[Real Systems]], which respect the geometry of bodies of matter.
A point particle system is a physical system, usually composed of multiple parts, modeled as though it were a single particle at its [[Center of Mass]].


Point particle systems are used to represent certain types of systems because they simplify some of the math involved in analyzing their motion. That said, only certain aspects of a system's motion can be accurately modeled if it is treated as a point mass system. For example, a particle's translational [[Acceleration]] can be accurately found using the forces acting on the particle along with the particle's mass. However, the rotation of an object cannot be modeled if it is treated as a single point. This is because it is meaningless to describe a point as "rotating" since it has no geometry. The mathematical model section describes in more detail what point particle systems can and cannot model.
When work is done on a system, the energy imparted on it may take on multiple forms. These include [[Translational, Rotational and Vibrational Energy]], [[Potential Energy]], and [[Thermal Energy]]. Translational kinetic energy is kinetic energy due to the movement of the system's center of mass. All other types of energy the system has are considered "internal" types of energy because they do not affect the system's motion through its environment, but rather indicate its local properties. Sometimes, when work is done on a system, it imparts both translational kinetic energy and internal types of energy. For example, consider a ball rolling down a ramp. Gravity does work on the ball and increases its energy. It gains some translational kinetic energy (its center of mass gains a velocity down the ramp) and some rotational kinetic energy (its rolling motion causes it to rotate about its center of mass).


Although you may not have been aware of it, you have been modeling systems as point particle systems for most of the problems in this course so far. For example, consider a problem where a ball is thrown from a known position with a known initial velocity, and you are asked to find quantities such as the highest point in its trajectory and the horizontal distance it has traveled when it hits the ground. You would perform calculations as though the ball has a single position vector at any point in time, even though it is actually a 3D object that takes up a volume. In reality, you are modeling the behavior of a specific point on the ball, such as its center of mass, its topmost point, or its bottommost point. Usually, however, you don't even need to specify which point on the ball it is that you are using to represent it, especially when the problem itself treats it like a single point (like this one does). It is acceptable to treat the thrown ball as a point particle because the diameter of the ball is much smaller than the distances involved in its trajectory and because the problem is not concerned with the rotation of the ball.
Forces acting on a real system can affect both the system's translational acceleration and, depending what part of the system they act on, the internal state of the system. The purpose of modeling a system as a point particle system is to easier to calculate how forces acting on it affect its <i>translational</i> motion through its environment. By modeling the system as a point particle, all forces are assumed to act directly on the system’s center of mass, allowing us to examine only the translational effects of the forces. The net force acting on the point particle causes it to accelerate according to [[Newton's Second Law: the Momentum Principle]].
 
From an energy perspective, a real system might have multiple types of work done on it at once; it might experience an increase in translational kinetic energy as well as an increase in some types of internal energy. By modeling the system as a point particle, we find only some of the work that is actually done on the system because we look at the displacement of the system's center of mass rather than the part of the system on which the force acts. Specifically, we find the work that affects only its <i>translational</i> kinetic energy because translational kinetic energy is the only energy a system can have when it is reduced to a point particle.
 
Modeling a system as a point particle offers no insights about the internal state of the system because only forces and work affecting its translational motion can be found.
 
Point particle systems are in contrast to [[Real Systems]] (also known as extended systems), which analyze each part of a system individually instead of reducing it to a single point. Real systems can model a system's internal behavior in addition to its motion through its environment, although they can be very complicated and difficult to analyze quantitatively. Often, to obtain a complete model of a system's behavior, both point-particle and extended models are used.
 
You may not be aware of it, but you have been modeling systems as point particles for most problems through week 9 because you have mostly been analyzing the translational motion of rigid bodies without regard for their internal energies. Now that we are starting to look at internal types of energy, it becomes more important to separate point particle systems and real systems, and to understand what each model is able to accurately represent.


===A Mathematical Model===
===A Mathematical Model===


====What aspects of a system's motion can be accurately calculated if it is reduced to a point particle?====
The mathematical concepts used to analyze point particle systems depend on the system. Often, the [[Work/Energy|work-energy theorem]] is used. This section explains how to use the work-energy theorem for a point particle system because this is the concept that varies the most significantly from its application to real systems.
 
The work done on a point particle system is defined as
 
<math>W = \int \vec{F_{net}} \cdot d \vec{r}</math>,
 
where <math>\vec{r}</math> is the position of the particle.
 
Let us assume that the net force acting on the particle is constant, so that we can get rid of the integral, and that the net force acts in the direction of the particle's motion, so that we can replace the dot product with regular multiplication. This will be the case for most point particle system problems involving work. With these assumptions, the work done on a point particle is given by
 
<math> W = F_{net} * d </math>
 
where <math>F_{net}</math> is the magnitude of the net force acting on the particle and <math>d</math> is the distance over which the force is exerted. For point particle systems, that is the distance traveled by the particle. This contrasts with real systems, where the distance over which the force is exerted depends on the movement of particular parts within the system.


If an object is modeled as a point particle, the forces acting on it can be used along with the particle's mass to accurately find its the translational [[Acceleration]] (<math>\vec{a} = \frac{\vec{F}_{net}}{m}</math>). This is because the geometry of the object doesn't affect its acceleration; it doesn't matter what part of the object the forces act on for the purpose of finding acceleration. This acceleration can be correctly used with kinematic equations to model the particle's motion.
The work-energy theorem states that work done on a system increases that system's energy. A point particle cannot experience an increase in internal energy. For example, the moment of inertia of a point particle about its center of mass is 0, so it can have no rotational kinetic energy. This means that all of the work done on a point particle system becomes translational kinetic energy.


The [[Linear Momentum]] (<math>\vec{p} = m \vec{v}</math>) and translational [[Kinetic Energy]] (<math>KE = \frac{1}{2} m v^2</math>) an object can also be correctly calculated if the object is represented as a single point; the formulas simply use the mass and velocity of that point.
In other words, for a point particle system,


Finally, the [[Potential Energy]] of an object, which is a function of its position, can usually be found with little to no error if the object is treated as a point particle. Some common types of potential energy include gravitational potential energy near the surface of the earth, universal gravitational potential energy, and elastic potential energy. In situations where the potential energy function is nonlinear, such as in universal gravitational potential energy, the point on the object chosen to represent it may need to be a specific point to produce completely accurate results, but this is usually not an issue because you don't usually need to indicate which point you choose. Even if the wrong point is used, it usually introduces negligible error.
<math> \Delta KE = F_{net} * d </math>


One major aspect of an object's motion that can NOT be accurately modeled if it is reduced to a point particle is its rotation. Firstly, it is meaningless to describe a point as "rotating" because a point has no geometry. Secondly, if all of an object's mass is concentrated at a single point, that point becomes its center of mass, and its moment of inertia about that center of mass is 0. Thirdly, any forces acting on a point particle cannot possibly exert a torque on it because a point particle has no lever arm. As a result, a point particle can have no angular velocity, angular momentum, or rotational kinetic energy. This is fine if we are not interested in the object's rotational behavior, and the object's rotational behavior does not affect what we <b>are</b> interested in, such as in the above example of the thrown ball. However, in any case where the rotational behavior of the object is (or affects) the behavior of interest, the object must be modeled as a real system.
and


===A Computational Model===
<math> KE = \frac{1}{2} m v^2 </math>.


Most computer models of moving objects treat them as point particle systems. Consider [https://www.glowscript.org/#/user/YorickAndeweg/folder/PhysicsBookFolder/program/IterativePrediction1 this simulation of a thrown ball]. Click "view this program" in the top left corner. In vPython, each shape is displayed as a 3D object centered on its position vector, so the ball is assigned a radius for display purposes. However, for most of the computational parts of the simulation, the ball is treated as a single point; it only has one position vector, forces are not localized to specific parts of the ball, and its rotation is not tracked. However, there is one part of the simulation that recognizes that the ball is more than a point: the loop control header. The header is written so that the loop terminates when the position of the ball is within one ball-radius of the ground, as opposed to when the position vector itself is at the ground. This recognizes that the ball occupies space and that the bottommost point hits the ground before the center of mass does. In conclusion, computer models typically do use point particle systems, although they may recognize that objects take up space where necessary.
The two equations above are the basis for answering work/energy questions using point particle systems. It is important to remember that when modeling a system as a point particle system, calculating the work done on the system as described above does not find <b>all</b> of the work done on the system, but rather just the work that becomes translational kinetic energy.


==Examples==
==Examples==


For each of the following, determine whether a point particle system could be used to simplify the problem. If i
<!--HTML comment: if you are editing this section, please be aware that the page "Real Systems" refers to these examples.-->
 
===1. (Simple)===
 
A 60kg person jumps straight up in the air from a crouching position. From the time the person begins to push off of the ground to the time their feet leave the ground, their center of mass moves up 2m, and the normal force between the ground and the person's feet has a constant magnitude of twice the person's weight. Find the velocity of the jumper at the moment their feet leave the ground. Use 10m/s<sup>2</sup> for g.
 
Solution:
 
Let us model the person as a point particle system. A force diagram for the person would look like this:
 
[[File:Pointparticlesystemsforcediagram.png]]
 
The net force acting on the person is the vector sum of the upward normal force and the downward gravitational force, which is a 600N force upwards. This force is constant and in the same direction as the person's motion, so multiplying it by the 2m displacement of the center of mass yields the work done on the person by their muscles:


===1. Middling===
<math>W = 600 * 2 = 1200</math>Nm.


Consider a block of mass <math>m</math> placed on a ramp inclined to angle <math>\Theta</math>. The coefficient of kinetic friction between the block and
The person begins at rest, so their initial kinetic energy is 0J and their final energy is 1200J.


===2. Middling===
<math>\frac{1}{2} m v^2 = KE</math>


==Connectedness==
<math>\frac{1}{2} * 60 * v^2 = 1200</math>
#How is this topic connected to something that you are interested in?
 
<math> v = \sqrt{40} </math>m/s.
 
===2. (Middling)===
 
A giant 20kg yo-yo floats at rest in space. Its string (whose mass is negligible compared to the mass of the yo-yo) is pulled with a constant force of 8N. What is the speed of the yo-yo when it has travelled 5m?
 
[[File:Pointparticlesystemsyoyo.png]]
 
Solution:
 
Solving this problem using energy while treating the system as a real system would be difficult; it would require knowledge of rotational physics and would require more steps. Let us therefore analyze it as a point particle system. This allows us to find only the work done on the yo-yo that is converted to translational kinetic energy.
 
Treating the yo-yo as a point particle, the work done on it is given by the magnitude of the net force times the particle's displacement:
 
<math>W = 8 * 5 = 40</math>Nm
 
The point particle's kinetic energy was originally 0, so it is now 40J.
 
<math>KE = \frac{1}{2} m v^2</math>
 
<math>40 = \frac{1}{2} * 20 * v^2</math>
 
<math>v = 2</math>m/s.
 
The point particle represents the center of mass of the yo-yo, so it must be moving at 2m/s.
 
===3. (Middling)===
 
A 50kg metal sphere is suspended in the inside of a large cubic box of negligible mass by six rubber bands- one attaching the sphere to each face of the box. The box and the sphere are initially at rest. A 200N rightward force is applied to the side of the box, causing it to accelerate. At time <math>t_1</math>, the box has been displaced by 10m to the right. At this time, the sphere is no longer exactly in the center of the box; it is 1m to the left of the center of the box due to its inertia. What is the speed of the sphere at time <math>t_1</math>?
 
[[File:Pointparticlesystemspherebox.png]]
 
Solution:
 
Let us model the sphere-box system as a point particle system. The center of mass of the system is simply the center of the sphere because the box has negligible mass. The work done on the particle is given by the force acting on the particle times its displacement:
 
<math>W = 200 * 9 = 1800</math>Nm. The displacement of the particle is only 9m because although the box was displaced 10m, the sphere was only displaced 9m due to its inertia and the non-rigidity of its suspension within the box.
 
The particle initially had no energy, so its energy at time <math>t_1</math> is 1800J.
 
<math>KE = \frac{1}{2} m v^2</math>
 
<math>1800 = \frac{1}{2} * 50 * v^2</math>
 
<math>v = \sqrt{72}</math>m/s.
 
===4. (Middling)===
 
A uniform disk of mass <math>M</math> starts at rest and rolls without slipping down a ramp. The plane of the ramp makes an angle of <Math>\Theta</Math> with the horizontal. The force of [[Static Friction]] acting on the bottom of such a disk, causing it to rotate, always has a magnitude of 1/3 the force acting to move the disk down the ramp. What is the translational speed of the disk after it has traveled a distance of <math>d</math> diagonally down the ramp?
 
[[File:Pointparticlesystemsramp.png]]
 
Solution:
 
Let us analyze this system as a point particle system because we are only interested in its translational motion.
 
The component of the disk's weight perpendicular to the ramp is balanced by the normal force, so only the force acting to accelerate the disk down the ramp is the component of the disk's weight parallel to the ramp. This can be found to be
 
<math>f_{grav, x} = Mg \sin \Theta</math>
 
using trigonometry. The friction force therefore has a magnitude of
 
<math>f_{fric, x} = \frac{1}{3} Mg \sin \Theta</math>
 
and opposes the direction the disk's motion, pointing up the ramp.
 
Since we are modeling the disk as a point particle system, we simply treat both of these forces as though they act on the disk's center of mass. The net force acting on the particle is therefore
 
<math>f_{net} = \frac{2}{3} Mg \sin \Theta</math> down the ramp.
 
To find the work done on the particle, we simply multiply the net force by
the displacement of the particle:
 
<math>W = \frac{2}{3} Mg \sin \Theta * d </math>
 
Since the disk had no initial kinetic translational energy, its final translational kinetic energy is equal to the work done on it.
 
<math>\frac{1}{2} M v^2 = \frac{2}{3} Mg \sin \Theta * d </math>
 
<math>v = \sqrt{ \frac{4}{3} g \sin \Theta * d }</math>.
 
===5. (Difficult)===
 
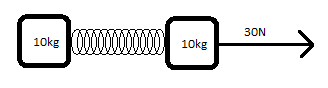
A pair of 10kg masses are connected by a massless spring of unknown spring constant. They begin at rest at the spring's equilibrium length. A 30N rightward force is applied to the mass on the right for 4s. At the end of the 4 second period, the force ceases to act and the mass on the right has traveled 20m. The system continues to travel to the right, and the distance between the two masses oscillates sinusoidally. How much vibrational kinetic energy does the system have? (Vibrational kinetic energy is the energy of the mass' oscillatory movement, as opposed to their translational kinetic energy, which is the energy of the rightward movement of their center of mass.)
 
[[File:Pointparticlesystemtwomass.png]]
 
[https://www.glowscript.org/#/user/YorickAndeweg/folder/PhysicsBookFolder/program/TwoMassSystem Here is a simulation of the system to help you visualize it.]
 
Note: this problem requires the system to be modeled both as a real system and as a point particle system.
 
Solution:
 
Let us first analyze this system as a real system. The work done by the rightward force on the real system is given by its magnitude times the distance traveled by its point of contact, or the rightmost block:
 
<math>W = 30 * 20 = 600</math>Nm.
 
Now, let us treat the system as a point particle system to find the particle's kinetic energy (the real system's translational kinetic energy). We are now modeling the system of two masses as a single point at its center of mass. That is, we are now treating the system as a single mass of 20kg. A 30N force is applied to the particle for 4 seconds, so its acceleration is given by
 
<math>\vec{a} = \frac{\vec{f}}{m} = \frac{3}{2}</math>m/s.
 
and its displacement at the end of the 4 second period is given by
 
<math> d = \frac{1}{2} a t^2 = \frac{1}{2} * \frac{3}{2} * 4^2 = 12</math>m.


I find the entire realm of physics fascinating, and I find it interesting how physicists are constantly coming up with new ways to solve problems and use formulas. The point particle system is a perfect example of that. It can turn a complicated force problem into something easy to approve. I also find it interesting how you can find other forms of energy, such as chemical energy, by using point particle and real systems. Something so small and seemingly unattainable can be found using this method. 
The work done by the rightward force on the point particle system is given by its magnitude times the displacement of that particle:


#How is it connected to your major?
<math>W = 30 * 12 = 360</math>Nm.


I am majoring in Materials Science and Engineering, and there are many ways all different types of physics can be used in MSE. The engineering of materials, specifically being able to calculate the amount and types of energy (and thus the cost) to produce something is absolutely crucial. Point particle systems can make this easier to do, while also adding precision to the calculations.
Recall that the work done on the point particle system represents the increase in translational kinetic energy of the real system, so the system now has 360J of translational kinetic energy.


#An interesting industrial application
It was found earlier that the force imparted a total of 600J of energy to the real system, so <math>600-360=240</math> of the system's joules are oscillatory energy.


As seen in the above examples, there are many real life applications to point particle systems, such as the energy in a person falling, or in a yoyo. This system can also be applied to industry and manufacturing, with the use of various machines that may require gears, levers, or other objects that rotate. Using point particle and real systems, you can calculate the amount of internal energy happening in a moving machine, and therefore how much energy is lost.
==Connectedness==
 
===Scenario: Acrobatics===
 
Consider an acrobat who has jumped from a trampoline and is now on a trajectory through the air. The acrobat is performing a flip and is therefore turning, and they can tuck in or extend their arms in order to affect their moment of inertia and thereby their rotational rate and rotational kinetic energy. Modeling the trajectory of the acrobat may seem complicated, but it can be easily found by modeling the acrobat as a point particle system. When the acrobat is reduced to a point particle, the only force acting on them (ignoring air resistance) is gravity. This means gravity is the only force that can affect the acrobat's translational motion and therefore trajectory, so the acrobat obeys regular [[Projectile Motion]]. Any forces that are present in the real system but not in the point particle system, such as the acrobat's muscles, can only affect the internal energies of the acrobat system, so any movement the acrobat does in the air does not affect their trajectory. This is something acrobats know well; to land in a certain place, they must correctly push off when jumping, and then they are free to do whatever tricks they want while in the air.


== See also ==
== See also ==


===Further reading===
*[[Real Systems]]
*[[Work/Energy]]
*[[Translational, Rotational and Vibrational Energy]]
*[[Center of Mass]]


For more help, a helpful page is: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real
===External links===
 
A helpful page for additional info: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real


A helpful video lecture: https://www.youtube.com/watch?v=T780lL5FlLg&index=41&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y
A helpful video lecture: https://www.youtube.com/watch?v=T780lL5FlLg&index=41&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y


===External links===
An example of another practice problem: https://www.youtube.com/watch?v=FyJTgG3a2hY
 
See also [[Real Systems]] for further information on using Point Particle Systems to solve for the Real Systems.


==References==
==References==
Line 65: Line 208:


Purdue Physics. https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1160/42/5399.
Purdue Physics. https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1160/42/5399.
Yo-yo Clipart: https://www.clipartbest.com


[[Category: Energy]]
[[Category: Energy]]

Latest revision as of 15:14, 3 August 2019

This page describes point particle systems and how they can be used to model certain aspects of a system's motion.

The Main Idea

A point particle system is a physical system, usually composed of multiple parts, modeled as though it were a single particle at its Center of Mass.

When work is done on a system, the energy imparted on it may take on multiple forms. These include Translational, Rotational and Vibrational Energy, Potential Energy, and Thermal Energy. Translational kinetic energy is kinetic energy due to the movement of the system's center of mass. All other types of energy the system has are considered "internal" types of energy because they do not affect the system's motion through its environment, but rather indicate its local properties. Sometimes, when work is done on a system, it imparts both translational kinetic energy and internal types of energy. For example, consider a ball rolling down a ramp. Gravity does work on the ball and increases its energy. It gains some translational kinetic energy (its center of mass gains a velocity down the ramp) and some rotational kinetic energy (its rolling motion causes it to rotate about its center of mass).

Forces acting on a real system can affect both the system's translational acceleration and, depending what part of the system they act on, the internal state of the system. The purpose of modeling a system as a point particle system is to easier to calculate how forces acting on it affect its translational motion through its environment. By modeling the system as a point particle, all forces are assumed to act directly on the system’s center of mass, allowing us to examine only the translational effects of the forces. The net force acting on the point particle causes it to accelerate according to Newton's Second Law: the Momentum Principle.

From an energy perspective, a real system might have multiple types of work done on it at once; it might experience an increase in translational kinetic energy as well as an increase in some types of internal energy. By modeling the system as a point particle, we find only some of the work that is actually done on the system because we look at the displacement of the system's center of mass rather than the part of the system on which the force acts. Specifically, we find the work that affects only its translational kinetic energy because translational kinetic energy is the only energy a system can have when it is reduced to a point particle.

Modeling a system as a point particle offers no insights about the internal state of the system because only forces and work affecting its translational motion can be found.

Point particle systems are in contrast to Real Systems (also known as extended systems), which analyze each part of a system individually instead of reducing it to a single point. Real systems can model a system's internal behavior in addition to its motion through its environment, although they can be very complicated and difficult to analyze quantitatively. Often, to obtain a complete model of a system's behavior, both point-particle and extended models are used.

You may not be aware of it, but you have been modeling systems as point particles for most problems through week 9 because you have mostly been analyzing the translational motion of rigid bodies without regard for their internal energies. Now that we are starting to look at internal types of energy, it becomes more important to separate point particle systems and real systems, and to understand what each model is able to accurately represent.

A Mathematical Model

The mathematical concepts used to analyze point particle systems depend on the system. Often, the work-energy theorem is used. This section explains how to use the work-energy theorem for a point particle system because this is the concept that varies the most significantly from its application to real systems.

The work done on a point particle system is defined as

[math]\displaystyle{ W = \int \vec{F_{net}} \cdot d \vec{r} }[/math],

where [math]\displaystyle{ \vec{r} }[/math] is the position of the particle.

Let us assume that the net force acting on the particle is constant, so that we can get rid of the integral, and that the net force acts in the direction of the particle's motion, so that we can replace the dot product with regular multiplication. This will be the case for most point particle system problems involving work. With these assumptions, the work done on a point particle is given by

[math]\displaystyle{ W = F_{net} * d }[/math]

where [math]\displaystyle{ F_{net} }[/math] is the magnitude of the net force acting on the particle and [math]\displaystyle{ d }[/math] is the distance over which the force is exerted. For point particle systems, that is the distance traveled by the particle. This contrasts with real systems, where the distance over which the force is exerted depends on the movement of particular parts within the system.

The work-energy theorem states that work done on a system increases that system's energy. A point particle cannot experience an increase in internal energy. For example, the moment of inertia of a point particle about its center of mass is 0, so it can have no rotational kinetic energy. This means that all of the work done on a point particle system becomes translational kinetic energy.

In other words, for a point particle system,

[math]\displaystyle{ \Delta KE = F_{net} * d }[/math]

and

[math]\displaystyle{ KE = \frac{1}{2} m v^2 }[/math].

The two equations above are the basis for answering work/energy questions using point particle systems. It is important to remember that when modeling a system as a point particle system, calculating the work done on the system as described above does not find all of the work done on the system, but rather just the work that becomes translational kinetic energy.

Examples

1. (Simple)

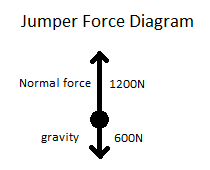
A 60kg person jumps straight up in the air from a crouching position. From the time the person begins to push off of the ground to the time their feet leave the ground, their center of mass moves up 2m, and the normal force between the ground and the person's feet has a constant magnitude of twice the person's weight. Find the velocity of the jumper at the moment their feet leave the ground. Use 10m/s2 for g.

Solution:

Let us model the person as a point particle system. A force diagram for the person would look like this:

The net force acting on the person is the vector sum of the upward normal force and the downward gravitational force, which is a 600N force upwards. This force is constant and in the same direction as the person's motion, so multiplying it by the 2m displacement of the center of mass yields the work done on the person by their muscles:

[math]\displaystyle{ W = 600 * 2 = 1200 }[/math]Nm.

The person begins at rest, so their initial kinetic energy is 0J and their final energy is 1200J.

[math]\displaystyle{ \frac{1}{2} m v^2 = KE }[/math]

[math]\displaystyle{ \frac{1}{2} * 60 * v^2 = 1200 }[/math]

[math]\displaystyle{ v = \sqrt{40} }[/math]m/s.

2. (Middling)

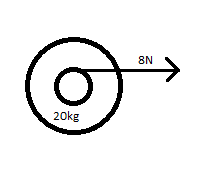
A giant 20kg yo-yo floats at rest in space. Its string (whose mass is negligible compared to the mass of the yo-yo) is pulled with a constant force of 8N. What is the speed of the yo-yo when it has travelled 5m?

Solution:

Solving this problem using energy while treating the system as a real system would be difficult; it would require knowledge of rotational physics and would require more steps. Let us therefore analyze it as a point particle system. This allows us to find only the work done on the yo-yo that is converted to translational kinetic energy.

Treating the yo-yo as a point particle, the work done on it is given by the magnitude of the net force times the particle's displacement:

[math]\displaystyle{ W = 8 * 5 = 40 }[/math]Nm

The point particle's kinetic energy was originally 0, so it is now 40J.

[math]\displaystyle{ KE = \frac{1}{2} m v^2 }[/math]

[math]\displaystyle{ 40 = \frac{1}{2} * 20 * v^2 }[/math]

[math]\displaystyle{ v = 2 }[/math]m/s.

The point particle represents the center of mass of the yo-yo, so it must be moving at 2m/s.

3. (Middling)

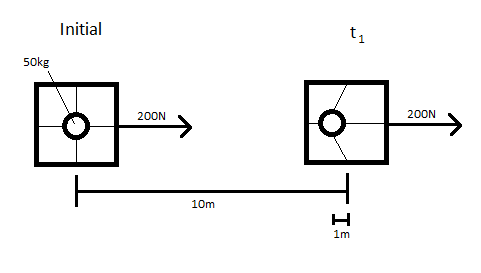
A 50kg metal sphere is suspended in the inside of a large cubic box of negligible mass by six rubber bands- one attaching the sphere to each face of the box. The box and the sphere are initially at rest. A 200N rightward force is applied to the side of the box, causing it to accelerate. At time [math]\displaystyle{ t_1 }[/math], the box has been displaced by 10m to the right. At this time, the sphere is no longer exactly in the center of the box; it is 1m to the left of the center of the box due to its inertia. What is the speed of the sphere at time [math]\displaystyle{ t_1 }[/math]?

Solution:

Let us model the sphere-box system as a point particle system. The center of mass of the system is simply the center of the sphere because the box has negligible mass. The work done on the particle is given by the force acting on the particle times its displacement:

[math]\displaystyle{ W = 200 * 9 = 1800 }[/math]Nm. The displacement of the particle is only 9m because although the box was displaced 10m, the sphere was only displaced 9m due to its inertia and the non-rigidity of its suspension within the box.

The particle initially had no energy, so its energy at time [math]\displaystyle{ t_1 }[/math] is 1800J.

[math]\displaystyle{ KE = \frac{1}{2} m v^2 }[/math]

[math]\displaystyle{ 1800 = \frac{1}{2} * 50 * v^2 }[/math]

[math]\displaystyle{ v = \sqrt{72} }[/math]m/s.

4. (Middling)

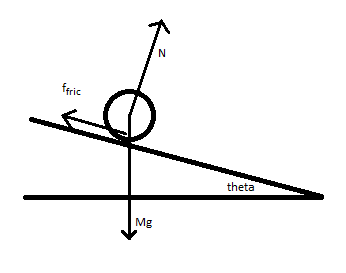
A uniform disk of mass [math]\displaystyle{ M }[/math] starts at rest and rolls without slipping down a ramp. The plane of the ramp makes an angle of [math]\displaystyle{ \Theta }[/math] with the horizontal. The force of Static Friction acting on the bottom of such a disk, causing it to rotate, always has a magnitude of 1/3 the force acting to move the disk down the ramp. What is the translational speed of the disk after it has traveled a distance of [math]\displaystyle{ d }[/math] diagonally down the ramp?

Solution:

Let us analyze this system as a point particle system because we are only interested in its translational motion.

The component of the disk's weight perpendicular to the ramp is balanced by the normal force, so only the force acting to accelerate the disk down the ramp is the component of the disk's weight parallel to the ramp. This can be found to be

[math]\displaystyle{ f_{grav, x} = Mg \sin \Theta }[/math]

using trigonometry. The friction force therefore has a magnitude of

[math]\displaystyle{ f_{fric, x} = \frac{1}{3} Mg \sin \Theta }[/math]

and opposes the direction the disk's motion, pointing up the ramp.

Since we are modeling the disk as a point particle system, we simply treat both of these forces as though they act on the disk's center of mass. The net force acting on the particle is therefore

[math]\displaystyle{ f_{net} = \frac{2}{3} Mg \sin \Theta }[/math] down the ramp.

To find the work done on the particle, we simply multiply the net force by the displacement of the particle:

[math]\displaystyle{ W = \frac{2}{3} Mg \sin \Theta * d }[/math]

Since the disk had no initial kinetic translational energy, its final translational kinetic energy is equal to the work done on it.

[math]\displaystyle{ \frac{1}{2} M v^2 = \frac{2}{3} Mg \sin \Theta * d }[/math]

[math]\displaystyle{ v = \sqrt{ \frac{4}{3} g \sin \Theta * d } }[/math].

5. (Difficult)

A pair of 10kg masses are connected by a massless spring of unknown spring constant. They begin at rest at the spring's equilibrium length. A 30N rightward force is applied to the mass on the right for 4s. At the end of the 4 second period, the force ceases to act and the mass on the right has traveled 20m. The system continues to travel to the right, and the distance between the two masses oscillates sinusoidally. How much vibrational kinetic energy does the system have? (Vibrational kinetic energy is the energy of the mass' oscillatory movement, as opposed to their translational kinetic energy, which is the energy of the rightward movement of their center of mass.)

Here is a simulation of the system to help you visualize it.

Note: this problem requires the system to be modeled both as a real system and as a point particle system.

Solution:

Let us first analyze this system as a real system. The work done by the rightward force on the real system is given by its magnitude times the distance traveled by its point of contact, or the rightmost block:

[math]\displaystyle{ W = 30 * 20 = 600 }[/math]Nm.

Now, let us treat the system as a point particle system to find the particle's kinetic energy (the real system's translational kinetic energy). We are now modeling the system of two masses as a single point at its center of mass. That is, we are now treating the system as a single mass of 20kg. A 30N force is applied to the particle for 4 seconds, so its acceleration is given by

[math]\displaystyle{ \vec{a} = \frac{\vec{f}}{m} = \frac{3}{2} }[/math]m/s.

and its displacement at the end of the 4 second period is given by

[math]\displaystyle{ d = \frac{1}{2} a t^2 = \frac{1}{2} * \frac{3}{2} * 4^2 = 12 }[/math]m.

The work done by the rightward force on the point particle system is given by its magnitude times the displacement of that particle:

[math]\displaystyle{ W = 30 * 12 = 360 }[/math]Nm.

Recall that the work done on the point particle system represents the increase in translational kinetic energy of the real system, so the system now has 360J of translational kinetic energy.

It was found earlier that the force imparted a total of 600J of energy to the real system, so [math]\displaystyle{ 600-360=240 }[/math] of the system's joules are oscillatory energy.

Connectedness

Scenario: Acrobatics

Consider an acrobat who has jumped from a trampoline and is now on a trajectory through the air. The acrobat is performing a flip and is therefore turning, and they can tuck in or extend their arms in order to affect their moment of inertia and thereby their rotational rate and rotational kinetic energy. Modeling the trajectory of the acrobat may seem complicated, but it can be easily found by modeling the acrobat as a point particle system. When the acrobat is reduced to a point particle, the only force acting on them (ignoring air resistance) is gravity. This means gravity is the only force that can affect the acrobat's translational motion and therefore trajectory, so the acrobat obeys regular Projectile Motion. Any forces that are present in the real system but not in the point particle system, such as the acrobat's muscles, can only affect the internal energies of the acrobat system, so any movement the acrobat does in the air does not affect their trajectory. This is something acrobats know well; to land in a certain place, they must correctly push off when jumping, and then they are free to do whatever tricks they want while in the air.

See also

External links

A helpful page for additional info: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real

A helpful video lecture: https://www.youtube.com/watch?v=T780lL5FlLg&index=41&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y

An example of another practice problem: https://www.youtube.com/watch?v=FyJTgG3a2hY

References

Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.

Purdue Physics. https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1160/42/5399.

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Point_Particle_Systems&oldid=36812"