Thermal Energy

Claimed by Erin Yoon (Spring 2023)

Main Idea

All objects are made up of atoms and molecules-- so many that it would take longer than the Universe's estimated lifetime to count. The constant and random motion of an object's atoms or molecules is what determines its Thermal Energy. Thermal Energy is a component of internal energy, but is unrelated to the vibrational and rotational energy of a solid's atoms. Instead, Thermal Energy occurs from atoms' translational motion.

When we say "change of thermal energy," we mean that it is the part of the internal energy that is associated with a Temperature change. Thermal Energy is quantified using temperature. This quantification describes the approximate average Thermal Kinetic Energy present in all of the atoms or molecules in the object/sample/system. In the real world, it is often impossible to accurately state how much of an object's internal energy is Thermal. However, if the Heat Capacity and mass of am object is known, we can measure its temperature using a thermometer and calculate its Thermal Energy.

A Mathematical Model

A change in Thermal Energy can be calculated by using the following equation:

[math]\displaystyle{ \Delta Q = mC \Delta T }[/math], where

[math]\displaystyle{ Q }[/math] is the thermal energy in Joules ([math]\displaystyle{ J }[/math])

[math]\displaystyle{ m }[/math] is the mass of an object in Grams ([math]\displaystyle{ g }[/math])

[math]\displaystyle{ C }[/math] is the object's Specific Heat Capacity in [math]\displaystyle{ \frac{J}{g \ °C} }[/math]

[math]\displaystyle{ \Delta T }[/math] is the change in object's temperature in Celsius ([math]\displaystyle{ °C }[/math])

This equation states:

The change in Thermal Energy of a system is equal to the mass of said system times the Specific Heat Capacity of said material of the system times the change in Temperature of said system.

Temperature

In order to quantify Thermal Energy, a measurement of the average translational energy of the atoms or molecules in a system is measured. This value is referred to as temperature. In order to measure temperature, a thermometer of some sort must be utilized. The most well known representation of a thermometer is a thin glass column filled with either mercury or an alcohol. When a thermometer is placed into a system and time passes, the average kinetic energies of the system and the thermometer become the same. The change in thermal energy causes the alcohol or mercury to expand or compress. The temperature is then measured on a scale of Celsius, Kelvin, or Fahrenheit.

Specific Heat Capacity

Specific heat capacity is a value unique to each object or material that quantifies the amount of thermal energy it takes to raise the temperature of said object by one degree Celsius. For example, water's specific heat capacity is 4.186[math]\displaystyle{ \frac{J}{g \ °C} }[/math], meaning that it takes 4.186 Joules of Thermal Energy to raise the temperature of water by one degree Celsius. Materials with higher specific heat capacity, thus, require more Thermal Energy to increase in temperature than materials with lower specific heat capacity. This principle also applies when materials are cooling down in the absence of heat-- materials with higher specific heat capacity will lose heat energy (and decrease in temperature) more slowly than materials with lower specific heat capacity.

The Kinetic Molecular Theory of Matter

The Idea of Thermal Energy is derived from the Kinetic Molecular Theory of Matter (KMToM). This theory explains why matter can and does exist in different phases. It also provides a description of the interactions and properties of atoms via ideas generally applied to macroscopic systems. According to the KMToM, all matter is comprised of lots of smaller molecules or atoms that are constantly moving. The type of motion of these particles is a result of the Thermal Energy present, and it determines whether the substance is in a gaseous, liquid, solid, or plasma state. When energy is introduced or lost from a material, the resulting change in motion of the individual particles can cause a phase change to occur for the substance, by increasing or decreasing the spacing between atoms and molecules. If enough energy is added to the substance, intermolecular forces can be overcome, leading to a plasmic state.

Ways to Transfer Thermal Energy

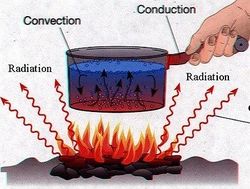
Convection: The movement in fluids (gases and liquids) caused by gravity, in which hotter fluids (less dense) rise, and cooler fluids (denser) sink, causing an increased transfer of Heat or Thermal Energy. For example, clouds are created by rising, warmed water (evaporation). These clouds move up and down in the atmosphere based on how dense they are, until they become too dense and rain on us (precipitation).
Conduction: The transfer of Heat or Thermal Energy caused by the direct touching of two separate objects. For example, when you sit down in a seat and feel it is warm, this is due to the seat being warmer than your pants, and thus transferring its Heat to you by conduction.
Radiation: The transfer of heat over a distance, between two objects that are not touching. Electromagnetic Radiation warms an object by transferring some of its energy to the object. For example, how does the Sun warm the Earth? The Earth and Sun are not touching, so it can't be conduction. Furthermore, the Earth and Sun are not a part of the same fluid that transfers Heat between them, so it is not Convection. Therefore, the Sun warms the Earth through seemingly endless amounts of Radiation bombarding the Earth constantly.

Thermal Equilibrium

Like all systems in nature, Thermal Energy works to reach Thermal Equilibrium. When two substances of differing temperatures come into "contact," the substance of greater Thermal Energy will do microscopic work on the other substance until the two are at the same temperature. Atoms of the higher energy substance will collide with those of the lower energy substance at the boundary. Kinetic energy will be transferred and distribute evenly throughout. Given enough time, this process of propagation of kinetic energy will continue until Thermal Equilibrium is reached. However, do not think that because two substances have reached Thermal Equilibrium that they are not transferring Thermal Energy. Instead, they are continuously transferring Thermal Energy with each other, but at an equal rate, so that neither's Thermal Energy/Temperature changes. The transfer of Thermal Energy is referred to as Heat.

Computational Model

PhET by the University of Colorado Boulder allows free public usage of their simulations in an educational context. Their simulation Energy Forms and Changes is a useful visual companion to practice calculating specific heat capacities and thermal energies of materials.

Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu).

Examples

Simple

[math]\displaystyle{ 500 g }[/math] of water is heated from an initial temperature [math]\displaystyle{ T_0 = 20°C }[/math] to a final temperature [math]\displaystyle{ T_f = 50°C }[/math].

a) What is the change in Thermal Energy ([math]\displaystyle{ \mathbf{\vartriangle}Q }[/math]) of water? (The Heat Capacity of water is [math]\displaystyle{ 4.2 \frac{J}{g°C} }[/math])

We know a general formula for the change in Thermal Energy of a substance from our Mathematical Model:

[math]\displaystyle{ \Delta Q = mC \Delta T }[/math]

We know the initial and final temperatures of the sample of water, so we can find the change in temperature of the water:

[math]\displaystyle{ \mathbf{\vartriangle}T = T_f - T_0 = 50°C - 20°C = 30°C }[/math]

Our equation now only has 1 unknown, the change in Thermal Energy. Therefore, we can calculate it:

[math]\displaystyle{ \Delta Q = mC \Delta T = 500 \times 4.2 \times 30 = 63,000 \ J }[/math]

Middling

[math]\displaystyle{ 400 g }[/math] of water, with an initial temperature of [math]\displaystyle{ T_{0_{w}} = 90°C }[/math] [math]\displaystyle{ \left(C = 4.2 \ \frac{J}{g°C}\right) }[/math] is poured into an aluminum pan, whose mass is [math]\displaystyle{ 800 g }[/math] with an initial temperature of [math]\displaystyle{ T_{0_{a}} = 20°C }[/math] [math]\displaystyle{ \left(C = 0.9 \ \frac{J}{g°C}\right) }[/math].

a) After a few minutes, what is the temperature of the water ([math]\displaystyle{ T_{w_{f}} }[/math]), assuming the pan and water are thermally insulated from their surroundings?

We know from the Energy Principle that the change in energy of the system and its surroundings is 0:

[math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]

If we choose the water and the aluminum pan as the system, and nothing as the surroundings (no energy loss/work done), we end up with:

[math]\displaystyle{ \Delta E_{system} = 0 }[/math]

Separating the system into its components gives:

[math]\displaystyle{ \Delta E_{w} + \Delta E_{a} = 0 }[/math]

Next, we solve for the change in energy of the sample of water:

[math]\displaystyle{ \Delta E_{w} = - \Delta E_{a} }[/math] (1)

We know the change in energy of the water is due to a change in Thermal Energy, since it is only sitting in the pan and being cooled by the aluminum pan. We know a quantitative way to describe this change in Thermal Energy:

[math]\displaystyle{ \Delta Q = mC \Delta T }[/math]

Furthermore, the change in Thermal Energy Is equal to the change in energy of the water, since no work is being done on the system. This also applies to the stationary aluminum pan. Therefore, we can rewrite equation 1 as:

[math]\displaystyle{ \Delta Q_{w} = - \Delta Q_{a} }[/math]

or:

[math]\displaystyle{ m_{w}C_{w} \Delta T_{w} = -m_{a}C_{a} \Delta T_{a} }[/math]

We need to find the final temperature of the sample of water ([math]\displaystyle{ T_{w_{f}} }[/math]). We can do this by expanding the term [math]\displaystyle{ \Delta T_{w} }[/math]:

[math]\displaystyle{ m_{w}C_{w}\left(T_{w_{f}} - T_{w_{i}} \right) = - m_{a}C_{a}\left(T_{a_{f}} - T_{a_{i}} \right) }[/math] (2)

NOTE, after a few minutes, the aluminum pan and the sample of water will almost be in Thermal Equilibrium. This gives us the ability to simplify the two unknowns ([math]\displaystyle{ T_{w_{f}} \ \text{and} \ T_{a_{f}} }[/math]) into one unknown:

[math]\displaystyle{ T_{f} \approx T_{w_{f}} \quad T_{f} \approx T_{a_{f}} }[/math]

This simplifies 2 in the following way:

[math]\displaystyle{ m_{w}C_{w}T_{f} - m_{w}C_{w}T_{w_{i}} = -m_{a}C_{a}T_{f} + m_{a}C_{a}T_{a_{i}} }[/math]

[math]\displaystyle{ m_{w}C_{w}T_{f} + m_{a}C_{a}T_{f} = m_{w}C_{w}T_{w_{i}} + m_{a}C_{a}T_{a_{i}} }[/math]

[math]\displaystyle{ T_{f} \left(m_{w}C_{w} + m_{a}C_{a} \right) = m_{w}C_{w}T_{w_{i}} + m_{a}C_{a}T_{a_{i}} }[/math]

[math]\displaystyle{ T_{f} = \frac{m_{w}C_{w}T_{w_{i}} + m_{a}C_{a}T_{a_{i}}}{m_{w}C_{w} + m_{a}C_{a}} }[/math]

Plugging in known values gives:

[math]\displaystyle{ T_{f} = \frac{(400 \times 4.2 \times 90) + (800 \times 0.9 \times 20)}{(400 \times 4.2) + (800 \times 0.9)} = 69 \ °C }[/math]

Difficult

[math]\displaystyle{ 500g }[/math] of water with an initial temperature of [math]\displaystyle{ T_{w_{0}} = 87 \ °C \left(C = 4.2 \ \frac{J}{g°C}\right) }[/math] is poured into an aluminum pan whose mass is [math]\displaystyle{ 800g }[/math] with an initial temperature of [math]\displaystyle{ T_{a_{0}} = 22 \ °C \left(C = 0.9 \ \frac{J}{g°C}\right) }[/math]. The aluminum pan and water are allowed to reach Thermal Equilibrium. Then, you place the pan on a hot electric stove. While the stove is heating the pan, you stir the water doing [math]\displaystyle{ 26,000 \ J }[/math] of work, raising the temperature of the system to [math]\displaystyle{ 82.5 \ °C }[/math].

a) How much energy transfer due to a temperature difference was there from the stove into the system consisting of the water and the pan?

First, we need to find the final temperature of the water and aluminum pan system, which is in Thermal Equilibrium. We start this in the same fashion as the Middling example:

[math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]

At this step, there is no interaction between the surroundings and the system (pan & water):

[math]\displaystyle{ \Delta E_{system} = 0 }[/math]

Splitting this into components gives:

[math]\displaystyle{ \Delta E_{w} + \Delta E_{a} = 0 }[/math]

Pluggin in [math]\displaystyle{ \Delta E = \Delta Q = mC \Delta T }[/math] for each part of the system gives:

[math]\displaystyle{ m_{w}C_{w} \Delta T_{w} + m_{a}C_{a} \Delta T_{a} = 0 }[/math]

We know in Thermal Equilibrium the temperature of the system will be the same throughout. Therefore, the final temperature of the water and the pan will be the same:

[math]\displaystyle{ T_{w_{f}} = T_f = T_{a_{f}} }[/math]

[math]\displaystyle{ m_{w}C_{w}(T_{f} - T_{w_{i}}) + m_{a}C_{a}(T_{f} - T_{a_{i}}) = 0 }[/math]

[math]\displaystyle{ T_f (m_{w}C_{w} + m_{a}C_{a}) = m_{w}C_{w}T_{w_{i}} + m_{a}C_{a}T_{a_{i}} }[/math]

[math]\displaystyle{ T_f = \frac{m_{w}C_{w}T_{w_{i}} + m_{a}C_{a}T_{a_{i}}}{m_{w}C_{w} + m_{a}C_{a}} = \frac{(500 \times 4.2 \times 87) + (800 \times 0.9 \times 22)}{(500 \times 4.2) + (800 \times 0.9)} = 70.404 \ °C }[/math]

Now, we assert the Energy Principle again, with the system being the water and the pan. The surrounding that does work on the system is the stirring rod. It does [math]\displaystyle{ 26,000 \ J }[/math] of work. We also have Heat being added to the system through conduction between the hot stove and the pan. Using the Energy Principle, we see:

[math]\displaystyle{ \Delta E_{system} = W_{surroundings} + Q_{stove} }[/math]

or:

[math]\displaystyle{ \Delta Q_{system} = W_{stirrer} + Q_{stove} }[/math]

We know the system's change in Thermal Energy is made of up of the change in Thermal Energy of its constituents:

[math]\displaystyle{ \Delta Q_{w} + \Delta Q_{a} = W_{stirrer} + Q_{stove} }[/math]

We can solve for the Heat Energy added to the pan and water from the stove:

[math]\displaystyle{ Q_{stove} = \Delta Q_{w} + \Delta Q_{a} - W_{stirrer} }[/math]

We know the equation for a change in Thermal Energy from our Mathematical Model:

[math]\displaystyle{ Q_{stove} = m_{w}C_{w}(T_{w_{f}} - T_{w_{i}}) + m_{a}C_{a}(T_{a_{f}} - T_{a_{i}}) - W_{stirrer} }[/math]

Once again, the final temperatures of the pan and water system are the same, [math]\displaystyle{ T_{f} = 82.5 \ °C }[/math]. The initial temperature of the system, which we found as the final temperature of the first part of the problem, is [math]\displaystyle{ T_{i} = 70.404 \ °C }[/math]. This leads to:

[math]\displaystyle{ Q_{stove} = (T_{f} - T_{i})(m_{w}C_{w} + m_{a}C_{a}) - W_{stirrer} }[/math]

Plugging in all knowns gives the answer:

[math]\displaystyle{ Q_{stove} = (82.5 - 70.404)(500 \times 4.2 + 800 \times 0.9) - 26000 = 8,111 \ J }[/math]

Connectedness

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Thermal Energy is a phenomenon present in all aspects of life. Everything from the Sun to an ice cube contains, emits, and absorbs thermal energy. In order to convert thermal energy to other, more useful forms an engine must be used. For example, steam carries a large amount of thermal energy, which can be used mechanically via steam engines. Similarly, Thermal Energy is integral in determining which phase of matter a material exists in. For example, at left is a phase diagram of iron-- it can be seen from the axes that what phase iron is in is determined by the surrounding pressure and the iron's temperature.

One of the interesting industrial application of thermal energy is industrial thermal energy storage. Thermal energy storage is a technology that stocks thermal energy by heating or cooling a storage medium so that the stored energy can be used at a later time for heating and cooling applications and power generation.

History

Thermal Energy was discovered by a man named James Joule in the 1840's. Careful experiments showed that the temperature increase of an object and its surroundings due to friction is directly related to the amount of mechanical energy lost. Joule carried out one of the most famous experiments, demonstrating this fact. Joule hung some weights from pulleys, so that as they fell, they turned a paddle-wheel apparatus immersed in a bucket of water. The friction between the paddles and the water raised the water’s temperature by an amount that was directly proportional to the distance that the weights fell. In our modern system of units, Joule found that raising the temperature of a kilogram of water by one degree Celsius required a loss in mechanical (gravitational) energy of approximately 4,200 Joules. Joule therefore proposed that this mechanical energy is not actually lost, but converted into a new type of energy: Thermal Energy, which manifests itself as an increase or decrease in temperature.

https://www.sciencedirect.com/topics/engineering/specific-heat-capacity

https://commons.wikimedia.org/wiki/File:Pure_iron_phase_diagram_(EN).svg