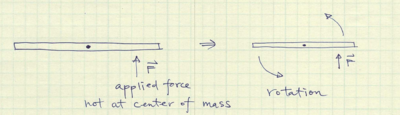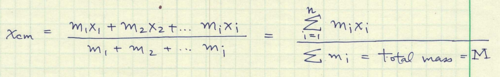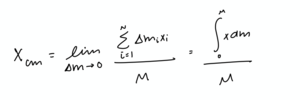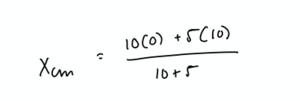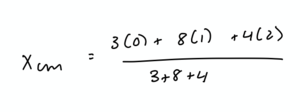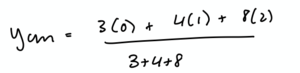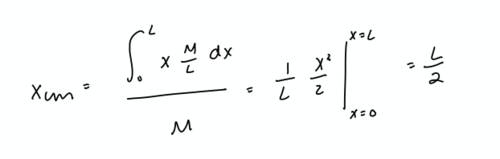Center of Mass
The Main Idea
The center of mass of an object is the point in space where if a force was applied, the object moves according to Newton's laws without rotation. At the center of mass, the distribution of mass is balanced and the average of the weighted position coordinates of the distributed mass defines its coordinates. Mechanical calculations are often simplified with respect to the center of mass of objects. [5]
When a force is applied not to the center of mass:
A Mathematical Model
The position of the center of mass of an object can be found by summating the product of each point mass and its relative linear position and dividing by the sum by the total mass.
This equation can then be extended to three dimensions.
When calculating the center of mass for a continuous distribution of mass, the expression becomes an infinite sum that can be expressed in the form of an integral. [6]
A Computational Model
Center of mass can be a powerful tool for simplifying problems in physics. Similarly, using VPython (or any other programming language, for that matter), using concepts related to center of mass can greatly simplify code. Simply finding the center of mass of a virtual object can be very simple for an object with uniform mass and volume, however if that is changing, an iterative process for finding center of mass may need to be implemented.
For more information on iteration and coding, visit this page: VPython Loops. It is an important concept in this course and is one very easily adapted to center of mass concepts.
Velocity, Momentum, and Kinetic Energy with Center of Mass
If you know the center of mass, you can use this center of mass to find other quantities associated with the motion of the multiparticle system.
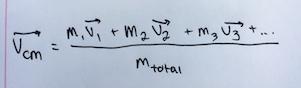
If the velocity of the center of mass is much less than the speed of light:

To extend this knowledge to translational kinetic energy for a multiparticle system:
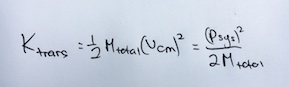
Examples
Simple
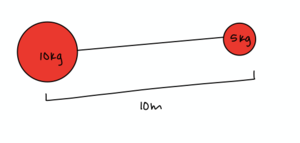
A 10 kg point mass and a 5 kg point mass are connected by a 10 m massless rod.
Find the center of mass. This is example of a 1-dimensional center of mass problem.
Solution
First, we will need to establish an origin. For simplicity, we will establish the left end, the position of the 10 kg point mass, as the origin. Relative to the origin, the position of the 10 kg mass is 0 m and the position of the 5 kg mass is 10 m. Placing these values into our formula for 1-dimensional center of mass, we get:
Therefore, the center of mass is 10/3 m from the left end of the rod. It is important to state your distances relative to your stated origin.
Middling
Considering a system with the three particles: m1 = 2 kg, v1 = < 10, -5, 14 > m/s m2 = 9 kg, v2 = < -13, 6, -6 > m/s m3 = 5 kg, v3 = < -29, 34, 23 > m/s
and given the momentum Ptotal = <-242, 214, 89>, find the velocity of the center of mass.
Solution
Starting from the equation Ptotal = Mtotal(Vcm)
We have Ptotal, which is <-242, 214, 89>, and Mtotal, which is 2 + 5 + 9 = 16. Substituting these values into the center of mass momentum equation, we see that:
<-242, 214, 89> = (2 + 5 + 9)(Vcm)
and Vcm = <-242, 214, 89> / 16
Therefore, Vcm = <-15.125, 13.375, 5.56>.
Moderate
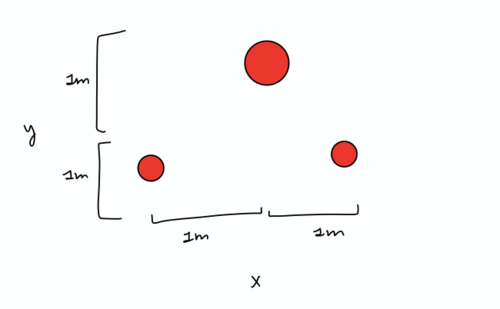
3 point masses are placed on the x-y plane as shown:
Find the center of mass. This is an example of a 2-dimensional center of mass problem.
Solution
This problem is similar to the last problem except that we will need to find BOTH the x and y components of the center of mass. Like before, we need to establish an origin. For simplicity, we will establish the lower left corner, the position of the 3 kg mass as the origin. Then, we need to solve the two directions separately. We will start with the x direction. Relative to the origin, the 3 kg mass is at 0 m, the 8 kg mass is at 1 m, and the 4 kg mass is at 2 m. Placing these values into our center of mass of point masses formula, we get:
Therefore, the center of mass lies 16/15 m from the origin in the x direction.
Next, we will solve for the y direction. Relative to the origin, the 3 kg mass is at 0 m, the 4 kg mass is at 1 m, and the 8 kg mass is at 2 m. Placing these values into our center of mass of point masses formula, we get:
Therefore, the center of mass lies 4/3 m from the origin in the y direction.
The center of mass lies at the coordinates (16/15 m, 4/3 m).
Difficult
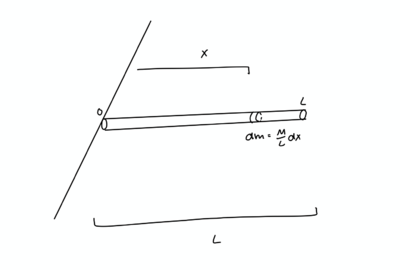
Find the x component of the center of mass of a uniform rod of length L and mass M with continuous, uniform mass. This is an example of a continuous mass problem.
Solution
For this problem, we need to use the continuous mass formula. As shown in the diagram, the dm component can be represented by M/L dx because the mass in the rod is uniformly distributed. Therefore, our equation becomes:
Therefore, the center of mass lies at L/2, which agrees with the rule of symmetry for uniform masses.
Connectedness
The main purpose of using the center of mass is to simplify irregular objects into point masses. Force diagrams are based on this idea, and this aids in the calculation of motion of complex objects. For biomedical engineering majors, we can use the center of mass of body parts in order to simplify the motion of body parts.
ADD MORE INFO ABOUT CONNECTEDNESS HERE
History
The concept of center of mass was first introduced by Archimedes while he worked to simplify assumptions about gravity that amounted to a uniform field, thus arriving at the mathematical properties of the center of mass. In an experiment, Archimedes observed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point—their center of mass. He developed mathematical techniques for finding the centers of mass of objects of uniform density of various well-defined shapes. Additionally, Euler's first law of motion states exactly what was what mentioned in the "Velocity, Momentum, and Kinetic Energy with Center of Mass" section. Leonhard Euler formulated his laws of motion after Newton did, and stated that the linear momentum of a multiparticle system (Ptotal) is equal to the total mass of the multiparticle system (Mtotal) times the velocity of the center of mass of the multiparticle system (Vcm). Therefore, Ptotal = Mtotal(Vcm). [7]
See also
Further reading
Mass [1]
Force [2]
Moment of Inertia [3]
Torque [4]
References
PhysicsLab [5]
HyperPhysics [6]
Wikipedia [7]