Kinetic Energy
Claimed by ilukowiecki3 Spring 2020
Introduction
Objects in motion have energy associated with them. This energy of motion is called kinetic energy. Kinetic energy, often abbreviated as KE, is usually given in the standard S.I. units of Joules (J). KE is also given in units of kilo Joules (kJ). [math]\displaystyle{ 1 kJ = 1000 J }[/math]. [math]\displaystyle{ 1 J = 1 kg*(m²/s²) }[/math]. Other types of energy include Rest Mass Energy and Potential Energy. Kinetic energy is also known as the work needed to accelerate a mass from rest to a final velocity. Once the object reaches this speed, the kinetic energy remains constant unless the speed is changed.
Kinetic energy can take many forms, such as vibrational kinetic energy, rotational kinetic energy, and translational kinetic energy. Vibrational kinetic energy is the energy due to vibrational motion, while rotational kinetic energy is the energy due to rotational motion. Translational kinetic energy, the focus of this wiki page, is energy due to motion from place to place. More information on these three kinds of kinetic motions can be found at Translational, Rotational, and Vibrational Energy. Kinetic energy does not have a direction and is a scalar value. It is not a vector quantity but is rather a magnitude. Kinetic energy can be also be transferred into other types of energy, such as potential energy or chemical energy. In order to gain kinetic energy, a force must be applied, which causes work to be done on an object. This work causes the object to move, which is referred to as kinetic energy. The value of kinetic energy depends on the relationship between the object in question and the point of observation/the related frame of reference.
Rest Energy
Rest energy can be defined as the energy of an object at rest. To find the rest energy of an object/particle, multiply the mass by its velocity squared (E = mv²). This is the correct form of Einstein’s most famous equation, which shows that energy is related to the mass of an object at rest. For example, if energy is stored in the object, its rest mass increases. This also implies that mass can be destroyed to release energy.
Does this mean that only objects with mass have energy? NO! there is an equation that helps us understand this topic, Einstein's Relativistic Mass Formula. E² = (pc)² + (mc²)². When the mass = 0, E = pc
Mathematical Model
The relativistic equation for kinetic energy according to Einstein's Theory of Relativity is [math]\displaystyle{ KE=mc²(\frac{1}{\sqrt{1-\frac{v²}{c²}}} -1) }[/math]. However, for cases where an object's velocity is far less than the speed of light ([math]\displaystyle{ 3X10^8 m/s }[/math]), one can use the simplified kinetic energy formula as an approximation: [math]\displaystyle{ KE=\frac{1}{2}mv² }[/math]. In most cases, the simplified kinetic energy formula gives a result with only minimal error. However, for near light-speed calculations, such as those involving subatomic particles such as electrons, protons, or photons, the relativistic equation must be used. Usually, the simplified kinetic energy formula is used to calculate the kinetic energy of an average object and will be used in almost all cases in introductory physics.
A Computational Model
By Conservation of Energy, energy can be converted, but it cannot be created nor destroyed. Hence, in an isolated system, energy can continuously be converted back and forth between potential and kinetic energy without any loss. The following link is an excellent visualization of energy that can be demonstrated with v-python. The spring will oscillate up and down constantly converting between Elastic Potential Energy and Kinetic Energy. https://trinket.io/glowscript/87a35d5778

Examples
Simple
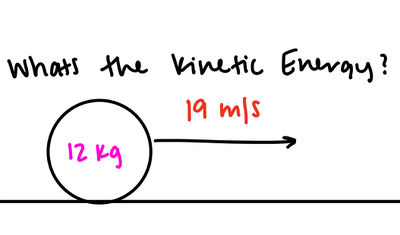
A ball is rolling along a frictionless surface at a constant [math]\displaystyle{ 19 m/s }[/math]. The ball has mass [math]\displaystyle{ 12 kg }[/math]. What is the kinetic energy of the ball in Joules?
Solution:
- Because the ball's velocity is far less than the speed of light, we can use the simplified kinetic energy formula.
- [math]\displaystyle{ KE=\frac{1}{2}mv² }[/math]
- [math]\displaystyle{ KE=\frac{1}{2}(12 kg)*(19 m/s)² }[/math]
- Hence, KE = [math]\displaystyle{ 2166 J }[/math] or [math]\displaystyle{ 2.166 kJ }[/math]
Middling
An electron is moving through space at a constant [math]\displaystyle{ 2.9X10^8 m/s }[/math]. The electron has mass [math]\displaystyle{ 9.1X10^-31 kg }[/math]. What is the kinetic energy of the ball in Joules?
Solution:
- Because the electron's velocity is close to the speed of light, we must use the relativistic kinetic energy formula.
- [math]\displaystyle{ KE=mc²(\frac{1}{\sqrt{1-\frac{v²}{c²}}} -1) }[/math]
- [math]\displaystyle{ KE=(9.1X10^-31 kg)(3X10^8 m/s)²(\frac{1}{\sqrt{1-\frac{(2.9X10^8 m/s)²}{(3X10^8 m/s)²}}} -1) }[/math]
- Hence, KE = [math]\displaystyle{ 2.38X10^-13 J }[/math] or [math]\displaystyle{ 2.38X10^-16 kJ }[/math]
Difficult
An proton is moving through space at constant velocity. It is found to have kinetic energy [math]\displaystyle{ 2.38X10^-15 J }[/math]. The proton has mass [math]\displaystyle{ 1.67X10^-27 kg }[/math]. What is the proton's velocity?
Solution:
- Because we are dealing with a subatomic particle, we should probably use the relativistic kinetic energy formula as the approximate kinetic energy formula may be very inaccurate if the particle is moving at a velocity near the speed of sound.
- [math]\displaystyle{ KE=mc²(\frac{1}{\sqrt{1-\frac{v²}{c²}}} -1) }[/math]
- [math]\displaystyle{ \frac{KE}{mc²}=(\frac{1}{\sqrt{1-\frac{v²}{c²}}} -1) }[/math]
- [math]\displaystyle{ \frac{KE}{mc²} + 1=\frac{1}{\sqrt{1-\frac{v²}{c²}}} }[/math]
- [math]\displaystyle{ \frac{1}{\frac{KE}{mc²} + 1}=\sqrt{1-\frac{v²}{c²}} }[/math]
- [math]\displaystyle{ 1-\frac{v²}{c²}=(\frac{1}{\frac{KE}{mc²} + 1})² }[/math]
- [math]\displaystyle{ \frac{v²}{c²}=1 - (\frac{1}{\frac{KE}{mc²} + 1})² }[/math]
- [math]\displaystyle{ v²=c²*(1 - (\frac{1}{\frac{KE}{mc²} + 1})²) }[/math]
- [math]\displaystyle{ v=\sqrt{c²*(1 - (\frac{1}{\frac{KE}{mc²} + 1})²)} }[/math]
- [math]\displaystyle{ v=c*\sqrt{1 - (\frac{1}{\frac{KE}{mc²} + 1})²} }[/math]
- [math]\displaystyle{ v=3X10^8 m/s*\sqrt{1 - (\frac{1}{\frac{(2.38X10^-15 J)}{(1.67X10^-27 kg)(3X10^8 m/s)²} + 1})²} }[/math]
- v = [math]\displaystyle{ 2.999X10^8 m/s }[/math]. This means that the proton is moving very close to the speed of light and hence our choice to use the relativistic kinetic energy equation was a good one.
Connectedness
Kinetic energy is very important in baseball. When a batter hits a ball, kinetic energy from the bat is transferred into the ball. leading to the ball flying out into the field. Assuming solid contact between the ball and the bat, the amount of kinetic energy transferred to the ball is directly proportional to the kinetic energy of the bat. As this is a non-relativistic application, there are only two variables to consider when calculating the kinetic energy of the bad: m and v. While a heaver bat would have greater kinetic energy than a bat of smaller mass traveling at the same velocity, heavier bats are more difficult to swing quickly and generally have lower velocity. Hence, batters must try to choose the a bat that they can swing very fast that still has reasonable mass to it to try to maximize kinetic energy ([math]\displaystyle{ \frac{1}{2}mv² }[/math]). https://www.youtube.com/watch?v=zDcf7eEaP0M
Kinetic energy also plays a role in horse-back riding. For instance, a horse's jump happens in three parts.
First, at the beginning of the jump, the horse tenses its muscles and kicks off the ground to lift into the air, converting chemical energy into horizontal and vertical kinetic energy. While in the air, the horse's horizontal kinetic energy doesn't change, but its vertical kinetic energy is converted into gravitational potential energy until it reaches the apex of the jump. As the horse falls, this gravitational potential is converted back into kinetic energy. Finally, when the horse lands, the horse's legs absorb the impact and slow down slightly by converting the vertical and some of the horizontal kinetic energy into heat.
Kinetic energy is also important to biomedical engineering. Biomedical engineering, such as the design of prosthetics, must focus on how humans move and produce kinetic energy in order to make the best prosthetic for a person.
The biomedical engineer must consider how much energy the person will need to move the prosthetics, how heavy the mass of the prosthetic must be to be efficient, and how much energy must continuously be applied to keep the prosthetic moving.
History
Kinetic energy can be traced all the way back to Aristotle (384 BCE to 322 BCE) who first proposed the concept of actuality and potentiality (actuality being kinetic energy and potentiality being Potential Energy). The connection between energy and mv² was first developed in the 1600-1700s by Gottfried Leibniz and Johann Bernoulli, who described it as the "living force." William Gravesande tested this by dropping weights from different heights into a block of clay, discovering a proportionality between penetration depth and impact velocity squared. However, William Thomson is credited for devising the term "kinetic energy" in the mid-1800s.
See also
Potential Energy
Rest Mass Energy
Translational, Rotational and Vibrational Energy
Further reading
Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 9
External links
http://www.physicsclassroom.com/class/energy/Lesson-1/Kinetic-Energy
https://en.wikipedia.org/wiki/Kinetic_energy
http://hyperphysics.phy-astr.gsu.edu/hbase/ke.html
http://www.livescience.com/46278-kinetic-energy.html
https://www.khanacademy.org/science/physics/work-and-energy/work-and-energy-tutorial/a/what-is-kinetic-energy
References
Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 9
http://www.physicsclassroom.com/class/energy/Lesson-1/Kinetic-Energy
https://en.wikipedia.org/wiki/Kinetic_energy
https://courses.lumenlearning.com/physics/chapter/28-6-relativistic-energy/