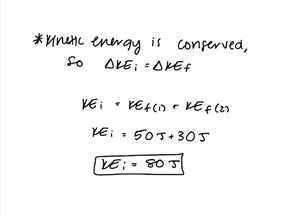The Energy Principle

Claimed by Karen Liu (Fall '24)

The Energy Principle
The basis of the energy principle can be described with the statement, "energy can neither be created nor destroyed." Thus, energy may only flow from one system to its surroundings. The observable universe is comprised of this system and everything else not in the system called the surroundings. The energy principle is used to describe changes in energy on a system. These energies can take numerous different forms including Kinetic Energy, Potential Energy, Chemical Energy, Rest Energy, and Thermal Energy. Creating boundaries allows for the conservation of these different types energy in that energy is not lost nor is it gained, it is simply transferred into other forms. Any energy moving over the boundaries therefore can be accounted for having been transferred from a system to its surroundings and vice versa. This notion is the core idea informing the Energy Principle: The change in energy of the system should be equal to the energy inputs from surroundings.

The Main Idea

The Energy Principle, also referred to as The First Law of Thermodynamics, defines the transfer of energy between systems. It is defined with the fact that the change of the energy of system is equal to the work surrounding in addition to heat transfers from the surroundings as well. This principle can be modeled by the equations:

(1) ΔE = Q+W
(2) ΔE_system + ΔE _surroundings = 0

You can see that these equations (particularly equation 2) describe Conservation of Energy, which is a main idea in physics, particularly in this course!

How will we use the energy principal?

In this course, we can apply the Energy Principal to many different scenarios. We can track how energy takes on different forms during an event. Whether its potential energy being turned into kinetic energy when a woman goes bungee jumping, or electrical energy turning into heat as you use your laptop, the transformation of energy can tell us a lot about a given scenario.

A basic outline for how to solve a problem using the energy principal:

(1) Identify the system and surroundings
(2) Identify the initial state and the final state of the system
(3) Determine the different types of energy associated with the problem
(4) Determine if there are values for Q and W (heat and work) associated with the problem
(5) Determine the equations for each type of energy identified
(6) Plug these into the energy equation and solve for the unknowns

Don’t worry if you’re not sure how these steps are worked out yet – you will soon!

Key Note: Beware of double counting!

If you consider a force to be part of the system, its effects contribute to the system's internal energy, such as changes in potential energy or kinetic energy. If you consider it to be in the surroundings, it acts as an external force that does work on the system. The key point is that a force cannot simultaneously be both internal and external – it must be categorized as one or the other to avoid double counting.
Example: If you account for the work done by gravity on a falling object and also include the gravitational potential energy change without recognizing they're equivalent, you are double counting.

Single Particle vs Multi Particle Systems

As with many concepts in physics, calculating the energy for the multi particle system is exactly the same as calculating the energy for a single particle system – except for the fact that you will need to account for multiple particles.

For example, If a system of one particle has a kinetic energy of 100J, then the total kinetic energy for that system is 100J. If another system consists of three particles, each with a kinetic energy of 20J, then the total kinetic energy of this system is 60J.

The same idea applies for gravitational potential energy, electric potential energy, etc.

Here is that same concept in another form:

KE_final + U_final = Work_surr + Q + KE_intial + U_initial

For a multi-particle system: E_system=(K₁+K₂+K₃+…)+(U_1,2+U_1,3+U_2,3+…)

Click here for a demonstration of the Energy Principle

Mathematical Models

These are the main equations you will be using to solve problems using the Energy Principal. For each problem given, you will only have to pick and choose which equations are necessary based on the types of energy you identify in the system. More more in depth explanations of each type of energy, click on the links in the "See also' section below.

The Energy Principle
[math]\displaystyle{ {∆E} = {Q + W} }[/math] where [math]\displaystyle{ {Q} }[/math] is heat and [math]\displaystyle{ {W} }[/math] is the amount of work acting on the system.

[math]\displaystyle{ {∆E} = {∆K + ∆E_{Rest} + ∆U + ∆E_{Thermal}} }[/math] - the different types of energy that can be associated with a given particle in a system. Not all have to be present. These terms will vary based on the internal properties of the system being observed.

Rest Mass Energy
Rest mass energy is the energy inherent in an object due to its mass, even when it is not in motion. This energy will only change if the system we are studying subatomic particles, nuclear reactions like nuclear fission or fusion, or if we are dealing with relativistic systems.

The formula for rest mass energy, derived from Einstein's theory of relativity, is:

[math]\displaystyle{ E_{rest} = m c^2 }[/math]

where:

[math]\displaystyle{ E_{rest} }[/math] is the rest mass energy (in joules, J),
m is the rest mass of the object (in kilograms, kg),
c is the speed of light in a vacuum (approximately [math]\displaystyle{ 3 \times 10^8 }[/math] meters per second).

Kinetic Energy

Translational kinetic energy is the energy of motion for an object moving in a straight line or along a trajectory.

The formula for basic kinetic energy (translational kinetic energy) is:

[math]\displaystyle{ KE = \frac{1}{2} m v^2 }[/math]

where:

KE is the kinetic energy (in joules, J),
m is the mass of the object (in kilograms, kg),
v is the velocity of the object (in meters per second, m/s).

Rotational kinetic energy is the energy of motion for a rotating object. We use this when an object is rotating. We can also combine rotational kinetic energy with translational kinetic energy when the object both translates and rotates.

The formula for rotational kinetic energy is:

[math]\displaystyle{ KE_{\text{rot}} = \frac{1}{2} I \omega^2 }[/math]

where:

KE_rot is the rotational kinetic energy (in joules, J),
I is the moment of inertia (in kg·m²),
ω is the angular velocity (in radians per second, rad/s).

Thermal Energy

Thermal energy is the energy associated with the temperature of the system, and is the internal energy of a system due to the random motion of its particles.

The formula for the thermal energy change is:

[math]\displaystyle{ \Delta E_{thermal} = mc\Delta T }[/math]

where:

[math]\displaystyle{ \Delta E_{thermal} }[/math] is the thermal energy or heat transfer (in joules, J),
m is the mass of the substance (in grams, g),
c is the specific heat capacity of the substance (in joules per kilogram per degree Celsius, J/(kg·°C)),
ΔT is the change in temperature (in degrees Celsius or Kelvin, °C or K).

Gravitational Potential Energy
The formula for gravitational potential energy near the surface of the earth is:

[math]\displaystyle{ U_{grav} = m g h }[/math]

where:

[math]\displaystyle{ U_{grav} }[/math] is the gravitational potential energy (in joules, J),
m is the mass of the object (in kilograms, kg),
g is the acceleration due to gravity (approximately 9.81 m/s² on Earth),
h is the height of the object above a reference point (in meters, m).

The formula for gravitational potential for universal gravitation is:

[math]\displaystyle{ U_{\text{grav}} = - G \frac{m_1 m_2}{| \vec{r} |} }[/math]

where:

[math]\displaystyle{ U_{\text{grav}} }[/math] is the gravitational potential energy (in joules, J),
[math]\displaystyle{ G }[/math] is the gravitational constant ([math]\displaystyle{ G \approx 6.674 \times 10^{-11} \, \text{N·m}^2/\text{kg}^2 }[/math]),
[math]\displaystyle{ m_1 }[/math] is the mass of the first object (in kilograms, kg),
[math]\displaystyle{ m_2 }[/math] is the mass of the second object (in kilograms, kg),
[math]\displaystyle{ \vec{r} }[/math] is the position vector between the two masses; [math]\displaystyle{ |\vec{r}| }[/math] is the magnitude of the position vector (the distance between the two objects, in meters, m).

Spring Potential Energy
The formula for spring potential energy is:

[math]\displaystyle{ U_{spring} = \frac{1}{2} k_s s^2 }[/math]

where:

[math]\displaystyle{ U_{spring} }[/math] is the spring potential energy (in joules, J),
[math]\displaystyle{ k_s }[/math] is the spring constant (in newtons per meter, N/m),
s is the displacement from the spring's equilibrium position (in meters, m).

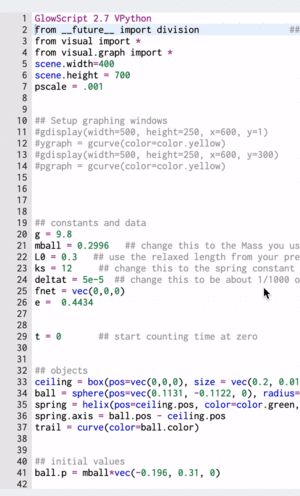
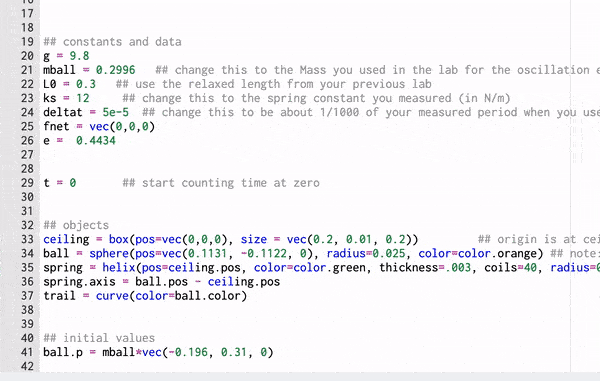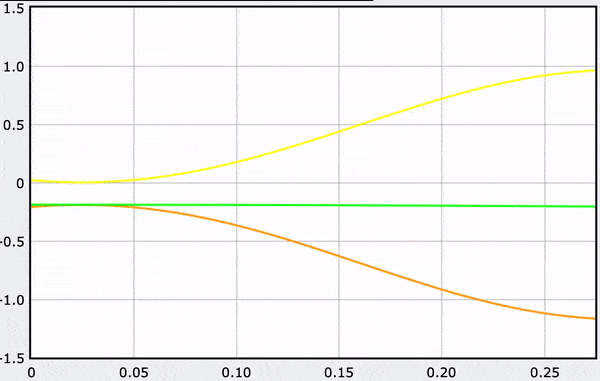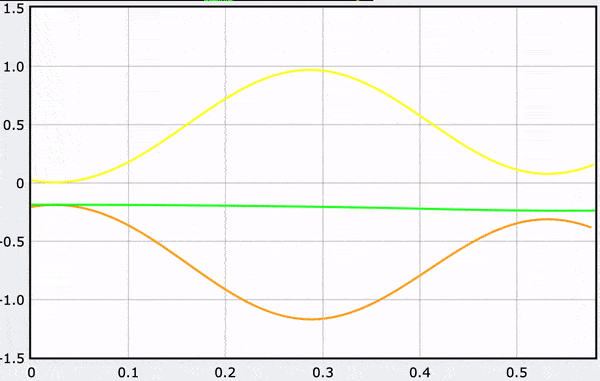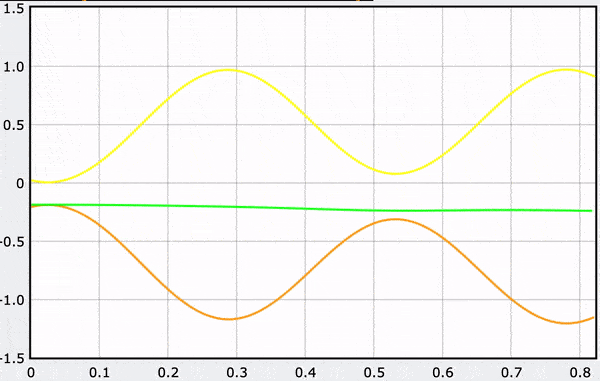
A Computational Model

These gifs demonstrate the energy principal from a Conservation of Energy standpoint. As the ball on a spring approaches the equilibrium point, the kinetic energy increases and the spring potential decreases. These values will oscillate, but the total energy will stay constant! This demonstration was written in GlowScript and iteratively updates the ball's momentum while taking into account the spring force.

Examples

Simple

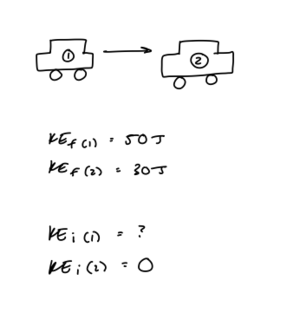
Car Crash:

Two cars are in a parking lot. The first car crashes into the second car, which is initially at rest. The final kinetic energy of the first car is 50J and the final kinetic energy of the second car is 30J. What is the initial kinetic energy of the system?

Step 1: Draw the problem and write out what you know

Step 2: Apply the Energy Principle

Remember - Kinetic energy is a scalar, not a vector - express your answer as such!

Middling

A ball of mass m = 3 kg is kicked off the edge of a cliff from an initial height of h = 10 m above the ground. The ball's initial velocity is <5, 0, 0> m/s. After some time, the ball lands flat on the ground at a horizontal distance of d = 7.14 m from the base of the cliff.

What is the speed of the ball when it hits the ground?

Step One: Identify the system and surroundings, write out the variables you know, and the one you are trying to solve.

system: box + Earth

surroundings: nothing

initial:

[math]\displaystyle{ y_i = h = 10 m }[/math]
[math]\displaystyle{ v_i = 5 m/s }[/math]

final:

[math]\displaystyle{ y_f = 0 }[/math]
[math]\displaystyle{ v_f = ?? }[/math]

Step Two: Apply the Energy Principle

[math]\displaystyle{ \Delta E = W + Q }[/math]

[math]\displaystyle{ \Delta K + \Delta U_g = 0 }[/math]

[math]\displaystyle{ \frac{1}{2} m (v_f^2 - v_i^2) + mg (y_f - y_i) = 0 }[/math]

[math]\displaystyle{ \frac{1}{2} (v_f^2 - v_i^2) - gh = 0 }[/math]

[math]\displaystyle{ \frac{1}{2} (v_f^2 - v_i^2) = gh }[/math]

[math]\displaystyle{ v_f^2 - v_i^2 = 2gh }[/math]

[math]\displaystyle{ v_f^2 = 2gh + v_i^2 }[/math]

[math]\displaystyle{ v_f = \sqrt{2gh + v_i^2} = \sqrt{(2)(9.8)(10) + 5^2} }[/math]

[math]\displaystyle{ v_f = 14.9 m/s }[/math]

Difficult

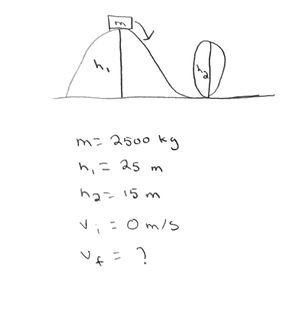
A rollercoaster with passengers has a mass of 2500kg. The rollercoaster is powered to the top of a 25m hill where it pauses for a moment at rest. It then plunges down the hill to ground level where it enters a 15m high vertical loop.

What is the speed of the rollercoaster at the top of the vertical loop?

Step One: Draw the problem out, write out the variables you know, and the one you are trying to solve.

Step 2: Apply the Energy Principle

Difficult

A horizontal spring with stiffness k = 20 N/m and relaxed length [math]\displaystyle{ L_0 }[/math] = 5 m is fixed to a wall and attached to a block of mass m = 8 kg on the other end (no friction between the block and the table). Right now, the spring is compressed to a length of L = 2.5 m, and the block moves to the left with an initial speed of 3 m/s.

How fast will the block move when the spring is relaxed?

Step One: Identify the system and surroundings, write out the variables you know, and the one you are trying to solve.

System: box + spring

Surroundings: nothing (technically, the earth + table are in the surroundings, but since they are vertical forces and the motion is horizontal, the force and displacement are perpendicular, meaning W = 0)

Initial:

[math]\displaystyle{ v_i = 3 m/s }[/math]
[math]\displaystyle{ s_i = 2.5 - 5 = -2.5 m }[/math]

Final:

[math]\displaystyle{ v_f = ?? }[/math]
[math]\displaystyle{ s_f = 0 }[/math]

Step Two: Apply the Energy Principle

[math]\displaystyle{ \Delta E = W + Q }[/math]

[math]\displaystyle{ \Delta K + \Delta U_s = 0 }[/math]

[math]\displaystyle{ \frac{1}{2} m (v_f^2 - v_i^2) + \frac{1}{2} k (s_f^2 - s_i^2) = 0 }[/math]

since [math]\displaystyle{ s_f }[/math] = 0 we can get rid of [math]\displaystyle{ s_f^2 }[/math]

[math]\displaystyle{ \frac{1}{2} m (v_f^2 - v_i^2) = \frac{1}{2} ks_i^2 }[/math]

We can cancel out the [math]\displaystyle{ \frac{1}{2} }[/math] on both sides of the equation

[math]\displaystyle{ m (v_f^2 - v_i^2) = ks_i^2 }[/math]

Solve for [math]\displaystyle{ v_f }[/math]

[math]\displaystyle{ v_f = \sqrt{\frac{ks_i^2}{m} + v_i^2} = \sqrt{\frac{(20)(-2.5)^2}{8} + 3^2} }[/math]

[math]\displaystyle{ v_f = 4.96 m/s }[/math]

Connectedness

One of the best ways to illustrate the Energy Principle in the real world is to imagine someone holding the ball over the top of a building. Since the person is holding the ball, the ball is not moving and has 0J of kinetic energy, however, since the ball is at its highest point, it will have its greatest potential energy because of U = mgh. Once the ball is released, the ball's velocity starts to speed up under the force of gravity, thus increasing kinetic energy. At the same time, the height of the ball is decreasing, and so is potential energy. The relationship between these, in fact, is inverse: as the value of one decreases, that of the other increases in exact proportion. Right before the ball hits the ground, its potential energy will be near zero, and its kinetic energy will be at its highest.

History

The concept of energy and its connection to the amount of work performed goes all the way back to the age of steam engines; physicists and engineers came up with this notion to determine the mechanical and thermal efficiency of their machines. In the 1850's, people like William Thomson and William Rankine began to come up with terms like 'kinetic energy' and 'potential energy' to model the different types of observed forces. After the 1920's, this study of science became to be known as thermodynamics, the science of energy transformations. This led to the laws of thermodynamics, one of which relates to the conservation of energy. William Rankine was the first to discuss the law of the conservation of energy in relation to a more general "energy principle". His discussions and work in this field defined the relationships between energy that we now consider the Energy Principle.

The Energy Principle

Contents

The Main Idea

How will we use the energy principal?

Single Particle vs Multi Particle Systems

Mathematical Models

A Computational Model

Examples

Simple

Middling

Difficult

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu