Gravitational Potential Energy

Claimed by: Dhruv Saxena (Spring 2023)

Main Idea

Gravitational Potential Energy ([math]\displaystyle{ U_{grav} }[/math]) is the energy stored in an object as a result of its position in a gravitational field and attractive forces from surrounding objects. The general case of gravitational potential energy, when two objects with mass are attracted to each other, depends on the distance between the two and masses of each. The total gravitational energy [math]\displaystyle{ U_{grav} }[/math] is inversely proportional to the distance between the two objects with mass. In other words, the closer together together two things are, the greater the magnitude of gravitational potential energy [math]\displaystyle{ |U_{grav}| }[/math] will be. Additionally, the total gravitational potential energy [math]\displaystyle{ U_{grav} }[/math] is directly proportional to the masses of the objects. When the objects are more massive, the magnitude [math]\displaystyle{ |U_{grav}| }[/math] will be greater.

Gravitational Potential Energy, as implied by the name, is a form of potential energy. Potential energy is energy that is stored in an object due to its position or chemical properties that can be translated into kinetic or thermal energy. In these terms it clarifies how an object in space has gravitational potential energy and as it loses this potential energy while falling to the ground, it gains speed, or kinetic energy.

An important note is also that gravitational potential energy is negative. This results due to the integration determining gravitational potential energy but an intuitive way to understand this is that the negative sign indicates that when masses approach each other in a gravitational field gravity is doing positive work. If that didn't make sense, remember the idea that kinetic energy is always positive so when [math]\displaystyle{ K }[/math] increases if we want to keep [math]\displaystyle{ E_{total} }[/math] the same, [math]\displaystyle{ U_{grav} }[/math] must be negative.

An important aspect to acknowledge about Gravitational potential energy is that it must be looked at in the difference between two points. An example that showcases this is the difference in gravitational potential energy between a rock on the surface of the earth and a rock in space. While the rock in space has a smaller magnitude of potential energy in comparison to the rock on the surface, the change in energy from space to the ground is greater than the energy the rock on the ground has in respect to ground level. This is why the rock in space will gain speed and energy as it falls through the air towards the ground.

We commonly use gravitational potential energy when we're trying to determine the work required to life an object with mass [math]\displaystyle{ m }[/math] to a height a [math]\displaystyle{ h }[/math]. Since the gravitational potential energy for objects near the surface of the Earth (As we will derive in the Mathematical Model section) can be represented as [math]\displaystyle{ U_{grav} = mgh }[/math] we can intuitively see that the force due to gravity on an object of mass [math]\displaystyle{ m }[/math] would be [math]\displaystyle{ mg }[/math] and the height we'd be lifting it to would be [math]\displaystyle{ h }[/math]. Since work [math]\displaystyle{ W = \vec F \cdot \vec d }[/math] we see a parallel idea between [math]\displaystyle{ U_{grav} }[/math] and [math]\displaystyle{ W }[/math].

Checkout this video for a quick review and explanation.

Mathematical Model

General Form for Gravitational Potential Energy:

[math]\displaystyle{ U_{grav} = -G\frac{m_1 m_2}{r} }[/math]

[math]\displaystyle{ U_{grav} }[/math] is the total gravitational potential energy. Like other energy it is measured in Joules ([math]\displaystyle{ J }[/math]).
[math]\displaystyle{ m_1 }[/math] is the mass of the first object you are measuring [math]\displaystyle{ U_{grav} }[/math] between. The standard unit for mass is kilograms ([math]\displaystyle{ kg }[/math]).
[math]\displaystyle{ m_2 }[/math] is the mass of the second object you are measuring [math]\displaystyle{ U_{grav} }[/math] between. The standard unit for mass is kilograms ([math]\displaystyle{ kg }[/math]).
[math]\displaystyle{ r }[/math] is the distance between the center of mass [math]\displaystyle{ cm }[/math] of both masses [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2 }[/math]. (If you don't know how to find center of mass yet, you can probably assume that its the center of whatever mass you're using). The standard unit for distance is meters ([math]\displaystyle{ m }[/math]).
[math]\displaystyle{ G }[/math] is the gravitational constant or [math]\displaystyle{ 6.67408 \times 10^{-11} \frac{m^3}{kg \times s^2} }[/math]

We can make some simplifying approximations (similar to what we did with gravitational force) when we are trying to measure gravitational potential energy due to the Earth near the surface of the Earth.

Gravitational Potential Energy near the Earth's surface:

[math]\displaystyle{ U_{grav} = mgh }[/math]

[math]\displaystyle{ U_{grav} }[/math] is the total gravitational potential energy. Like other energy it is measured in Joules ([math]\displaystyle{ J }[/math]).
[math]\displaystyle{ m }[/math] is the mass of the object you are measuring [math]\displaystyle{ U_{grav} }[/math] of. The standard unit for mass is kilograms ([math]\displaystyle{ kg }[/math]).
[math]\displaystyle{ h }[/math] is the height above the Earth's surface that the object is (make sure that it is near the Earth's surface. A good rule of thumb is that it really shouldn't be in space :-) ). The standard unit for height is meters ([math]\displaystyle{ m }[/math]).

Gravitational Potential Energy Relation to Gravitational Force:

Potential energy is always the integral of the force over the distance the force is applied.
We can observe how the gravitational potential energy comes about by looking at the gravitational force

[math]\displaystyle{ U_{grav} = \int_{-\infty}^{r} F_g dr }[/math]

[math]\displaystyle{ Fg = -G\frac{m_1 m_2}{r^2} }[/math]

[math]\displaystyle{ U_{grav} = \int_{-\infty}^{r} -G\frac{m_1 m_2}{r^2} dr = -G\frac{m_1 m_2}{r} }[/math]

Computational Model

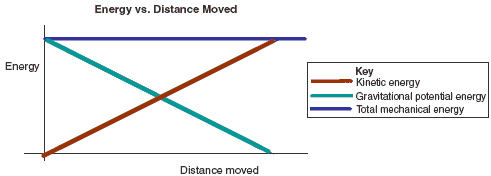
In order to understand gravitational potential energy in a computational manner, we must be able to represent it in some way which we can visually understand it. To do this, we will use an energy graph. An energy graph is a graph which plots potential energy, kinetic energy, and total energy. There are a few easy steps to follow when making an energy graph.

Draw [math]\displaystyle{ U_{grav} }[/math] vs [math]\displaystyle{ |\vec r| }[/math] for the interaction ([math]\displaystyle{ |\vec r| }[/math] is the distance the object is from what it's attracted to)
At some distance [math]\displaystyle{ |\vec r| }[/math] where [math]\displaystyle{ K }[/math] is known, plot the point [math]\displaystyle{ (|\vec r|, K) }[/math]
Add the known value of [math]\displaystyle{ K }[/math] to the value of [math]\displaystyle{ U }[/math] at that same separation [math]\displaystyle{ |\vec r| }[/math]
Plot the horizontal line [math]\displaystyle{ K+U }[/math] across the graph
Calculate the rest of [math]\displaystyle{ K }[/math] knowing that [math]\displaystyle{ K+U }[/math] = the same constant
Plot the values

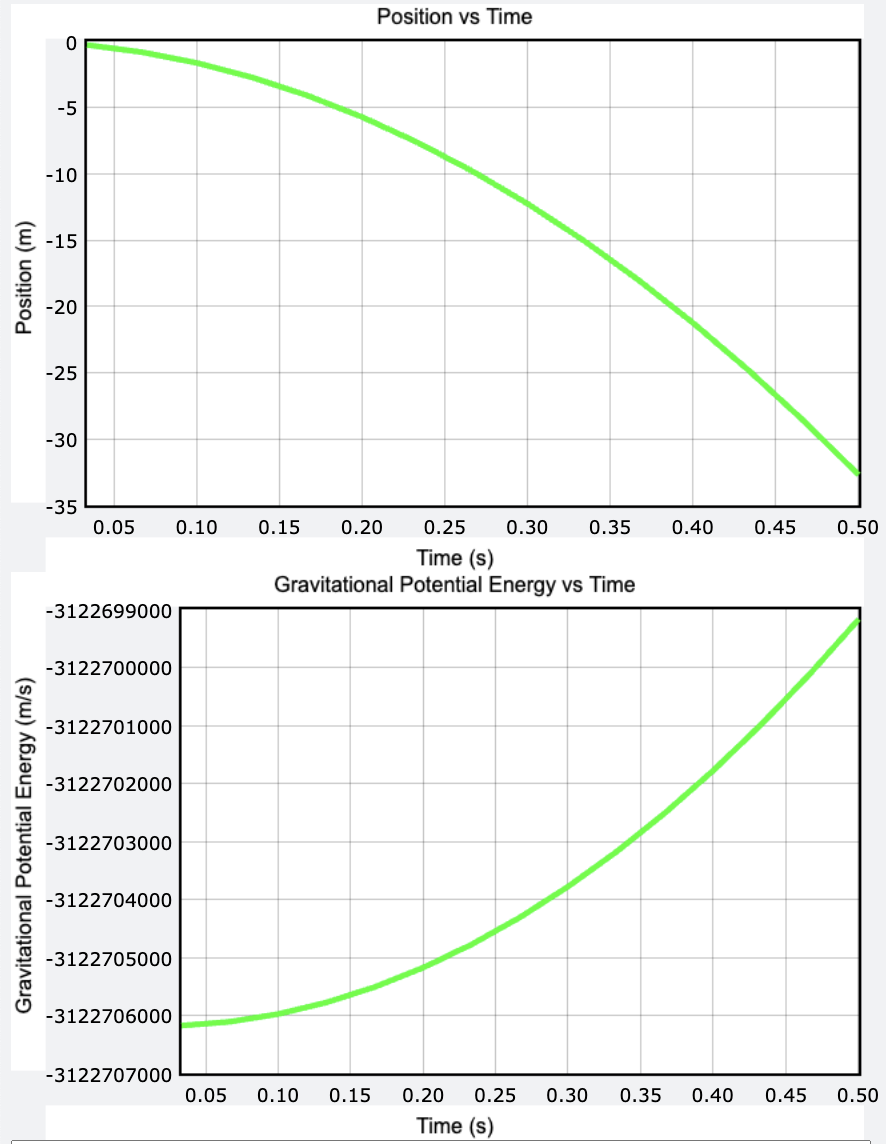
From https://www.glowscript.org/#/user/Dhruv3745/folder/MyPrograms/program/lab2

The above graph shows an example of what an energy versus distance graph may look like. We can see that as the distance increases, [math]\displaystyle{ U_{grav} }[/math] decreases and [math]\displaystyle{ K }[/math] increases.

VPython Examples

Suppose that we have a spaceship that is passing close to the Earth. We can computationally model the gravitational potential energy of this spaceship and visually represent it using energy graphs. The basic structure of our program will follow what is usually done for VPython programs:

Pick a delta t
Initialize our variables
while our time < time bound do
	Calculate new values for our variables
	Update how they are presented
	increment our time + delta t

Create/Initialize the Energy Graphs

trail = curve(color=craft.color)		#This creates a trail for the spacecraft
U_graph = gcurve(color=color.blue) 		#A plot of the Potential energy
K_graph = gcurve(color=color.yellow) 	#A plot of the Kinetic energy
Energy_graph = gcurve(color=color.green)#A plot of the Total energy

Calculate and Update the variables in our Loop

K_craft = 0.5*mcraft*mag2(pcraft/mcraft)	#Kinetic Energy using equation: .5mv^2
U_craft_Earth = -G*mcraft*mEarth/mag(craft.pos-Earth.pos) #Craft + Earth interaction energy
E = K_craft + U_craft_Earth		#Approximate Total energy

Update our graphs

U_graph.plot(pos=(t,U_craft_Earth))		#Potential energy as a function of time
K_graph.plot(pos=(t,K_craft))			#Kinetic energy as a function of time
Energy_graph.plot(pos=(t,E))			#Total energy as a function of time

Here is what a slightly more complex product would like like (this example has the moon's gravity incident on the spaceship as well):

Click here to see it in action if you can't see it below.

Guide on Solving Problems

The Law of Conservation of energy states that energy is neither created nor destroyed. This means that a system's energy is always the same at any point in time as long as it is not acted upon by an external influence.

[math]\displaystyle{ E_i = E_f }[/math]

[math]\displaystyle{ U_{g_{init}} + K_{init} = U_{g_{final}} + K_{final} }[/math]

Upon seeing any problem, you need to calculate the energy it would have at the final/initial state (depending on what information is given). Isolate the unknown and solve.

Examples

Simple

Question:

A ball of mass [math]\displaystyle{ 100 }[/math] grams is [math]\displaystyle{ 7 }[/math] m above the ground, initially at rest ([math]\displaystyle{ K_i = 0 }[/math]). When the ball is [math]\displaystyle{ 4 }[/math] m above the ground what is the kinetic energy ([math]\displaystyle{ K_f }[/math])? Choose the ball + Earth system.

Hint: Try drawing a picture of the situation. What has changed between the ball being at a higher height versus a lower height? Specifically how does this relate to the balance of potential energy and kinetic energy?

Solution:

Start from the energy principle:

[math]\displaystyle{ K_i + U_i = K_f + U_f }[/math]

Since the ball starts from rest we know that [math]\displaystyle{ K_i = 0 }[/math]. Since the ball is also [math]\displaystyle{ 7 }[/math] meters above the ground we know that there will be some potential energy due to gravity. We can use the equation above for an estimate of gravitational potential energy for an object close to the Earth's surface: [math]\displaystyle{ mgh }[/math]. Therefore, we now know:

[math]\displaystyle{ 0 + mgh_i = K_f + U_f }[/math]

where [math]\displaystyle{ h_i }[/math] is the initial height of the ball. Since the ball doesn't fall all the way to the ground in its final state (It's still [math]\displaystyle{ 4 }[/math] m above the ground) we know that there will still be some potential energy due to gravity.

[math]\displaystyle{ mgh_i = K_f + mgh_f }[/math]

We can then isolate [math]\displaystyle{ K_f }[/math] with some subtraction

[math]\displaystyle{ K_f = mg(h_i - h_f) }[/math]

If we know substitute the numbers that we know into the equation we get that

[math]\displaystyle{ K_f = .1 \cdot 9.8 \cdot (7 - 4) = 2.94 }[/math] Joules

Medium

Question:

In February 2013 a large meteor, whose mass has been estimated to be [math]\displaystyle{ 1.2 \times 10^7 kg }[/math], fell to Earth near Chelyabinsk, Russia. (This meteor exploded spectacularly at height of about [math]\displaystyle{ 30 }[/math] km, doing significant damage to objects on the ground.) Consider a meteor of the same mass falling toward the Earth. Choose the Earth plus the meteor as the system. As the meteor falls from a distance of [math]\displaystyle{ 1 \times 10^8 }[/math] m from the center of the Earth to [math]\displaystyle{ 1 \times 10^7 }[/math] m, what is the change in the kinetic energy of the meteor? The mass of the Earth is about [math]\displaystyle{ 6 \times 10^{24}kg }[/math].

Hint: Consider how far the meteor is from Earth. Would it be considered an object near the surface of Earth or would we have to use the other model of gravitational potential energy? What is the quantity that we're solving for?

Solution:

Start with the energy principle:

[math]\displaystyle{ K_i + U_i = K_f + U_f }[/math]

Perhaps a better organization of this equation, keeping in mind that we are solving for the change in kinetic energy would be as follows:

[math]\displaystyle{ K_i - K_f = U_f - U_i }[/math]

And if we want to put it in terms of changes

[math]\displaystyle{ - (K_f - K_i) = U_f - U_i }[/math]

[math]\displaystyle{ - \Delta K = \Delta U }[/math]

We can now utilize the fact that we know both the initial and final height of the meteor in relation to the Earth. Since the meteor is not quite near the Earth's surface, we will use the formula for gravitational potential energy that does not make that assumption.

We know that:

[math]\displaystyle{ \Delta U = U_f - U_i }[/math]

Which if we substitute in the gravitational potential energy equations would be:

[math]\displaystyle{ \Delta U = -G\frac{m_1 m_2}{r_f} - -G\frac{m_1 m_2}{r_i} = -G\frac{m_1 m_2}{r_f} + G\frac{m_1 m_2}{r_i} }[/math]

We can then substitute in the values that we are given in the problem to solve for potential energy.

[math]\displaystyle{ - 6.67408 \times 10^{-11} \frac{(6\times 10^{24})(1.2 \times 10^7)}{1\times 10^7} + 6.67408 \times 10^{-11}\frac{(6\times 10^{24})(1.2 \times 10^7)}{1\times 10^8} = \Delta U }[/math]

[math]\displaystyle{ \Delta U = -4.32216 \times 10^{14}J }[/math]

We can then use this value to solve for the change in kinetic energy using our earlier derived equation which says that:

[math]\displaystyle{ -\Delta K = \Delta U }[/math]

[math]\displaystyle{ - \Delta K = -4.32216 \times 10^{14}J }[/math]

[math]\displaystyle{ \Delta K = 4.32216 \times 10^{14}J }[/math]

Hard

Question:

A robot spacecraft lands on an asteroid, picks up a sample, and blasts off to return to the Earth; it's total mass is [math]\displaystyle{ 1500 }[/math] kg. When it is [math]\displaystyle{ 200 }[/math] km from the center of mass of the asteroid, its speed is [math]\displaystyle{ 5.0 \frac{m}{s} }[/math], and the rockets are turned off. At the moment when it has coasted to a distance [math]\displaystyle{ 500 }[/math] km from the center of the asteroid, its speed has a decreased to [math]\displaystyle{ 4.1 }[/math] m/s. Calculate the mass of the asteroid.

Hint: Do you see any chance of a variable cancelling out once you start working with your algebra?

Solution:

Start with the energy principle as always:

[math]\displaystyle{ K_i + U_i = K_f + U_f }[/math]

We know that the beginning and end of its journey both has kinetic energy as well as potential energy due to the gravitational potential energy between the spaceship and the asteroid. Knowing this, and taking it into account, we can rewrite our energy principle with slightly more specific terms.

[math]\displaystyle{ \frac{1}{2}m_{ship}v_i^2 - G\frac{m_{ship} m_{asteroid}}{r_i} = \frac{1}{2}m_{ship}v_f^2 - G\frac{m_{ship} m_{asteroid}}{r_f} }[/math]

If we then factor out the [math]\displaystyle{ m_{ship} }[/math] we might see a relation that is helpful.

[math]\displaystyle{ m_{ship}(\frac{1}{2}v_i^2 - G\frac{m_{asteroid}}{r_i}) = m_{ship}(\frac{1}{2}v_f^2 - G\frac{m_{asteroid}}{r_f}) }[/math]

We can divide both sides of the equation by [math]\displaystyle{ m_{ship} }[/math].

[math]\displaystyle{ \frac{1}{2}v_i^2 - G\frac{m_{asteroid}}{r_i} =\frac{1}{2}v_f^2 - G\frac{m_{asteroid}}{r_f} }[/math]

We can now isolate the [math]\displaystyle{ m_{asteroid} }[/math] with a little bit more algebra.

[math]\displaystyle{ \frac{1}{2}v_i^2 - \frac{1}{2}v_f^2 = G\frac{m_{asteroid}}{r_i} - G\frac{m_{asteroid}}{r_f} }[/math]

[math]\displaystyle{ \frac{1}{2}v_i^2 - \frac{1}{2}v_f^2 = m_{asteroid}(G\frac{1}{r_i} - G\frac{1}{r_f}) }[/math]

[math]\displaystyle{ m_{asteroid} = \frac{\frac{1}{2}(v_i^2 - v_f^2)}{G(\frac{1}{r_i} - \frac{1}{r_f})} }[/math]

We can then substitute in the values given to us in the problem to determine what the mass of the asteroid was.

[math]\displaystyle{ m_{asteroid} = \frac{\frac{1}{2}((5)^2 -(4.1)^2)}{G(\frac{1}{200} - \frac{1}{500})} }[/math]

Which gives us our final answer of:

[math]\displaystyle{ m_{asteroid} = 2.04648 \times 10^{13}kg }[/math]

Connectedness

Gravitational potential energy can be related to industrial engineering for someone who chooses to work in a manufacturing or aerospace. It is also very important to include when determining the escape velocity and other forces necessary for rockets, probes, and satellites to travel within space. It, also, has some importance in animation and game development as it is an essential part of physics engines and, without a doubt, one of the most obvious interactions visible in society.

History

Galileo Galilei and Isaac Newton discovered how forces are related to acceleration. Newton summed up this information with his Laws of Motion. Mechanical energy was discovered by analyzing the equations derived from Newton's Laws. It was later realized that when two objects interact they exert forces on each other and that work ([math]\displaystyle{ W = \vec F \cdot \vec d }[/math] ) must be replaced with potential energy in a system of interacting objects within a gravitational field.

The idea of gravitational potential energy specifically was introduced by Johann Bernoulli in 1738. The concept was later taken up by several people in several different ways. For example Euler, Lagrange, Laplace and Legendre looked at gravity as it revolved around something while Newton focused on gravitational attraction if the object is a sphere. Euler and Co later confirmed the shape does not matter for the object.

http://www.physicsclassroom.com/class/energy/Lesson-1/Potential-Energy

http://hyperphysics.phy-astr.gsu.edu/hbase/gpot.html

http://weelookang.blogspot.com/2010/10/ejs-open-source-gravity-field-model.html

Gravitational Potential Energy

Contents

Main Idea

Mathematical Model

General Form for Gravitational Potential Energy:

Gravitational Potential Energy near the Earth's surface:

Gravitational Potential Energy Relation to Gravitational Force:

Computational Model

VPython Examples

Guide on Solving Problems

Examples

Simple

Medium

Hard

Connectedness

History

See also

Further reading

External links

References

Navigation menu