Curving Motion
Charity Tarver Fall 2023
Main Idea
In the previous section, we introduced the idea of conservation of momentum. By choosing multiple particles as the system, we can assume that the forces exerted by the particles in the system are reciprocal of one another, based on Newton's Third Law of Motion. The total change in momentum is zero if the system's forces all canceled out and no forces in the surrounding are acting on the system. This special case, where the momentum of the system remains constant ([math]\displaystyle{ \Delta p = 0 }[/math]), can be implicated in many situations that helps us to identify forces exerted on the system. However, in the case when the momentum of the system changes with time, which means velocity and/or direction of motion are nonconstant and additional terms are needed to define the magnitude and direction of the momentum of the objects in the system. The momentum of an object is nonconstant when it is traveling along a curved path, regardless of whether or not it's speed along the curve is changing because the direction also changes. Curving motion can be analyzed using the properties of the parallel and perpendicular components of net Force ([math]\displaystyle{ F_{net} }[/math]) as well as understanding the motion's "Kissing Circle".
Mathematical Model
Parallel and Perpendicular Forces
The parallel force lies along the direction of the momentum vectors and is calculated as [math]\displaystyle{ \mathbf{F_{\parallel}} = |\mathbf{F_{net}}| \text{cos}(\theta) \ \mathbf{\hat p} }[/math]. Since [math]\displaystyle{ \mathbf{F_{net}} }[/math] is the sum of its parallel and perpendicular components, [math]\displaystyle{ \mathbf{F_{\perp}} }[/math] can be obtain simply by taking the difference between the two: [math]\displaystyle{ \mathbf{F_{\perp}} = \mathbf{F_{net}} - \mathbf{F_{\parallel}} = \mathbf{F_{net}} - |\mathbf{F_{net}}|\text{cos}(\theta) \ \mathbf{\hat p} }[/math]
The image above describes a particle moving in a clockwise circular motion. Note that [math]\displaystyle{ \mathbf{F_\perp} }[/math] always points inward for a circular path. [math]\displaystyle{ \mathbf{F_\parallel} }[/math] gives the change in magnitude of the object's momentum, and [math]\displaystyle{ \mathbf{F_\perp} }[/math] gives the change in direction of the object's momentum.
Understanding the Components of [math]\displaystyle{ \frac{d\mathbf{p}}{dt} }[/math]
When the change in momentum with respect to time is nonzero, we will consider both the parallel and perpendicular components of momentum, and their relationship to the net force. If an object is speeding up or slowing down, [math]\displaystyle{ \frac{d \mathbf{p}}{dt}_{\parallel} \ne 0 }[/math]. If an objects is turning while traveling along a path, [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_{\perp} \ne 0 }[/math]. The parallel component accounts for the change in speed of the motion, while the perpendicular component accounts for the change in direction of the motion. Here is a list of useful formulas:
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt} = \frac{d\mathbf{p}}{dt}_\parallel + \frac{d\mathbf{p}}{dt}_\perp }[/math]
- [math]\displaystyle{ \mathbf{F_{net}} = \mathbf{F_\parallel} + \mathbf{F_\perp} }[/math]
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} = \mathbf{F_\parallel} }[/math] (Change in magnitude of momentum)
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\perp = \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| = \mathbf{F_\perp} }[/math] (Change in direction of momentum)
- [math]\displaystyle{ \mathbf{F_{net}} = \frac{d\mathbf{p}}{dt} = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} + \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| }[/math]
Perpendicular Component and the Kissing Circle
The perpendicular component of momentum can be evaluated further so that it becomes:
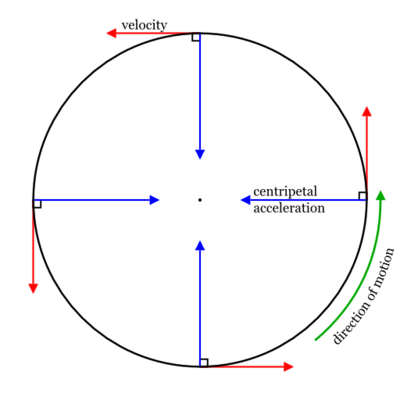
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\perp = \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| = |\mathbf{p}| \frac{|\mathbf{v}|}{R} \mathbf{\hat n} = \frac{mv^2}{R} \mathbf{\hat n} }[/math]
The term [math]\displaystyle{ |\mathbf{p}| \frac{|\mathbf{v}|}{R} \mathbf{\hat n} }[/math] can be understood by drawing an imaginary circle, that touches or 'kisses' some point on a curved path, to represent the instantaneous curvature of an object's trajectory, where [math]\displaystyle{ R }[/math] is the radius of the circle. For a smooth, continuous curving motion, [math]\displaystyle{ \frac{|\mathbf{v}|}{R} }[/math] tells us the degree of which the object is turning and the rate of change of direction,[math]\displaystyle{ \frac{d\mathbf{\hat p}}{dt} }[/math]. The 'Kissing Circle' indicates the direction of the perpendicular component of momentum, which points towards the center of the kissing circle and it's denoted by [math]\displaystyle{ \mathbf{\hat n} }[/math].
Parallel Component and Tangential Properties of Curving Motion
The parallel component of momentum always points in the direction of motion, denoted by [math]\displaystyle{ \mathbf{\hat p} }[/math] and is tangent to the path of motion. The term [math]\displaystyle{ \frac{d|\mathbf{p}|}{dt} }[/math] describes the change in velocity of the objects with respect to time (since [math]\displaystyle{ \mathbf{p} = m\mathbf{v} }[/math]), and it corresponds to the change in the magnitude of the momentum.
There are two scenarios of curving motion that we will entertain here; one where an object is not changing speed along its curved path, and another where the object speeds up or slows down along its curved path. We will start with the constant speed scenario:[math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = 0 }[/math]
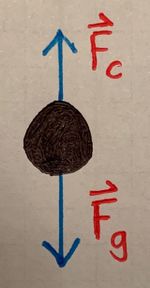
When an object's tangential velocity is constant throughout the entire motion, we can say that the parallel component of [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}} }[/math] is zero, as any change in momentum is solely from altering the direction of the object's momentum as opposed to its magnitude. To understand this in more mathematical terms, the only way the magnitude of a momentum vector can be changed is if some component of the force acting on the object lies in the direction of the objects motion. Otherwise, the net force must be in the perpendicular direction towards the center of the kissing circle, like shown below:
Here we see that the tangential velocities indicated by the red arrows are all of the same magnitude, and the only thing altering them is the centripetal acceleration, which will lead us into our discussion of centripetal and centrifugal forces in the next section. Now we will consider cases where [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel }[/math] is nonzero. In these cases, the speed of the object along its curved path is changing, and our net force vector has a component that is parallel to the object's tangential motion.
Calculating [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel }[/math] and [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\perp }[/math] is possible, given an instantaneous force acting on the object as well as it's initial momentum. We can calculate the final momentum using the Momentum Principle, and then observe any change in magnitude between these two vector quantities. Here, [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\parallel }[/math] is equal to the difference between the magnitudes of the initial and final momentum divided by the change in time. From this, we can calculate [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\perp }[/math] by subtracting [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\parallel }[/math] from the net change in momentum.
Computational Model
The parallel and perpendicular components of [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}} }[/math] can be modeled computationally using VPython. The code below models a situation in which a space craft interacts with the Earth and the Moon.
https://trinket.io/glowscript/f53cc1fa35
In this model, gravitational forces affect the motion of the space craft, causing it to curve in proportion to the perpendicular and parallel components of force. The yellow arrow following the craft's position shows the parallel component of force, and the magenta arrow shows the perpendicular component of force. Aspects of the code that account for these calculations are explained below:
The parallel component of force is calculated from the expression [math]\displaystyle{ {\frac{d|\mathbf{p}|}{dt}} \mathbf{\hat p} }[/math]
p_init = sqrt(pcrafti.x**2+pcrafti.y**2)
p_final = sqrt(pcraft.x**2+pcraft.y**2)
Fnet_tangent = ((p_final-p_init)/deltat)*(pcrafti)/(p_init)
The perpendicular component of force is calculated from the expression [math]\displaystyle{ \mathbf{F_{net}} = \mathbf{F_\parallel} + \mathbf{F_\perp} }[/math].
From this expression, it is seen that [math]\displaystyle{ \mathbf{F_{net}} - \mathbf{F_\parallel} = \mathbf{F_\perp} }[/math]
The computational model uses this insight, and the net force calculated earlier in the code to find the perpendicular component of net force.
Fnet_perp = Fnet - Fnet_tangent
To see the affects of the gravitational force on curving motion, you are encouraged to make changes to the initial values of the code and see the effects on the perpendicular and parallel components of force. These initial values can be edited in the beginning of the code in this section:
CONSTANTS
G = 6.7e-11
mEarth = 6e24
mcraft = 15e3
mMoon = 7
deltat = 60
Fscale = 2e3
pscale = 1e-1
dpscale = 33
OBJECTS AND INITIAL VALUES
Earth = sphere(pos=vector(0,0,0), radius=6.4e6, color=color.cyan)
craft = sphere(pos=vector(-72960000,5248000,0), radius=1e5, color=color.yellow)
vcraft = vector(692,2950,0)
pcraft = mcraft*vcraft
moon = sphere(pos=vector(4e8,0,0), radius = 1.75e6, color=color.white)
moon.v = vector(0,sqrt((G*mEarth)/mag(moon.pos-Earth.pos)),0)
momentum_Moon = mMoon*moon.v
Additionally, here is my supplied computationally simulation model: https://www.glowscript.org/#/user/WolfCTarver/folder/MyPrograms/program/Lab3MyTestSTAR/edit
This is from a prior lab where a star is orbiting a black hole of unknown mass located at the origin. The star has a mass of 2.0e30 kg. The position data (x and y coordinates) of the star will be generated in the starter code, and the resulting trajectory will be unique to me, generated and keyed to my student email by replacing the dummy email address in line 11.
First, we analyze the star's motion to find the net force on the star for all points in the data set using the scaffolded starter code, beginning on line 96. Assume the net force on the star is due solely to a black hole located at the origin and that the time between data points in the trajectory is one day. Using the results of the analysis, we estimate the mass of the black hole.
Then, we launch from the side of the planet that is in the same direction as the planet's motion, but then immediately after takeoff the engines fail! We are now at the mercy of the gravitational forces of the planet and the black hole. The mission is to fly around the black hole (not necessarily orbiting it, but rather getting close to it at some point) without crashing on the planet or the black hole. To do this, we will need to determine what initial velocity your ship must have when it leaves the surface of the planet. We simulate the motion of the spaceship around the planet and black hole, by calculating all the necessary gravitational forces and using Newton's 2nd law to predict the motion of the planet and the spaceship.
Examples
Simple
It's fairly simple identifying cases of curving motion, in which case a person can easily apply [math]\displaystyle{ {\frac{m v^{2}}{R}} }[/math] to a situation immediately. For example, if an object is traveling in a circular path at a constant speed, we can neglect the parallel component of [math]\displaystyle{ \frac{d\mathbf{p}}{dt} }[/math] and [math]\displaystyle{ \mathbf{F_{net}} }[/math], and consider only the perpendicular components, such as tension, gravitational, and contact forces.
Example:
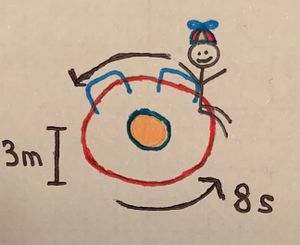
A child whose mass is [math]\displaystyle{ 30 \ \text{kg} }[/math] sits on a merry-go-round at a distance of [math]\displaystyle{ 3 \ \text{meters} }[/math] from the center. The merry-go-round makes one revolution every [math]\displaystyle{ 8 \ \text{seconds} }[/math] and the child moves at a constant speed. What are the magnitude and direction of the net force ([math]\displaystyle{ F_{net} }[/math]) acting on the child?
Solution:
We know that the net force acting on the child is the sum of the perpendicular force ([math]\displaystyle{ F_\perp }[/math]) and the parallel force ([math]\displaystyle{ F_\parallel }[/math]), so it is best to solve for each separately and then add them together.
- Parallel:
- Since the child moves at a constant speed, we know that [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\parallel }[/math] is 0:
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = \mathbf{F_\parallel} = \mathbf{0} }[/math]
- Perpendicular:
- We know that:
- [math]\displaystyle{ |\mathbf{F_\perp}| = {\frac{m v^{2}}{R}} }[/math].
- In this case (no parallel force, and thus circular motion):
- [math]\displaystyle{ v = \frac{\text{Circumference of Circle}}{\text{Period}} = \frac{2 \pi \times R}{T} = \frac{2 \pi \times 3}{8} = 2.36 \ \frac{m}{s} }[/math], where:
- [math]\displaystyle{ R = 3 \ \text{meters} }[/math]
- [math]\displaystyle{ T = 8 \ \text{seconds} }[/math]
- Therefore:
- [math]\displaystyle{ |\mathbf{F_\perp}| }[/math] = [math]\displaystyle{ {\frac{(30)(2.36)^{2}}{3}} = 55.5 \ \text{Newtons} }[/math]
- Net Force:
- [math]\displaystyle{ \mathbf{F_{net}} = \mathbf{F_\parallel} + \mathbf{F_\perp} = 0 + \mathbf{F_\perp} }[/math]
Since [math]\displaystyle{ \mathbf{F_\perp} }[/math] is the only component of the net force, we know that [math]\displaystyle{ |\mathbf{F_{net}}| = 55.5 \ \text{Newtons} }[/math]. This net force is pointing in the perpendicular direction, towards the center of the merry-go-round.
Middling
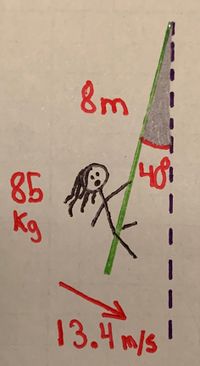
Occasionally, it can be difficult to gauge any components that influence the object's tangential velocity and effectively speed up or slow down the object by altering the magnitude of the momentum vector.
Example:
Tarzan, whose mass is [math]\displaystyle{ 85 \ \text{kg} }[/math], is hanging from a vine that is [math]\displaystyle{ 8 \ \text{meters} }[/math] long. At the instant when he makes a [math]\displaystyle{ 40^\text{o} }[/math] angle between the vine and the vertical, he is traveling at a speed of [math]\displaystyle{ 13.4 \ \frac{m}{s} }[/math].
- a) What is the rate of change of the magnitude of Tarzan's momentum?
- First, we draw a free body diagram for Tarzan:
- We know the magnitude of the change of momentum is related to the net parallel force by: (See Understanding the Components of [math]\displaystyle{ \frac{d\mathbf{p}}{dt} }[/math])
- [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} = \mathbf{F_\parallel} }[/math]
- Taking the magnitude of each part of the equations gives:
- [math]\displaystyle{ \left|\frac{d\mathbf{p}}{dt}_\parallel\right| = \frac{d|\mathbf{p}|}{dt} = |\mathbf{F_\parallel}| }[/math]
- The only force acting in the parallel direction to the momentum of Tarzan is the parallel component of the gravitational force:
- [math]\displaystyle{ |\mathbf{F_\parallel}| = |\mathbf{F_g}| \text{cos}(90^\text{o} - 40^\text{o}) = |\mathbf{F_g}| \text{cos}(50^\text{o}) }[/math]
- The magnitude of the gravitational force is just:
- [math]\displaystyle{ |\mathbf{F_g}| = mg }[/math], where
- [math]\displaystyle{ m = 85 \ \text{kg} }[/math] (Mass of Tarzan)
- [math]\displaystyle{ g = 9.81 \ \frac{m}{s^2} }[/math] (Acceleration due to gravity)
- Therefore:
- [math]\displaystyle{ \frac{d|\mathbf{p}|}{dt} = 85 \times 9.81 \times \text{cos}(50^\text{o}) = 536 \ \frac{\text{kg m}}{\text{s}^2} }[/math]
- b) What is the tension in the vine?
- Finding the tension in the vine can be done in the easiest way by looking at the component of the net force perpendicular to the momentum. We know that: (See Perpendicular Component and the Kissing Circle)
- [math]\displaystyle{ \mathbf{F_\perp} = \frac{d\mathbf{p}}{dt}_\perp = \frac{mv^2}{R} \mathbf{\hat n} }[/math], where
- [math]\displaystyle{ m = 85 \ \text{kg} }[/math] (Mass of Tarzan)
- [math]\displaystyle{ v = 13.4 \ \frac{m}{s} }[/math] (Speed at this point in time)
- [math]\displaystyle{ R = 8 \ \text{meters} }[/math] (Length of the vine)
- Taking the magnitude of each side we see that:
- [math]\displaystyle{ |\mathbf{F_\perp}| = \frac{mv^2}{R} }[/math]
- The forces acting on Tarzan along the perpendicular axis are the perpendicular component of gravity ([math]\displaystyle{ |\mathbf{F_g}| \text{sin}(\phi) }[/math]) and the force of tension ([math]\displaystyle{ |\mathbf{F_T}| }[/math]). Using this fact we can set up these equations:
- [math]\displaystyle{ |\mathbf{F_\perp}| = \frac{mv^2}{R} = |\mathbf{F_T}| - |\mathbf{F_g}| \text{sin}(\theta) }[/math]
- Therefore:
- [math]\displaystyle{ |\mathbf{F_T}| = \frac{mv^2}{R} + |\mathbf{F_g}| \text{sin}(\theta) }[/math]
- By using some right triangle trigonometry, we find [math]\displaystyle{ \phi }[/math] to be [math]\displaystyle{ 50^\text{o} }[/math]. We also note that the magnitude of the gravitational force is [math]\displaystyle{ mg }[/math], where [math]\displaystyle{ g \ \text{is} \ 9.81 \frac{m}{s^2} }[/math].
- Plugging in values gives:
- [math]\displaystyle{ |\mathbf{F_T}| = \frac{85 \times (13.4)^2}{8} + 85 \times 9.81 \times \text{sin}(50^\text{o}) }[/math]
- Which gives:
- [math]\displaystyle{ |\mathbf{F_T}| = 2546.6 \ \text{Newtons} }[/math]
Difficult
It can be fairly difficult to understand when there are other factors that influence the perpendicular component of the change of momentum, or when an individual needs to identify another influential force in that axis. For instance, in the Ferris Wheel example, when asked about having to find the necessary velocity for the rider to feel weightless, the individual needs to understand that there is a surface contact force that is also in play and in this case needs to be 0, in which case gravitational force is equal to [math]\displaystyle{ {\frac{m v^{2}}{R}} }[/math].
If a person on the Ferris Wheel is not positioned on the x- or y-axes, we cannot assume that the gravitational and contact forces are acting the same way as when the person is sitting on the Cartesian coordinate system. The reason we chose this coordinate system is because it coincides with the directions of the parallel and perpendicular forces. An oriented coordinate system must be created to accommodate for this change. It will be aligned with [math]\displaystyle{ \hat n }[/math] and [math]\displaystyle{ \hat p }[/math] (perpendicular and parallel directions, respectively).
Example:
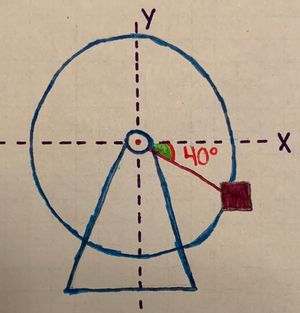
A Ferris Wheel has a radius [math]\displaystyle{ R }[/math] and rotates counter-clockwise with a constant angular rate [math]\displaystyle{ \omega }[/math]. A person with a mass [math]\displaystyle{ m }[/math] is riding in the gondola at an angle of [math]\displaystyle{ \theta = 40^\text{o} }[/math] below the x-axis as shown in the sketch.
- a) What are the magnitudes of the parallel and perpendicular components of the contact forces ([math]\displaystyle{ \mathbf{F_{c_\parallel}} \ \text{and} \ \mathbf{F_{c_\perp}} }[/math])?
- First we will draw a free body diagram for a person in a gondola:
- Notice the four different axes drawn. The x and y axes are drawn in their traditional positions, but we have also added two axes to represent the parallel and perpendicular directions for the rider's momentum.
- We will first look for an expression of the magnitude of the parallel contact force
- To do this, we want to sum the components of the forces working along the parallel axis. Once we sum them, we can set them equal to [math]\displaystyle{ 0 }[/math] because the rider moves with a constant angular velocity with a constant radius. (Remember [math]\displaystyle{ v = R\omega }[/math] for rotations, so the speed of the ride is constant, and thus the parallel component of the rate of change in momentum is [math]\displaystyle{ 0 }[/math]):
- [math]\displaystyle{ |\mathbf{F_\parallel}| = |\mathbf{F_{c_\parallel}}| - |\mathbf{F_{g_\parallel}}| = 0 }[/math]
- Since we know what the parallel component of gravity is equal to, we can simplify this expression for the parallel component of the contact force:
- [math]\displaystyle{ |\mathbf{F_{c_\parallel}}| = |\mathbf{F_{g_\parallel}}| = mg \ \text{sin}(90^\text{o} - \theta) = mg \ \text{sin}(50^\text{o}) }[/math]
- Now we will look for the contact force in the perpendicular direction, in a fashion similar to above:
- [math]\displaystyle{ |\mathbf{F_\perp}| = |\mathbf{F_{c_\perp}}| - |\mathbf{F_{g_\perp}}| = \frac{mv^2}{R} }[/math]
- We can set the net perpendicular force equal to [math]\displaystyle{ \frac{mv^2}{R} }[/math] based on our discussion in Perpendicular Component and The Kissing Circle.
- Now, we substitute [math]\displaystyle{ R\omega }[/math] for [math]\displaystyle{ v }[/math] to get:
- [math]\displaystyle{ |\mathbf{F_{c_\perp}}| - |\mathbf{F_{g_\perp}}| = \frac{m(R\omega)^2}{R} = mR\omega^2 }[/math]
- Using some right triangle trigonometry, we can create an expression for [math]\displaystyle{ |\mathbf{F_{g_\perp}}| }[/math]:
- [math]\displaystyle{ |\mathbf{F_{g_\perp}}| = mg \ \text{cos}(90^\text{o} - \theta) = mg \ \text{cos}(50^\text{o}) }[/math]
- Therefore:
- [math]\displaystyle{ |\mathbf{F_{c_\perp}}| = mR\omega^2 + mg \ \text{cos}(50^\text{o}) }[/math]
The problem is also worked out in the video below:
Connectedness
- How is this topic connected to something that you are interested in?
Curving motion is heavily employed when observing planetary orbits, something I find highly fascinating. Although in reality these orbits aren't perfectly circular as we often make them out to be, they still heavily demonstrate the ideas of curving motion and especially [math]\displaystyle{ {\frac{m v^{2}}{R}} }[/math]!
- How is it connected to your major?
As of now I am a CS major, and using vPython to model curving motion animations among many things helps apply programming ideas such as iteration and variable update.
Specifically within learning the DEvices and Intelligence Threads, basically introduction to robotics, curving (circular) motion presents itself as opportunity to learn how to attribute such to robotics so that they may be better able to be applied to complex tasks or complete tasks in general with increased range and efficiency.
- Is there an interesting industrial application?
Centripetal and Centrifugal forces can be found in many industrial applications, as curved motion is a very frequent occurrence when observing interactions between various objects. For instance, a centrifuge using these mechanics helps astronauts train for higher effective gravity.
Specifically in areas of applying robotics to search and rescue operations, curving (circular) motion allows such small bodies the flexibility to enter crevices inaccessible from the outside to the human body, especially with rescue gear, to try and locate people or objects.
What's more is that more softer and miniscule robot bodies, curving (circular) motion allows for ease of traverse through sensitive and delicate areas, like organs and veins/arteries.
History
The study of curving motion is a direct digression of the studies in classical mechanics brought about by Newton's Laws of the 1600's. The laws of curving motion are a direct result of Newton's Second Law.
Having been able to condense even the most complex of physics concepts into easy-to-understand, foundational laws, he is the first referenced when exploring curving motion and applying it to problems.
As with most science, curving motion is built upon existing ideas, observations, data, etc. One could argue that what got the ball rolling that would inevitably lead to curving motion as it is known in the modern day began with the, then controversial, ideas of Copernicus, mid-15th century. He proposed the heliocentric theory, where the Sun is the fixed point around which the planets orbit. Additionally, the Earth is instead one of these planets which, besides orbiting the Sun annually, also completely turns on its axis daily. This slow but extended axis rotation accounts for the same motion of the equinoxes. The complete theory and works wouldn’t be published until the year of his death in 1543, in “Six Books Concerning the Revolutions of the Heavenly Orbs.” It was revolutionary, but built upon existing ideas of thinking, and other observations. Copernicus simply offered new perspective. For instance, Plato and Eudoxus noted the movement of certain planets seemed to suggest they never strayed to far from the sun, though they still thought Earth was at the center. Aristarchus of Samos and the Pythagoreans had similarly proposed a heliocentric system, or rather a “central fire” as well.
At the same time as Copernicus, however, was a famous astronomer know as Tycho Brahe, well regarded for his distinctly unprecedented data from his different approach to observing “the heavens”. In 1563 he would observe Jupiter overtaking the Sun as the planets moved. From even observations as simple as this, he realized existing tables and Copernicus’ model (influenced by existed observations) were off by a month. Brahe’s revolutionary contributions to astronomy included that he demonstrated better data could help construct more robust models, of which he went forward in creating his own. With increased observations inconsistent with the longstanding belief that the celestial realm was a place of perfect and unchanging fixed stars, and the appearance of a comet in 1577, he had additional evidence that things did change and did move in the celestial sphere. Using careful measurements, Brahe discerned that the comet was outside the moon’s sphere, and later suggested it was moving through the spheres of different planets. So, Brahe put forward a new model for the cosmos, where the planets orbited the sun, and the sun and the moon orbited the Earth. Keeping with his observations of the new star and the comet, his model allowed the path of the planet Mars to cross through the path of the sun. While seen as a loss of progress from Copernicus’ heliocentric model, there was important value to be found in the detail of Brahe’s model, if not the “star focus.” This system had the advantage of resolving the problem of stellar parallax. A stubborn critique of Copernicus's model (and even of Aristarchus model in ancient Greece) was that with a moving Earth one should expect to see parallax movement of the stars. Copernicus' argued the stars were too far to detect parallax. Still, the distance required to make this work was so massive as to be a problem for the system, and was more so based on observation than calculation.
Brahe's system allowed for the circles in the heavens to intersect. Brahe's model was revolutionary in the detail and data it presented in a competitive way to make sense of the data/observations the heavens provided.
Following Brahe, there is Kepler, born in 1571, who, using Brahe’s observational data and models, was determined to explore how the different shapes of Platonic solids could be combined to explain a superstructure for the heavens, and how the movements and patterns of the heavens could be mapped on to scales. He continuously proposed the deep intertwining of geometry and physics, which led to a new shape of the planetary orbits. In Astronomie Nova (1609), Kepler presented extensive research on the orbit of Mars. Utilizing Tycho Brahe's observational data, Kepler would fine tune the movements of the planets and demonstrate Mars’ movement could be described as an ellipse. He demonstrates in Astronomia Nova the difference between a perfect circle and the more pinched/squished inner ellipse. The general belief was that the heavens’ motions were only in perfect circles. However, Kepler was able to mathematically describe ellipses that closely fit the paths the planets moved through in the heavens. The ellipse enabled the removal of the epicycles and could account for the path of the planets in a single shape. His commitment to order and structure pushed him to recalculate and rework until he figured out how to represent the orbits of the planets. Alongside describing the elliptical nature of orbits, Astronomie Nova offered initial arguments for a force of attraction that could organize and hold this kind of system together. Kepler's work foreshadowed the discovery of one of the fundamental forces of physics, the law of gravity, by Newton.
If Kepler's laws define the motion of the planets, Newton's laws define motion. Thinking on Kepler's laws, Newton realized that all motion followed the same basic principles. His laws of motion and gravity explained Earth’s annual journey around the Sun. Sun exerts a constant pull on Earth as it move straight forward in the universe. This force bends Earth’s path toward the Sun, pulling the planet into an elliptical (almost circular) orbit. In unifying all motion, Newton shifted the scientific perspective to look for large, unifying patterns in nature. Newton’s second law is most recognizable in its mathematical form, the iconic equation: F=ma. The strength of the force (F) is defined by how much it changes the motion (acceleration, a) of an object with some mass (m). Newton 's laws were first published in his work Philosophiae Naturalis Principia Mathematica (1687).
Therefore, an object moving in uniform (constant speed) circular (constant radius) motion is still accelerating because it is constantly changing direction. Using Newton's 2nd law, F = ma, we can determine the mass of the object in uniform circular motion if we measure the acceleration and the force responsible.
See also
Further Reading
- Linear Momentum
- Newton's Second Law: the Momentum Principle
- Net Force
- Gravitational Force Near Earth
- Free Body Diagram
- Tension
External Links
References
2) https://www.britannica.com/biography/Nicolaus-Copernicus