Net Force
This page defines the net force acting on a system.
Main Idea
The net force acting on a system (such as a particle, collection of particles, or rigid body) is defined as the vector sum of all of the forces acting on the system. People are interested in net force because a net force acting on a system affects its motion. More specifically, a nonzero net force causes the system's Linear Momentum to change over time in the direction of the net force, as described by Newton's Second Law: the Momentum Principle. For a system of constant mass, this change in momentum takes the form of Acceleration in the direction of the net force. Conversely, a net force of 0 acting on a system means that, according to Newton's Second Law, the system is travelling with a constant momentum. For a system of constant mass, this means that the system is travelling at constant speed, which may be zero or nonzero. The fact that motion is possible with a net force of 0 may be be counter-intuitive, but recall that Newton's First Law states that objects in motion stay in motion unless a (nonzero net) force acts on it. For example, consider a rock thrown in empty space. It will travel at a constant speed in a straight line forever unless it encounters something that can exert a force on it.
The effects of a net force do not depend on the forces comprising it. For example, if the forces [math]\displaystyle{ f_1 = \lt 1, 1, 0 \gt }[/math] N and [math]\displaystyle{ f_1 = \lt 1, -1, 0 \gt }[/math] N act on a system, the net force would be [math]\displaystyle{ F_{net} = \lt 1, 0, 0 \gt }[/math] N. Similarly, if the forces [math]\displaystyle{ f_1 = \lt 2, 0, 0 \gt }[/math] N and [math]\displaystyle{ f_1 = \lt -1, 0, 0 \gt }[/math] N act on a system, the net force would also be [math]\displaystyle{ F_{net} = \lt 1, 0, 0 \gt }[/math] N. In both cases, the net force is the same, so momentum of the system will be affected in the same way for both net forces.
A Mathematical Model
By definition,
[math]\displaystyle{ \vec{F}_{net} = \sum_i \vec{f}_i }[/math]
Sometimes the individual force vectors are simply given in component form. In this case, recall that to add the force vectors, their corresponding components of the vectors should be added to yield the components of the resultant vector.
At least as often, the individual force vectors are not given in component form but have known magnitudes and directions. In this case, coordinate axes should be chosen and the forces should be decomposed into components along those axes. If it is possible to predict the direction of the net force using physical intuition, the axes should be chosen so that one of them is parallel to this net force. Otherwise, The axes should be chosen so that as many forces as possible are parallel to them an axis, reducing the need to decompose them.
Recall that some forces, such as tension and the normal force, do not have readily available magnitudes; their magnitudes must be found based on the magnitudes of other forces.
A Computational Model
Fortunately, vector addition is very easy in computer programming languages such as vPython. As long as the individual forces acting on a particle are calculated as vectors, when they are added together, vPython will add their components to find the resultant vector.
Finding the net force is an essential part of the Iterative Prediction process, which is used in most physics simulations. Below is an excerpt from a vPython program that uses iterative prediction to simulate the motion of a ball on a spring. The seven lines shown are responsible for the three steps of iterative prediction.
#1 Fspring = -k*s #2 Fgravmag = mball * g #3 Fgrav = Fgravmag * vector(0,-1,0) #4 Fnet = Fspring+Fgrav #5 pball = pball + Fnet * deltat #6 vball = pball / mball #7 ball.pos=ball.pos+vball*deltat
Here, the spring force and the gravitational force are found using formulas (lines 1-3). Then, they are added together to get the net force on the ball (line 4). The net force is then used to update the momentum of the ball (line 5). In line 6 the velocity is updated based on the new momentum, and line 7 the position is updated based on the new velocity. Without net force calculations, tracing an object's path would be impossible.
Examples
1. (Simple)
When calculating net force, it is useful to construct a free body diagram. A free body diagram is a physical representation of the external forces applied to a system. Often, arrows are used to represent forces. In this example, forces are displayed acting on a box.
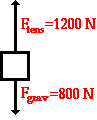
The first box is being suspended by a rope (but it is not quite at equilibrium), so its free body diagram looks like this:
What is the net force acting on this box?
Solution:
Assume that down is the negative y direction, and you can easily write vector representations of the forces and add them up to find the sum, which is the net force:
[math]\displaystyle{ Fnet = (0, 1200, 0) }[/math]N[math]\displaystyle{ + (0, -800, 0) }[/math]N
[math]\displaystyle{ Fnet = (0, 400, 0) }[/math]N
The second box is falling, but it has significant air resistance:
What is the net force acting on this box?
Solution:
[math]\displaystyle{ Fnet = (0, 600, 0) }[/math]N[math]\displaystyle{ + (0, -800, 0) }[/math]N
[math]\displaystyle{ Fnet = (0, -200, 0) }[/math]N
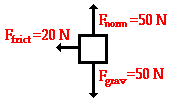
The third box is on the ground and is sliding to the right, but slowing down because of friction. It has both x-component forces and y-component forces. It is important to put these in the right place in the vector coordinates.
What is the net force acting on this box?
Solution:
[math]\displaystyle{ Fnet = (0, 50, 0) }[/math]N[math]\displaystyle{ + (0, -50, 0) }[/math]N[math]\displaystyle{ + (-20, 0, 0) }[/math]N
[math]\displaystyle{ Fnet = (-20, 0, 0) }[/math]N
2. (Simple)
Two external forces <60,-70,0>N and <20,10,0>N, act on a system. What is the net force acting on the system?
Answer: <80,-60,0>N
Explanation:
The net force is the vector sum of its constituent forces.
[math]\displaystyle{ \vec{F}_{net} = \vec{F}_{1} + \vec{F}_{2} }[/math]
[math]\displaystyle{ \vec{F}_{net} }[/math] = <60,-70,0)N + <20,10,0>N = <80,-60,0>N
3. (Middling)
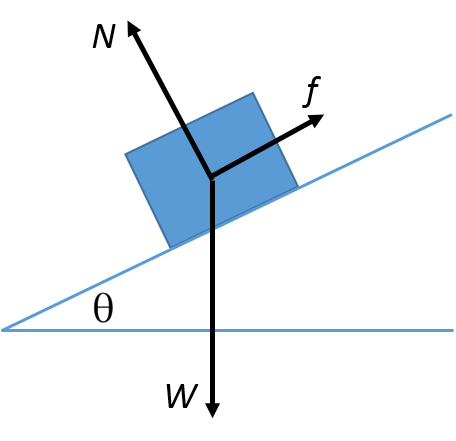
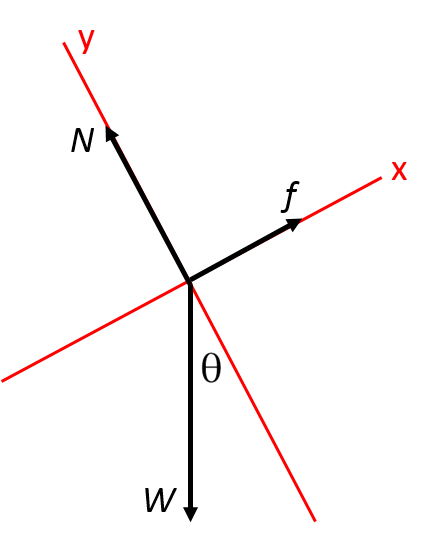
There is a box, small enough to represented as a point, sitting on a slope inclined twenty degrees with respect to the horizontal. If its mass is 10 kg, what does the magnitude of the force of static friction (pointing up the hill) have to be for net force to be zero? In that case, what is the magnitude of the normal force? (All forces are measured in newtons, and the acceleration due to gravity [math]\displaystyle{ = g = 9.8 }[/math] [math]\displaystyle{ m/(s^2) }[/math]).
Solution:
Let [math]\displaystyle{ f }[/math] = force of friction, [math]\displaystyle{ W }[/math] = weight of the object, and [math]\displaystyle{ N = }[/math] normal force. (The pictures are not to scale.)
First, we have to identify our coordinate axes. We could have the typical horizontal x-axis and vertical y-axis (and we know where to put [math]\displaystyle{ θ }[/math] using similar triangles):
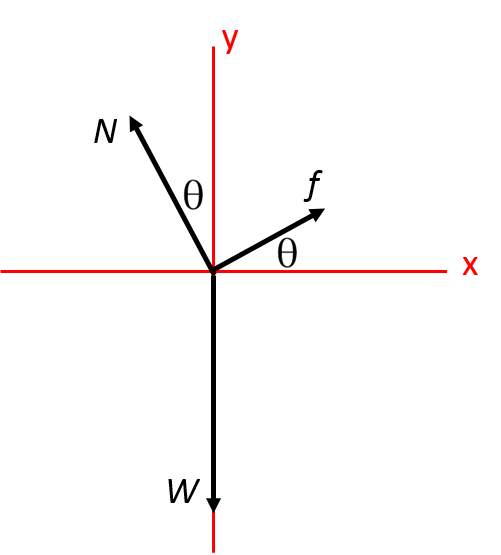
But, that leaves us with two forces that have to be decomposed into x- and y- components. It makes more sense to draw the axes rotated twenty degrees counterclockwise, like this:
[math]\displaystyle{ W }[/math] is easy to find, since it's just mass times acceleration due to gravity, both of which are known quantities.
[math]\displaystyle{ W = mg = (10 }[/math] [math]\displaystyle{ kg)*(9.8 }[/math] [math]\displaystyle{ m/(s^2)) = 98 }[/math] [math]\displaystyle{ newtons }[/math]
Now we are ready to solve for the frictional force. It acts in the positive x direction, and we know that the net force in the x direction has to be zero, so we have to identify the other forces that act in the positive or negative x direction. In this case, it's only a component of the weight, which points in the negative x direction. Using simple trigonometry, we find that that is
[math]\displaystyle{ -W*sin(θ) }[/math]
So we can write our equilibrium equation like this:
[math]\displaystyle{ Fnetx = f - W*sin(θ) = 0 }[/math]
Then, all we have to do is solve for the friction force [math]\displaystyle{ f }[/math], since [math]\displaystyle{ W }[/math] and [math]\displaystyle{ θ }[/math] are known quantities.
[math]\displaystyle{ f = W*sin(θ) = (98 }[/math] N[math]\displaystyle{ )*sin(20°) = 33.51797405 }[/math] N, which is about equal to [math]\displaystyle{ 33.5 }[/math] N.
Now we have to solve for the normal force. It acts in the positive y direction, and we know that the net force in the y direction has to be zero, so we have to identify the other forces that act in the positive or negative y direction. In this case, the only one is the other component of the weight, which points in the negative y direction. Using simple trigonometry, we find that that is
[math]\displaystyle{ -W*cos(θ) }[/math]
So we can write our equilibrium equation like this:
[math]\displaystyle{ Fnety = N - W*cos(θ) = 0 }[/math]
Then, all we have to do is solve for [math]\displaystyle{ N }[/math], since [math]\displaystyle{ W }[/math] and [math]\displaystyle{ θ }[/math] are known quantities.
[math]\displaystyle{ N = W*cos(θ) = (98 }[/math] N[math]\displaystyle{ )*cos(20°) = 92.08987684 }[/math] N, which is about equal to [math]\displaystyle{ 92.1 }[/math] N.
Connectedness
Force and net force have applications in all parts of the physical universe. If an object accelerates, this acceleration can be attributed to a nonzero net force. If an object travels at a constant speed, that can be attributed to a net force of zero. Even objects at rest remain that way because of a careful balancing of forces whose vector sum is 0.
History
Some of the earliest records of humans' musings about force come from Aristotle. Aristotle observed the natural world and made assumptions and equations based on what he saw. He described all motion as being either "natural"--circular and infinite OR finite, up and down, in a straight line--or "violent." Aristotle had issues with projectile motion as he could not reconcile the continuing movement of the object with the lack of force being applied. He ended up concluding that the air provides a simultaneous resistant and accelerating force to the object.
These ideas were challenged by Renaissance men such as John Philoponus, John Buridan, and Oresme, with a clear understanding of the conservation of linear momentum not arriving to the world until Descartes. The most famous face we associate with forces in Physics is Sir Isaac Newton, who defined force as it is still used today. Newton initially believed in the idea of impetus, the belief that a projectile has an internal force that keeps it moving, and in the idea of transfer, that objects give up parts of their force during a collision. These notions were incorrect, but he was later able to correctly separate the ideas of force and momentum. Thus, the second law of motion was established and with it the relationship between force and motion.
See also
External links
Physics Classroom: Net Force Physics Classroom: Drawing Free Body Diagrams
References
Cardenas, Richard. "What is Net Force? - Definition, Magnitude & Equations." Web. 30 Nov 2015. http://study.com/academy/lesson/what-is-net-force-definition-magnitude-equations.html
"Net Force." Wikipedia: The Free Encyclopedia. Wikimedia Foundation, Inc. Web. 30 Nov 2015. https://en.wikipedia.org/wiki/Net_force
The Physics Classroom. "Determining the Net Force." Web. 30 Nov 2015. http://www.physicsclassroom.com/class/newtlaws/Lesson-2/Determining-the-Net-Force
Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Modern Mechanics. Hoboken, NJ: Wiley, 2011. Print.
Stinner, Arthur. "The story of force: from Aristotle to Einstein." Physics Education. 1994. Web. 30 Nov 2015. http://www.arthurstinner.com/stinner/pdfs/1994-storyofforce.pdf