Parallel Circuits

Claimed by Alex Oshin (Fall 2017)

The Main Idea

A simple parallel circuit. R1 and R2 are in parallel because they lie on different branches of the circuit.

Components of a circuit can be connected in two main ways, in series or in parallel. This page focuses on components connected in parallel, which means that the components are connected such that the same voltage is applied to each component. A parallel circuit is a circuit that is connected entirely in parallel. Each component in a parallel circuit occupies its own branch, or path in the circuit, and these branches are connected at locations called nodes. Thus a charge passing through the circuit has multiple possible paths that it can take when it reaches a node. This property is the reason why adding an additional resistor in a parallel circuit results in a decreased total resistance of the circuit (since there is an additional path that the charges can follow). Likewise, if a path is removed, or if the circuit is broken in a single path, more charge is forced to flow through the remaining paths, and the total resistance increases.

A Mathematical Model

Ohm's Law is essential for understanding circuits, and in particular, the relationship between current, voltage, and resistance.

[math]\displaystyle{ I=\frac{V}{R} }[/math]

The voltage is the same for all elements of a parallel circuit.

[math]\displaystyle{ V_{total}=V_1=V_2=...=V_n }[/math]

The total resistance of a parallel circuit is the reciprocal of the sum of the reciprocals of the individual resistances.

[math]\displaystyle{ \frac{1}{R_{total}}=\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_n} }[/math]

Applying Ohm's Law to these two equations, we can find an equation for the total current of a parallel circuit.

[math]\displaystyle{ I_{total}=V(\frac{1}{R_{1}}+\frac{1}{R_{2}}+...+\frac{1}{R_{n}}) }[/math]

And the current flowing through a component with resistance [math]\displaystyle{ R_{i} }[/math] will be:

[math]\displaystyle{ I_{i}=\frac{V}{R_{i}} }[/math]

These results are consistent with Kirchhoff's circuit laws, and can be similarly derived.

A Computational Model

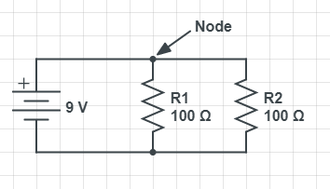
A schematic is the easiest way to visualize a parallel circuit, and circuits in general.

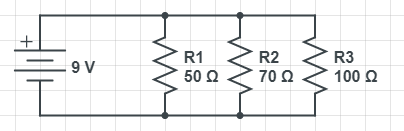
The circuit above contains a battery and three resistors. Notice R1, R2, and R3 occupy different branches of the circuit. They are connected by only two nodes, one at the top of the circuit and one at the bottom, even though it may seem like there are four nodes in the schematic.

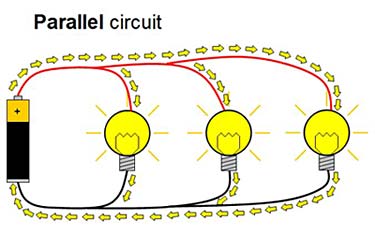
The following image shows a real-world example.

Each lightbulb acts like a resistor in the previous circuit schematic.

This website is a simple circuit builder that can be used to simulate circuits in parallel(or in series).

This website is a more complicated circuit builder that can also be used to model parallel or series circuits and test the differences in current, voltage, and resistance with with various setups.

Examples

Simple

Question

Calculate the total resistance of this parallel circuit.

Solution

Start by applying the formula for the resistance of a parallel circuit.

[math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} }[/math]

In this case, we simply need to substitute the values of [math]\displaystyle{ R_1 }[/math], [math]\displaystyle{ R_2 }[/math], and [math]\displaystyle{ R_3 }[/math] into the formula, and solve for [math]\displaystyle{ R_{total} }[/math].

[math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{50Ω}+\frac{1}{70Ω}+\frac{1}{100Ω} }[/math]

[math]\displaystyle{ {R}_{total}=22.581Ω }[/math]

Middling

Question

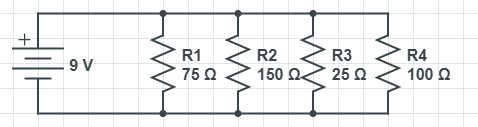
Calculate the total current of the following circuit.

Solution

Start by finding the total resistance of the circuit.

[math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4} }[/math]

[math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{75Ω}+\frac{1}{150Ω}+\frac{1}{25Ω}+\frac{1}{100Ω} }[/math]

[math]\displaystyle{ {R}_{total}=14.286Ω }[/math]

From here, we can use Ohm's Law to find the total current [math]\displaystyle{ I_{total} }[/math]

[math]\displaystyle{ I=\frac{V}{R} }[/math]

[math]\displaystyle{ I_{total}=\frac{V}{R_{total}} }[/math]

[math]\displaystyle{ I_{total}=\frac{9V}{14.286Ω} }[/math]

[math]\displaystyle{ I_{total}=0.63A }[/math]

This problem can be solved in one step by combining Ohm's Law with what we know about the resistance of a parallel circuit (see A Mathematical Model above)

[math]\displaystyle{ I_{total}=V(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}) }[/math]

[math]\displaystyle{ I_{total}=(9V)(\frac{1}{75Ω}+\frac{1}{150Ω}+\frac{1}{25Ω}+\frac{1}{100Ω}) }[/math]

[math]\displaystyle{ I_{total}=0.63A }[/math]

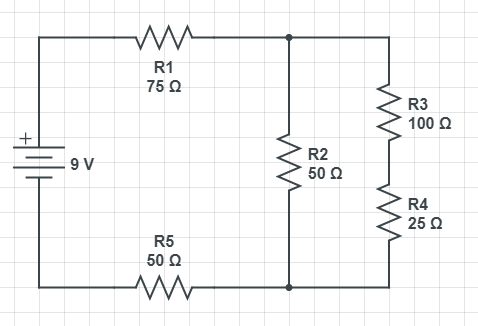
Difficult

Question

Calculate the total current of the following circuit.

Solution

This problem relies on understanding both series and parallel circuits. See Series Circuits if any of the following assumptions are unclear.

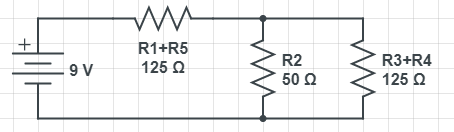
This easiest way to solve this problem is to calculate the total resistance of the circuit, and then use Ohm's Law to calculate the total current. Since resistors in series can be simplified into a single resistor with resistance equal to the sum of all the resistors in series, we can simplify the circuit by combining R1 and R5, as well as R3 and R4.

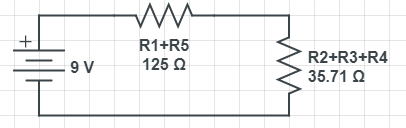
Since R2 and R3+R4 are connected in parallel, we can use what we know about parallel circuits to further simplify the circuit.

[math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{R2}+\frac{1}{R3+R4} }[/math]

[math]\displaystyle{ R_{total}=35.714Ω }[/math]

Finally, these two simplified resistors are connected in series, so we can find the total resistance.

[math]\displaystyle{ R_{total}=(R1+R5)+(R2+R3+R4) }[/math]

[math]\displaystyle{ R_{total}=160.714Ω }[/math]

Now we can use Ohm's Law to calculate the total current.

[math]\displaystyle{ I=\frac{V}{R} }[/math]

[math]\displaystyle{ I_{total}=\frac{V}{R_{total}} }[/math]

[math]\displaystyle{ I_{total}=\frac{9V}{160.714Ω} }[/math]

[math]\displaystyle{ I_{total}=0.056A }[/math]

Connectedness

Circuits can be applied to many areas. However, it is rare that we can find a true parallel circuit in the real world. Many times, real world examples combine both series and parallel circuits. But with some generalizations, we can find examples of parallel circuits in our everyday lives. For example, your phone's battery supplies voltage to the various components and devices within your phone, such as the processor, memory, display, etc., and these are all connected in parallel. Electricity to houses is typically set up in parallel so that one appliance or light can be used without having to use all of them(which would be necessary in series to complete the circuit). On a larger scale, electric or power grids distribute electricity in parallel to the consumers that need it.

History

Electric circuits would not be possible without a constant source of current. Therefore, the battery was a necessary invention for the circuit to be developed. The invention of the battery is generally attributed to Alessandro Volta, who stacked pairs of zinc and copper soaked in brine, and realized that it produced current. The SI unit for electric potential, the volt, is named after him in his honor.

These, and all later batteries, produce direct current, or DC for short, which supplies a constant current in one direction. Circuits created using these batteries are very similar to the circuits discussed on this page. In fact, these circuits formed the basis for Thomas Edison's invention of the incandescent light bulb, and later his attempt at distributing electricity across a power grid.

However, DC has an inherent disadvantage in that there is a large power loss over long distances due the resistance of the wires used to transport the electricity. As such, Edison's rival and contemporary Nikola Tesla used alternating current, or AC, to efficiently distribute electricity over long distances. AC periodically changes direction, and this property allows it to travel long distances with little power loss, and it also generates relatively little heat during the process (another problem of DC). Using electric devices known as transformers, it is possible to change voltage levels in an AC circuit, and this forms the foundation for the electricity that is sent to your home. You will learn later about how a transformer works when you study magnetic induction.

After the invention of lighting, and power grids that could effectively distribute electricity, the further development of home appliances and other electric devices meant that the influence of electric circuits would continue to spread. Nowadays, it is hard to imagine how different our lives would be if we did not have electricity.

Parallel Circuits

Contents

The Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu