Loop Rule

From Physics Book
Jump to navigation Jump to search

Claimed by Sahil Arora (Fall 2016)

The Loop Rule, also known as Kirchhoff's Second Law, is a fundamental principle of electric circuits which states that the sum of potential differences around a closed circuit is equal to zero. More simply, when you travel around an entire circuit loop, you will return to the starting voltage. Note that is only true when the magnetic field is neither fluctuating nor time varying. If a changing magnetic field links the closed loop, then the principle of energy conservation does not apply to the electric field, causing the Loop Rule to be inaccurate in this scenario.

The Main Idea

(The Energy Principle and the Loop Rule)

The loop rule simply states that in any round trip path in a circuit, Electric Potential equals zero. Keep in mind that this applies through ANY round trip path; there can be multiple round trip paths through more complex circuits. This principle deals with the conservation of energy within a circuit. Loop Rule and Node Rule are the two fundamental principles of electric circuits and are used to determine the behaviors of electric circuits. This principle is often used to solve for resistance or current passing through of light bulbs and other resistors, as well as the capacitance or charge of capacitors in a circuit.

A Visual Model

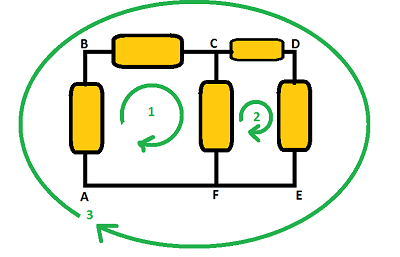
LOOP 1: [math]\displaystyle{ \Delta {V}_{AB} + \Delta {V}_{BC} + \Delta {V}_{CF} + \Delta {V}_{FA} = 0 }[/math]

LOOP 2: [math]\displaystyle{ \Delta {V}_{FC} + \Delta {V}_{CD} + \Delta {V}_{DE} + \Delta {V}_{EF} = 0 }[/math]

LOOP 3: [math]\displaystyle{ \Delta {V}_{AB} + \Delta {V}_{BC} + \Delta {V}_{CD} + \Delta {V}_{DE} + \Delta {V}_{EF} + \Delta {V}_{FA} = 0 }[/math]


To figure out the sign of the voltages, act as an observer walking along the path. Start at the negative end of the emf and continue walking along the path. The emf will be positive in the loop rule because you are moving from low to high voltage. Once you reach a resistor or capacitor, this will be negative in the loop rule equation because it is high to low voltage. Continue along the path until you return to the starting position.


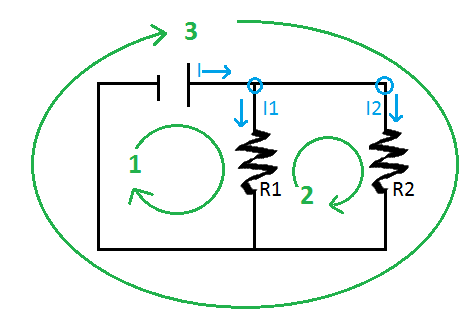
LOOP 1: [math]\displaystyle{ emf - I_1R_1 = 0 }[/math]

LOOP 2: [math]\displaystyle{ -I_1R_1 + I_2R_2 = 0 }[/math]

LOOP 3: [math]\displaystyle{ emf - I_2R_2 = 0 }[/math]


A Mathematical Model

A mathematical representation is:

[math]\displaystyle{ \sum_{i=1}^n {V}_{i} = 0 }[/math]

where n is the number of voltages being measured in the loop, as well as

[math]\displaystyle{ \Delta {V}_{1} + \Delta {V}_{2} + \space.... = 0 }[/math]

along any closed path in a circuit.

A Computational Model

This is a pretty cool model of how the Loop Rule is applied and calculated. You can change the direction of the current as well as the voltage of the batteries. To turn off the voice, press the Audio Tutorial button. To test your knowledge, click on the Concept Questions and Notes buttons, they have some questions and useful information in them.

This is an online circuit simulator. It opens up with an LRC circuit that has current running through it. The graphs on the bottom show the voltage as the current runs through the circuit. You can see that after a full loop the voltage is 0, verifying the loop rule. You can make all sorts of different circuits and loops and see for yourself.

Examples

Simple

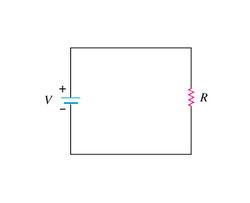
The circuit shown above consists of a single battery and a single resistor. The resistance of the wires is negligible for this problem.

Question

If the [math]\displaystyle{ emf }[/math] is 5 V and the resistance of the resistor is 10 ohms, what is the current passing through the resistor?

Solution

Although we can solve this using the [math]\displaystyle{ V = IR }[/math] equation for the whole loop, let's examine this problem using the loop rule equation.

The loop rule equation would be [math]\displaystyle{ {V}_{battery} - {V}_{resistor} = 0 }[/math]


Since we know the [math]\displaystyle{ emf }[/math] of the battery we just need to find the potential difference through the resistor. For this we can use the equation of [math]\displaystyle{ V = IR }[/math].

Thus we now have an loop rule equation of [math]\displaystyle{ emf - IR = 0 }[/math] From here it is a relatively simple process to find the current. We can rewrite the loop rule equation as [math]\displaystyle{ emf = IR }[/math] and then plug in 5 for the emf and 10 for the resistance, leaving us with I = .5 amperes.

Middling

Question

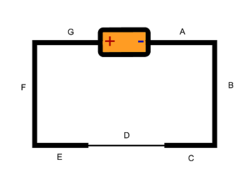
The circuit shown above consists of a single battery, whose [math]\displaystyle{ emf }[/math] is 1.3 V, and three wires made of the same material, but having different cross-sectional areas. Let the length of the thin wires be [math]\displaystyle{ {L}_{thick} }[/math] and the length of the thin wire be [math]\displaystyle{ {L}_{thin} }[/math] Find a loop rule equation that starts at the negative end of the battery and goes counterclockwise through the circuit.

Solution

When beginning this problem, you must notice that the difference in cross-sectional areas affects the electric field in each wire. Because of this we will denote the electric field at D. as [math]\displaystyle{ {E}_{D} }[/math] and the electric field everywhere else as [math]\displaystyle{ {E}_{A} }[/math]. To begin we will go around the circuit clockwise and add up each component. First, we know that the [math]\displaystyle{ emf }[/math] of the battery is 1.3 V. Then, we will add up the potential voltage of each of the wires.

Remember that the electric potential of a wire is equal to the product of the electric field and the length of the wire. From this we can now find the potential difference of each section of the wires. The electric potential of location A - C is [math]\displaystyle{ {E}_{A} * {L}_{thick} }[/math]. This is the same for the electric potential of locations E - G of the wire. For the thin section of the wire, the electric potential is [math]\displaystyle{ {E}_{D} * {L}_{thin} }[/math]. From here we just go around the circuit counterclockwise and add each potential difference to the loop rule equation.

Thus we can find that a loop rule equation is: [math]\displaystyle{ emf - 2 ({E}_{A} * {L}_{thick}) - {E}_{D} * {L}_{thin} = 0 }[/math]

This can also be rewritten as: [math]\displaystyle{ emf = 2 ({E}_{A} * {L}_{thick}) + {E}_{D} * {L}_{thin} = 0 }[/math]

Difficult

Question

For the circuit above, imagine a situation where the switch has been closed for a long time. Calculate the current at a,b,c,d,e and charge Q of the capacitor. Answer these using [math]\displaystyle{ emf, {R}_{1}, {R}_{2}, and \space C }[/math]

Solution

First, write loop rule equations for each of the possible loops in the circuit. There are 3 loop equations that are possible.

[math]\displaystyle{ emf - {I}_{1}{R}_{1} - {I}_{2}{R}_{2} = 0 }[/math]

[math]\displaystyle{ emf - {I}_{1}{R}_{1} - Q/C = 0 }[/math]

[math]\displaystyle{ {I}_{2}{R}_{2} - Q/C = 0 }[/math]

From here, we can then solve for the current passing through a,b,d and e. We also know that the current passing through these points must be the same so [math]\displaystyle{ {I}_{1} = {I}_{2} }[/math]

[math]\displaystyle{ emf - {I}_{1}{R}_{1} - {I}_{1}{R}_{2} = 0 }[/math]

[math]\displaystyle{ emf = {I}_{1}({R}_{1} + {R}_{2}) = 0 }[/math]

[math]\displaystyle{ emf/({R}_{1} + {R}_{2}) = {I}_{1} }[/math]

So the current at a,b,d,e = [math]\displaystyle{ emf/({R}_{1} + {R}_{2}) }[/math]

You must also know that once a capacitor is charging for a long time, current no longer flows through the capacitor. We can then easily solve for c because since current is no longer flowing through the capacitor, the current at c = 0.

Lastly, we will use the loop rule equation of [math]\displaystyle{ {I}_{2}{R}_{2} - Q/C = 0 }[/math] to solve for Q.

[math]\displaystyle{ {I}_{2}{R}_{2} = Q/C }[/math]

[math]\displaystyle{ C*({I}_{2}{R}_{2}) = Q }[/math]

Since [math]\displaystyle{ {I}_{1} = {I}_{2} }[/math] , [math]\displaystyle{ C*({I}_{1}{R}_{2}) = Q }[/math]

We can plug in what we found [math]\displaystyle{ {I}_{1} }[/math] equals from before.

[math]\displaystyle{ C* (emf/({R}_{1} + {R}_{2})){R}_{2}) = Q }[/math]

Lastly, Q = [math]\displaystyle{ C* (emf/({R}_{1} + {R}_{2})){R}_{2} }[/math] and we have now solved the problem.

Current at a,b,d,e = [math]\displaystyle{ emf/({R}_{1} + {R}_{2}) }[/math]

Current at c = 0

Q = [math]\displaystyle{ C* (emf/({R}_{1} + {R}_{2})){R}_{2} }[/math]

Connectedness

The Loop Rule is simply an extension of the conservation of energy applied to circuits. Circuits are ubiquitous as they are featured in almost every technology today. Our understanding of these technologies is rooted in the empirical discoveries made in the mid 19th century, and further boosted by the the advancement of theoretical knowledge due to the likes of Faraday and Maxwell.

One interesting note about Loop Rule is that is does not apply universally to all circuits. In particular, AC (alternating current) circuits at high frequencies, have a fluctuating electric charge that changes direction. This causes the electric potential of a round trip path around the circuit to no longer be zero. However, DC (direct current) circuits, and low frequency circuits in general, still follow the loop rule.

History

The Loop Rule is formally known as the Kirchhoff Voltage Laws, named after Gustav Kirchhoff, the scientist who discovered and defined this fundamental concept of electric circuits. He discovered this during his time as a student at Albertus University of Königsberg in 1845. Kirchoff went on to explore the topics of spectroscopy and black body radiation after his graduation from Albertus. Nowadays, it is used very often in electrical engineering.

Gustav Kirchhoff

See also

Further Reading

Other Circuit Concepts you can check out :

Node Rule

Components

Resistors and Conductivity

Current

Kirchoff's Circuit Laws - Wikipedia

External Links

If you want to test your knowledge, Khan Academy's DC Circuit Analysis under the Electrical Engineering Topic is an excellent resource. There are questions, videos, and written explanations to help you understand not just the loop rule, but the node rule as well. Click here to access it.

Loop Rule - Boundless.com Textbook

Doc Physics Video Lecture

Doc Physics Worked Example

Bozeman Science Lecture


References

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Loop_Rule&oldid=37989"