Node Rule
Improved by Preet Kalsi Claimed by Ingrid Cai
Improved by Sehyeong An
Improved by Nija Kurien
Improved by Jasmine Passade
Claimed by Marissa Rubino (Fall 2017)
Kirchoff's node rule, also known as Kirchoff's junction rule, further exercises the law of Conservation of Charge and states that if current is constant, all the current that flows through one junction must be equal to all the current that flows out of the junction. This rule can be applied both to conventional and electron currents. This rule is not a fundamental principle, but rather a consequence of the fundamental principle of conservation of charge and the definition of steady state.
The Main Idea
The node rule, also known as Kirchhoff's junction rule, nodal rule, current law, or first law, states that at any junction in an electrical circuit, the amount of current flowing into the junction is equal to the amount of current flowing out of the junction in steady state.
In the steady state, for many electrons flowing into and out of a node,
- electron current: [math]\displaystyle{ net\ i_{in} = net\ i_{out}, }[/math] where [math]\displaystyle{ i = nA\mu }[/math][math]\displaystyle{ E }[/math]
- conventional current: [math]\displaystyle{ net\ I_{in} = net\ I_{out}, }[/math] where [math]\displaystyle{ I = |q|nA\mu }[/math][math]\displaystyle{ E }[/math]
Conservation of Charge
This rule is an application of the conservation of electric charge, basically that charge within a circuit cannot be created or lost. During the flow process around the circuit, there is no loss of any charge, thus the total current in any cross-section of the circuit is the same. If there are no nodes in the loop, the conventional current is the same throughout the loop.
Limitations
1. Time-Varying Currents
Kirchhoff's law is based off the conservation of charge along with the nature of conductors. This law assumes that current will immediately flow from one end of the conductor to the other, which may not be true for time-varying currents, especially with higher frequencies.
2. Regions vs Circuits
Throughout a region, the charge can vary and be non-uniform, unlike in a wire. According to the law of conservation of charge, the only way to have a non-uniform charge density is if there is a net flow of current in or out of the region, which clearly violates the Node Rule. Therefore the node rule cannot be applied to regions with non-uniform charge densities. When looking at a junction in an electric circuit, we are looking at a point and therefore the point (which is infinitesimally small) must have a uniform charge distribution. In general, wires should have a uniform charge distribution across their length, because they are conductors and allow for the movement of charge.
3. Non-Steady State
The node rule can only be applied to the steady state. Thus, when considering the capacitor, the node rule is applied to the capacitor as a whole not just one plate of the capacitor.
Solving Circuits
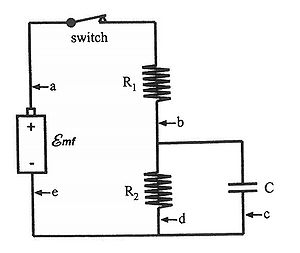
In order to solve circuits, we must first define a couple characteristics of circuits.
- The voltage of a (perfect, or non-resistive) wire is equal to its length (in meters) times its electric field.
- The voltage of an ohmic resistor (including a resistive wire) is equal to current times resistance.
- The voltage of a capacitor is equal to the charge on the capacitor divided by its capacitance.
There are other characteristics and equations that may be useful, but these three are the most important and used. If you are confused by any of the components of circuits mentioned above, visit the Components page.
To the right is a circuit. Using the node and loop rules we will find the current at points a, b, c, d, and e, and the charge on the capacitor after the switch has been closed for a very long time.
First you must realize that when the capacitor is fully charged, no current will flow through the capacitor, which is an important characteristic of a capacitor. From this we can say that the current through point c is 0.
Using the node rule, we can see that the current through resistor 1 and resistor 2 must be the same because no current flows through the wire connected the capacitor, so then all of the current must flow through one loop containing both resistors. So the current at a, b, d and e must all be the same. Due to the loop rule, the emf of the battery must be equal to I*R1 + I*R2. Therefore, I = emf/(R1 + R2); this is the current through points a, b, d and e. Using the loop rule, we can look at the loop containing the capacitor and resistor 2. We know the voltage in resistor 2 is equal to I*R2. We know the voltage of the capacitor is equal to its charge divided by C (its capacitance). Because of the loop rule, we know that these two voltages must be equal, so I*R2 = Q/C. Therefore, Q = I*R2*C. Replacing I with the current we found above, Q = (emf/(R1 + R2))*R2*C. As you can see, in order to solve this circuit, we had to use the node rule. In fact, we used the node rule at the very beginning of solving this circuit and there was no way possible we could have solved this problem without it.
Here is a link to a helpful video explaining the node rule with the following circuit and the case where the switch has just been closed so the capacitor is not fully charged: https://youtu.be/nyYA0d7rQzE
A Mathematical Model

The node rule can be stated as:
- [math]\displaystyle{ \sum \Delta{I} = 0 }[/math]
where [math]\displaystyle{ I }[/math]stands for the current of the individual parts or wires in a circuit and the sign of the current that flows into the junction is opposite of the current that flows out of the junction. This simply supports the idea that energy cannot be created or destroyed because the total current must remain equal regardless of the path it takes. - [math]\displaystyle{ \sum_{k=1}^n I_k = 0 }[/math]
where [math]\displaystyle{ n }[/math] is the total number of branches with current flowing towards or away from the node considering the direction due to signed quantity assigned to the current. - [math]\displaystyle{ \sum_{k=1}^n \tilde{I_k} }[/math] = 0
for complex currents.
A Computational Model
This website models Kirchhoff's Laws with a simple circuit consisting of resistors and voltage sources. The generated circuit will ask for the current in one location, which can be found using Kirchhoff's Laws. The complexity of the circuit can be varied by the settings.
https://www.edumedia-sciences.com/en/media/510-kirchhoffs-circuit-laws
Examples

Simple
Question
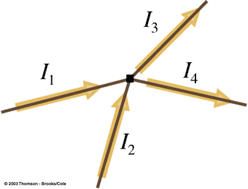
Figure 1(to the right) displays a node in a circuit. I1 is equal to 10 amps. I2 is equal to 4 amps. What is I3?
Solution
- The current flowing into the node: [math]\displaystyle{ I_1 = 10A }[/math]
The current flowing out of the node: [math]\displaystyle{ I_2 + I_3 }[/math]
We know that the current flowing in must equal the current flowing out, so [math]\displaystyle{ 10A = 4A + I_3 }[/math]
Therefore [math]\displaystyle{ I_3 }[/math] must equal 6A.
Middling
Question
In Figure 2, I1 equal 23 amps, I2 equals 5 amps and I3 equals 42 amps. What is I4?
Solution
- The current flowing into the node: [math]\displaystyle{ I_1 + I_2 = 23A + 5A = 28A }[/math]
The current flowing out of the node: [math]\displaystyle{ I_3 + I_4 = 42A + I_4 }[/math]
Applying the node rule by using substitution, [math]\displaystyle{ I_4 = -14A }[/math]
But how could we get a negative current? Getting a negative current is physically (no pun intended) impossible, but when our current comes out negative, it simply lets us know that we guessed the direction of I4 incorrectly. We assumed that the unknown current flows out instead of into the node when, in fact, the current flows into the node.
Connectedness
The Node Rule is connected to a lot of other topics in physics. The loop rule is the most important one, as the node rule and loop rule in conjunction allow us to solve circuits. The node rule is also connected to other concepts such as voltage, current and electricity. The Node Rule also supports the law of conservation of energy because in essence, current is simply the flow of electric charge, and since you cannot (at least as of now) create energy or electrons out of nothing; everything that is put into the system must come out somehow. Therefore, all the current that is applied, must come out the other end.
See the "Further Reading" section to read more on these topics.
History
Gustav Kirchhoff was a German physicist who lived during the 19th century. There are many equations and laws named after him that he helped to discover, one of them being the node rule. His circuit laws (the node rule and loop rule) were the first laws that he conceived, and he actually did this during his years in school and later wrote his doctoral dissertation on them. He created these laws in a time where electricity was a fairly new concept and was not widely used. His other achievements included coining the term "black body" radiation in 1862, which would later lead to important findings in the field of thermal radiation. In addition to his circuit laws, he is also known for his law of thermochemistry and three laws of spectroscopy, the latter of which helped lead to quantum mechanics.
Kirchhoff developed two very important rules that allow us to "solve" simple circuits, or find out different values for the different components involved in the circuit. The node rule is Kirchhoff's first rule, but there is one more, called the loop rule or Kirchhoff's Voltage Law. The loop rule states that, going around in a loop within a circuit, one will find that the voltages around the loop will sum to 0. Because voltage is just energy per unit charge, and both energy and charge are conserved, this is basically stating that no charge or energy is lost or created within the circuit.
See Also
Further Reading
External Links
https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws#Kirchhoff.27s
http://www.tutorvista.com/content/physics/physics-iv/current-electricity/kirchhoffs-rules.php
References
- Matter & Interactions 4th Edition by Ruth W. Chabay & Bruce A. Sherwood
- http://www.regentsprep.org/Regents/physics/phys03/bkirchof1/
- https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws#Kirchhoff.27s