Magnetic Field of a Long Straight Wire
Edited by Lakshana Ramanan (Fall 2025)
History
The magnetic field of a wire was first discovered during an experiment by Hans Christian Oersted (1777-1851) of Denmark in 1820. This experiment consisted of running a current through a wire and placing a compass underneath it to see if there was any effect. The effect he found changed the world forever: he had discovered the important relationship between electricity and magnetism. Before this, the world had taken note of the similarities between electricity and magnetism but nobody had truly "proved" this relationship up until this point. Oersted then went on to write his groundbreaking scientific paper "Experiments on the effect of a current of electricity on the magnetic needle," which shocked and awed the rest of the scientific world. This experiment laid the foundation for what we now study in electromagnetism courses, such as Physics II. While this finding falls directly into the category of "Magnetic Field of a Long Straight Wire," it also may very well be the most important discovery by any physicist in history (this is up for debate but this is just my opinion on the topic; nonetheless, it is extremely crucial).
Summary
A long straight wire, that is carrying some current I, will generate it's own magnetic field. The shape of the magnetic field will be concentric circles centered around the wire. The magnetic field lines are identical and the spacing of these lines increases as the distance increased. The direction of the magnetic field lines can be observed by placing small compass needles on a circle close to the wire. If there is no current, then the needles will align with the Earth's magnetic field and if there is a current, then the needles will point tangent to the circle. If the wire is vertical and the current is facing upwards, then on the left side of the wire, the magnetic field will come out towards you. On the right side of the wire, the magnetic field would go in towards the other direction. If the current was going downwards, then the magnetic field would reverse directions but would still be in concentric circles around the wire. The second form of the right hand rule in terms of the wire would be used so that the thumb is going in the direction of the current, and the fingers will go in the direction of the magnetic field. The closer you get to the wire, the stronger the magnetic field. The further you get from the wire, the weaker the magnetic field. As the magnetic field gets spread out, it is distributed over a wider circumference. The mathematical interpretation of the magnetic field is detailed below.
The Right-Hand Rule
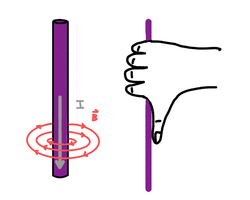
To determine the direction of the magnetic field:
- Point your thumb in the direction of conventional current I.
- Curl your fingers
- Your fingers show the direction of the magnetic field loops.
- Current upward -> field circles counterclockwise
- Current downward -> field circles clockwise
Models
Mathematical Model
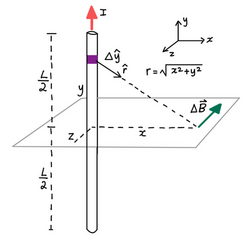
Imagine centering a wire of length [math]\displaystyle{ L }[/math] on the y-axis, and having a current [math]\displaystyle{ I }[/math] run through the wire in the +y direction. We are interested in finding the magnetic field at some point along the z axis, say [math]\displaystyle{ (0,0,z) }[/math].
From here, we use the Biot-Savart Law:
- [math]\displaystyle{ d\mathbf{B} = \frac{\mu_{0}}{4\pi} \frac{I d\mathbf{L} \times \mathbf{\hat r}}{r^2} }[/math]
In our case, [math]\displaystyle{ \mathbf{\hat r} }[/math] is simply a unit vector in the direction of a point along the wire [math]\displaystyle{ (0,y,0) }[/math] to a point along the z-axis [math]\displaystyle{ (0,0,z) }[/math]. This can be represented by:
- [math]\displaystyle{ \mathbf{\hat r} = \frac{\mathbf{r}}{|\mathbf{r}|} = \frac{(0,0,z) - (0,y,0)}{\left|(0,0,z) - (0,y,0) \right|} = \frac{(0,-y,z)}{\left|(0,-y,z)\right|} = \frac{(0,-y,z)}{\sqrt{y^2 + z^2}} }[/math]
In our case, [math]\displaystyle{ d\mathbf{L} }[/math] is simply a vector pointing along a length of the wire. Since our wire is solely along the y-axis, this can be reduced as follows:
- [math]\displaystyle{ d\mathbf{L} = d \Bigr[(0,y,0)\Bigr] = (0,dy,0) }[/math]
Now we can compute the absolute value of the cross product between [math]\displaystyle{ \mathbf{\hat r} }[/math] and [math]\displaystyle{ d\mathbf{L} }[/math], where [math]\displaystyle{ r = \sqrt{y^2 + z^2} }[/math]:
- [math]\displaystyle{ |d\mathbf{L} \times \mathbf{\hat r}| = \left|\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & -\frac{y}{r} & \frac{z}{r} \\ 0 & dy & 0 \end{vmatrix}\right| = \Biggr| \ \mathbf{i} \biggr[0 \times \left(- \frac{y}{r}\right) - \frac{z}{r} dy \biggr] - \mathbf{j} \biggr[0 - 0 \times \frac{z}{r} \biggr] + \mathbf{k} \biggr[0 \times dy - 0 \times \left(-\frac{y}{r}\right) \biggr] \ \Biggr| = \Biggr| \ \mathbf{i}\biggr[-\frac{z}{r}dy \biggr] - \mathbf{j}\biggr[0 \biggr] + \mathbf{k}\biggr[0 \biggr] \ \Biggr| = \Biggr| \ \left(-\frac{z}{r}dy,0,0\right) \ \Biggr| = \left(\frac{z}{r}dy, 0, 0\right) }[/math]
Thus we have:
- [math]\displaystyle{ d\mathbf{B} = \frac{\mu_{0}}{4\pi} \frac{I \left(\frac{z}{r}dy, 0, 0\right)}{r^2} = \frac{\mu_{0}}{4\pi} \frac{Iz}{r^3}dy = \frac{\mu_{0}}{4\pi} \frac{Iz}{(y^2 + z^2)^{3/2}}dy }[/math]
To find the total magnetic field at a point along the z-axis due to the wire, we integrate from one end of the wire to the other end of the wire, or in this case:
- [math]\displaystyle{ -\frac{L_0}{2} }[/math] to [math]\displaystyle{ \frac{L_{0}}{2} }[/math], since the wire is centered at the origin and along the y-axis.
The integral then is:
- [math]\displaystyle{ \int d\mathbf{B} = \int_{-L_0/2}^{L_0/2} \frac{\mu_{0}}{4\pi} \frac{Iz}{(y^2 + z^2)^{3/2}}dy = \frac{\mu_0}{4\pi} \frac{IL}{z\sqrt{z^2 + (L/2)^2}} }[/math]
Therefore, the total magnetic field [math]\displaystyle{ B }[/math] due to a wire of length [math]\displaystyle{ L }[/math] with current [math]\displaystyle{ I }[/math] at a distance [math]\displaystyle{ z }[/math] away from the wire is:
- [math]\displaystyle{ B = \frac{\mu_0}{4\pi} \frac{IL}{z\sqrt{z^2 + (L/2)^2}} }[/math]
Approximation
If it is known that [math]\displaystyle{ L \gt \gt z }[/math], then the denominator of the above formula can be approximated by:
- [math]\displaystyle{ \sqrt{z^2+(L/2)^2} \approx \frac{L}{2} }[/math]
Therefore, if you have a really long wire, and you are trying to find the magnetic field of a point relatively close to the rod, you can use the approximation:
- [math]\displaystyle{ B = \frac{\mu_0}{2\pi} \frac{I}{z} }[/math] [1]
In most situations, at least in the scope of this course, it is stated in the question whether or not you can use the approximation. This can come in a few different forms: "assume z<<L," "assume the length of the wire is much longer than than the distance from the wire to the observation location," etc. However, if it is not explicitly stated, a good rule of thumb is that if the length of the wire is 100 times+ the [math]\displaystyle{ z }[/math], we can use the approximation formula. Otherwise, it is smart to just play it safe and use the full formula.
GlowScript Code Example: Wire Interaction
mu0 = 4 * pi * 1e-7
wire1 = cylinder(pos=vec(0,0,-5), axis=vec(0,0,10), radius=0.05, color=color.red)
I1 = 5
radii = [0.5, 1.0, 1.5]
for r in radii:
for theta in arange(0, 2*pi, pi/12):
x = r*cos(theta)
y = r*sin(theta)
B_dir = cross(vec(x, y, 0), vec(0, 0, 1))
B_dir = B_dir.norm()
arrow(pos=vec(x, y, 0), axis=0.2*B_dir, color=color.blue)
label(pos=vec(0,2,0), text="Magnetic Field around Wire 1", box=False, height=10, color=color.black)
r_point = vec(0, 1, 0)
B_mag = (mu0 / (2*pi)) * (I1 / mag(r_point))
B_vec = cross(r_point, vec(0,0,1)).norm() * B_mag
arrow(pos=r_point, axis=0.2*B_vec.norm(), color=color.green)
label(pos=r_point + vec(0.2,0.2,0), text="B at this point", box=False, height=10, color=color.green)
wire2 = cylinder(pos=vec(1,0,-5), axis=vec(0,0,10), radius=0.05, color=color.orange)
I2 = 5
r = mag(wire2.pos - wire1.pos)
F_per_L = (mu0 / (2*pi)) * I1 * I2 / r
direction = vec(1,0,0) if I1*I2 < 0 else vec(-1,0,0)
arrow(pos=wire2.pos + vec(0,0,5), axis=0.2*direction, color=color.magenta)
label(pos=wire2.pos + vec(0.2,0,5), text="Force on Wire 2", box=False, height=10, color=color.magenta)
Magnetic Field Near a Midpoint of the Wire
Computational Model
This can be found in the mathematical model section where the infinitesimal piece is integrated. This can also be done in Glowscript as shown below:
- d = display(height=400, width=1000)
- d.background = color.white
- d.forward = vector(-0.2, -0.2, -1)
- L = 1
- d.range = 0.2 * L
- d.center = vector(0.15 * L, 0, 0)
- I = 5
- kmag = 1e-7
- N = 20
- dx = L / N
- dl = vector(dx, 0, 0)
- wire = []
- for x in arange(-L/2, L/2, dx):
c = cylinder(pos=vector(x, 0, 0), axis=dl * 0.9, radius=0.005, color=color.orange) wire.append(c)
- arr = []
- da = L/8
- for x in arange(-L/2+2*da, L/2-da, da):
- for theta in arange(0, 2*pi, pi/4):
- b = arrow(pos=vector(x,-r1*sin(theta), r1*cos(theta)), color=color.cyan,
- shaftwidth = 0.008, axis=vector(0,0,0))
- arr.append(b)
- for x in arange(-L/2+2*da, L/2-da, da):
- for theta in arange(0, 2*pi, pi/4):
- b = arrow(pos=vector(x,-r2*sin(theta), r2*cos(theta)), color=color.cyan,
- shaftwidth = 0.004, axis=vector(0,0,0))
- arr.append(b)
- b = arrow(pos=vector(x,-r2*sin(theta), r2*cos(theta)), color=color.cyan,
- for theta in arange(0, 2*pi, pi/4):
- ra = arrow(pos=vector(0,0,0), axis=vector(0,0,0), color=color.red, shaftwidth=0.005)
- dla = arrow(pos=vector(0,0,0), axis=vector(0,0,0), color=color.magenta, shaftwidth=0.005)
- dl_label = label(pos=dla.pos, text="dl", yoffset=8, xoffset=3, color=dla.color, opacity=0, box=0, line=0, height=24)
- r_label = label(pos = ra.pos + ra.axis/2, color=ra.color, text="r", yoffset=-7, xoffset=5, opacity=0, box=0, line=0, height=24)
- count = 0
- rateval = 200
- for a in arr:
- for s in wire:
- rate(rateval)
- r = a.pos - (s.pos+dl/2)
- ra.pos = (s.pos+dl/2)
- ra.axis = r
- r_label.pos = ra.pos + ra.axis/2
- dla.pos = s.pos+vector(0,0.011,0)
- dla.axis = dl
- dl_label.pos = dla.pos
- a.axis = a.axis +Bscale*kmag*I*cross(dl, norm(r))/mag(r)**2
- if count < 20:
- d.waitfor('click')
- elif count < 2*N:
- rateval = 2
- elif count < 8*N:
- rateval = 5
- elif count < 40*N:
- rateval = 50
- else:
- rateval = 100
- count = count+1
- for s in wire:
- ra.visible = False
- dla.visible = False
- r_label.visible = False
- dl_label.visible = False
Application with a Compass
If you run a current through a wire and place a compass near it, the needle of the compass deflects due to the magnetic field from this wire. With no current in the wire, the compass will face North. When approximately .314A is run through a wire, the compass deflects by approximately 20 degrees. In fact, the amount of deflection that there is from the wire can actually help you calculate the approximate magnetic field of the wire. This is because there is a particular relationship between the needle of the compass, the magnetic field of the wire, and the magnetic field of the Earth itself that looks like this:
- [math]\displaystyle{ |B_w| = |B_E| \text{tan}\theta }[/math]
The Earth itself has a magnetic field anywhere on the Earth (based on location it varies slightly, but it is easier to assume it is constant) of approximately [math]\displaystyle{ 2e^{-5} \ \text{T} }[/math] which is why the compass points notes. In the formula above, theta is the amount of degrees that, when placed directly above or underneath, the compass needle deflects from North. This is a very useful formula to have in lab or in the real world if it is unknown how much current is running through a wire.
Examples
Easy
The magnitude of the magnetic field [math]\displaystyle{ 50 \ \text{cm} }[/math] from a long, thin, straight wire is[math]\displaystyle{ 8.0 \ \text{μT} }[/math].
- a) What is the approximate current through the long wire?
- Using the approximation formula for a long, thin straight wire,
- [math]\displaystyle{ B = \frac{\mu_{0}}{4\pi}\frac{2I}{r} }[/math]
- we see the current needed to supply the stated magnetic field is:
- [math]\displaystyle{ I = \frac{4\pi r B}{2 \mu_{0}} = \frac{4\pi \times 0.5 \times 8.0 \times 10^{-6}}{2 \times 4\pi \times 10^{-7}} = 20 \ \text{A} }[/math]
- b) An ordinary compass that points north when not in the vicinity of a magnetic field is pointing at [math]\displaystyle{ \theta_{1} = 325^{°} }[/math]. A wire with a current is then placed directly above the compass and the needle now points at [math]\displaystyle{ \theta_{2} = 240^{°} }[/math]. What is the approximate magnitude of the magnetic field of this wire?
- Using our useful lab formula:
- [math]\displaystyle{ |B_{wire}| = |B_E| \text{tan}(\theta) }[/math]
- [math]\displaystyle{ \theta }[/math] will equal the difference between the initial angle and the final angle:
- [math]\displaystyle{ \theta = \theta_{2} - \theta_{1} = 240 - 325 = -85° }[/math]
- Therefore:
- [math]\displaystyle{ |B_w| = 2e^{-5} \times \text{tan}(-85°) }[/math]
- [math]\displaystyle{ |B_w| = 2.29 \times 10^{-4} \ \text{T} }[/math]
Medium
The current through a thin, straight wire that is [math]\displaystyle{ 2 \ \text{m} }[/math] long is [math]\displaystyle{ 74 \ \text{A} }[/math].
- a) What is the magnitude of the magnetic field at a location [math]\displaystyle{ 0.35 \ \text{m} }[/math] away and perpendicular to the center of the wire?
- Using the full formula:
- [math]\displaystyle{ B = \frac{\mu_0}{4\pi} \frac{LI}{z\sqrt{z^2+(L/2)^2}} }[/math]
- [math]\displaystyle{ B = \frac{\mu_0}{4\pi} \frac{2 \times 74}{0.35\sqrt{0.35^2+(2/2)^2}} }[/math]
- [math]\displaystyle{ B = 39.912 \ \mu \text{T} }[/math]
Difficult
There are two wires, separated by a distance of [math]\displaystyle{ 80 }[/math] meters on the x-axis. The left wire has a current running through it of [math]\displaystyle{ 5 \ \text{A} }[/math], while the right wire has a current running through it of [math]\displaystyle{ 12 \ \text{A} }[/math]. The length of the left wire is [math]\displaystyle{ 2 }[/math] meters, while the length of the right wire is [math]\displaystyle{ 3 }[/math] meters.
- a) Find the total magnetic field at a point on the x-axis directly in between the two wires.
- Using the full formula, the magnetic field due to the left wire is:
- [math]\displaystyle{ B_L = \frac{\mu_0}{4\pi} \frac{LI}{z\sqrt{z^2+(L/2)^2}} }[/math]
- [math]\displaystyle{ B_L = \frac{\mu_0}{4\pi} \frac{2 \times 5}{40\sqrt{40^2+(2/2)^2}} }[/math]
- [math]\displaystyle{ B_L = 6.25 \times 10^{-10} \ \text{T} }[/math]
- The magnetic field due to the right wire then is:
- [math]\displaystyle{ B_R = \frac{\mu_0}{4\pi} \frac{LI}{z\sqrt{z^2+(L/2)^2}} }[/math]
- [math]\displaystyle{ B_R = \frac{\mu_0}{4\pi} \frac{3 \times 12}{-40\sqrt{(-40)^2+(3/2)^2}} }[/math]
- [math]\displaystyle{ B_R = -2.25 \times 10^{-9} \ \text{T} }[/math]
- The total magnetic field will be the sum of the two magnetic fields:
- [math]\displaystyle{ B_T = B_L + B_R }[/math]
- [math]\displaystyle{ B_T = 6.25 \times 10^{-10} - 2.25 \times 10^{-9} }[/math]
- [math]\displaystyle{ B_T = -1.62 \times 10^{-9} \ \text{T} }[/math]
Connectedness
I am very interested in clean energy storage and production, which typically involves long wires at some point between where the energy is generated and where the electricity is used. It is important to understand all the forces involved with an electrical current, so that if something goes wrong, you can determine where the problem is and why it might be occurring so that you can fix it.
I am an Electrical Engineering major, so all of the material within this class is vastly important, not only for the following courses required for an EE major, but also for the field once we graduate and find a job. However, this concept specifically interests me because for a while I had a very difficult time finding the direction of the magnetic field in situations such as these, so this is my way of giving back in an effort to make sure future students don't run into the same problem.
I am an Industrial Engineering major and think that it is really interesting to see the theory behind how compasses are affected by currents within a wire and their associated magnetism. A compass is such an everyday item but I had never looked into why it works the way it does, and this specific topic gave me a lot of insight into that. Additionally, it is really intriguing to learn about the second form of the right hand rule and its applications.
See also
Further Reading
External Links
- Magnetic Field of a Loop
- Magnetic Field of a Disk
- Biot-Savart Law for Currents
- Magnetic Field
- Moving Point Charge
References
- Matter and Interactions Vol. II
- OpenStax University Physics
- Skulls in the Stars