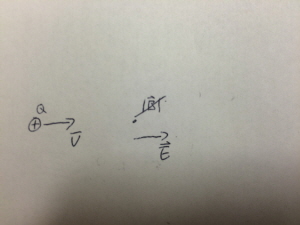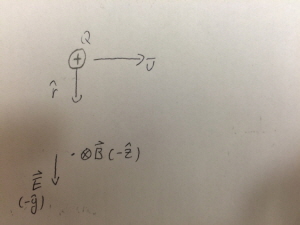Magnetic Field
Edited by Yu Jun Qin Spring 2017, Erick Phung Fall 2017
This page discusses the general properties and characteristics of magnetic fields
The Main Idea
What is a Magnetic Field?
Magnetic fields can be simply described as a field that extends through space, originating from a moving electric charge or from a magnetic dipole. This field can produce a force when acting on another magnetic object. There are many ways that a magnetic field can be generated, but the two most fundamental sources, at least for this class, are magnetic fields from a moving point charge, and magnetic fields produced from dipoles. Because magnetic fields exist across all three dimensions, magnetic fields are best represented in vector notation when doing calculations.
Magnetic Field Due to Permanent Magnet

A permanent magnet refers to any object that produces its own magnetic field. The most commonly represented permanent magnet is the bar magnet, which generate fields that emerge from one end of the bar(dubbed the North pole) and enter through the other side(dubbed the South pole). A Magnetic Dipole, such as the bar magnet, generates a magnetic field very similar to the electric field generated by a electric dipole.
Magnetic Field Due to Moving Charge
Unlike electric fields, which focus on non-mobile charges, magnetic fields are made by moving charges. Mobile charges generate an electric field perpendicular to the motion of the charge and direction of the observation location relative to the charge. Stationary charges, on the other hand, do not exert magnetic fields. In equilibrium, there is no net motion of charges inside a metal. Therefore, it should be noted that electrons inside a metal must move continuously in order to create a magnetic field. This is the very basic definition of the current, a non-equilibrium system in which there is a constant flow of electrons. Measuring electron current can be understood as counting the amount of electrons that pass through a particular cross section of a conductor. However, since it is extremely hard to count these electrons, we measure the current using other indirect methods, one being measuring the magnetic field.
Before proceeding further into the discussion, recall that we defined equilibrium above as there being no net motion of charges inside a metal. Keep in mind that equilibrium and being continuous are two totally different things.
Superposition Principle
Another property of magnetic fields is that they follow the superposition principle, which states that at a given coordinate location, the net magnetic field is simply the sum of all the magnetic fields acting on that position.
In the example on the right (click to view), the first two iterations show the magnetic field generated by two independent negative charges moving in a linear path. The third iteration with both charges moving at the same time demonstrates the additive property of the magnetic field at that location.
A Mathematical Model
The magnetic field created by a single charged particle is given by the equation [math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{q(\vec{v} \times \hat{r})}{|\vec{r}|^2} }[/math], where [math]\displaystyle{ \frac{\mu_0}{4\pi} }[/math], where [math]\displaystyle{ \frac{\mu_0}{4\pi} }[/math] is a fundamental constant equal to [math]\displaystyle{ 1 \times 10^{-7} T }[/math], [math]\displaystyle{ q }[/math] is the charge of the particle, [math]\displaystyle{ \vec{v} }[/math] is the velocity of the particle, and [math]\displaystyle{ \vec{r} }[/math] is the vector that points from source to observation location. This equation is called the Biot-Savart Law for a single moving charge.
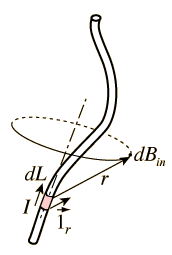
There is, however, another version of this Biot-Savart Law. This definition focuses more on the electron currents that was explained in the introductory paragraph. It is defined by [math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{I(\vec{l} \times \hat{r})}{|\vec{r}|^2} }[/math]. You may notice these equations are very similar in format. The constants and the vectors are still the same, but in this equation, [math]\displaystyle{ I }[/math] is the conventional electron current in an observed wire and [math]\displaystyle{ \vec{l} }[/math] is the length of the segment of the wire.
The Vector Cross Product
The Biot-Savart Law features the expression [math]\displaystyle{ \vec{v} \times \hat{r} }[/math]. The [math]\displaystyle{ \times }[/math] symbol does not refer to standard multiplication, but rather a form of vector multiplication called the cross product.
Given two vectors [math]\displaystyle{ \vec{a} }[/math] and [math]\displaystyle{ \vec{b} }[/math], [math]\displaystyle{ \vec{a} \times \hat{b} }[/math] calculates a third vector perpendicular to both vectors. The magnitude of this operation can be calculated as [math]\displaystyle{ \vec{a} \times \hat{b} = |a||b|\sin(\theta) }[/math]. More generally, one can find the cross product using the following formula. In the case where [math]\displaystyle{ \vec a \times \vec b = \lt ax, ay, az\gt \times \lt bx, by, bz\gt }[/math] [math]\displaystyle{ \vec a \times \vec b = \det \begin{bmatrix}\hat x & \hat y & \hat z \\ ax & ay & az \\ bx & by & bz \end{bmatrix} = \lt ay \times bz-az \times by, az \times bx-ax \times bz, ax \times by-ay \times bx\gt }[/math]
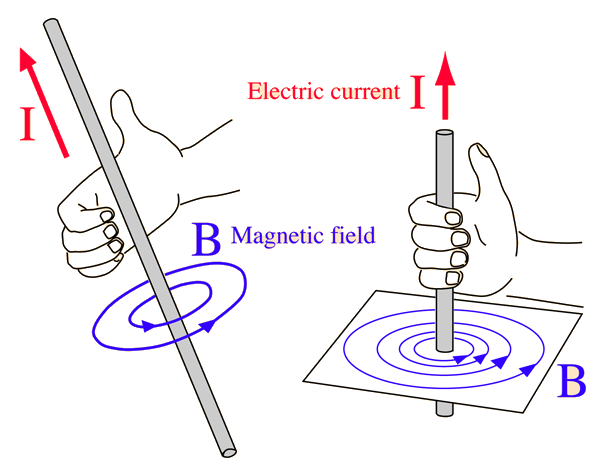
Right Hand Rule
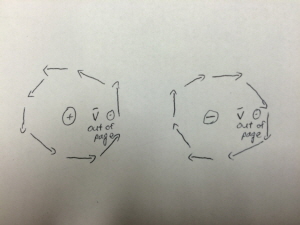
The right hand rule can be useful in determining magnetic field since it provides an easy solution to finding the direction of the field at a certain point. The technique for using the right hand rule is shown below.
 Note: All three vectors are meant to be perpendicular to each other.
Note: All three vectors are meant to be perpendicular to each other.
It is important to recognize that the direction of the magnetic field is still dependent on the sign of the charge. If you are working with a positive charge, the direction of the magnetic field is consistent with what the right hand rule states it to be. However, if you are working with a negative charge, the direction of the field is reversed.
If you apply the right hand rule in a loop around a straight wire, you find that at any given distance from the wire, the loop runs in a circle around said wire. This leads to an alternative version of the right hand rule, in which you point your thumb in the direction of the current, and your fingers will automatically curl in the direction of the field.
Magnetic Fields of Irregular Current Carrying Wires
Very often, the shape of a current carrying wire is not a straight line, which can present difficulty for anyone hoping to find the magnetic field generated by the wire. In order to remedy this, you can consider the wire as small individual parts that each contribute to the net magnetic field. By modifying the equation [math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{I(\vec{l} \times \hat{r})}{|\vec{r}|^2} }[/math], you can relate magnetic field to the position on the wire of the individual pieces. Finally, using an integral, you can add up the individual contributions of the pieces by placing the equation determined previously under the integral and using the ends of the wire as the bounds.
A Computational Model
A magnetic field produced from a moving point charge can be visualized through a VPython program utilizing code derived from the Biot-Savart Law. The gif on the right (if it does not work, try clicking on it) represents the field created by a moving proton (red sphere) at specific points around the path of the proton. This demonstrates not only the orientation of the magnetic field around the path of the proton, but also how the magnitude of the magnetic field increases as the proton approaches the observation location, and decreases as it gets farther away. The second iteration with the faster proton demonstrates that as the velocity of the proton increases, the average magnitude of the magnetic field does as well.
The Biot-Savart Law defined above can also be visualized if you click on the link below. The link sends you to a GlowScript page where you will be exposed to VPython code that animates both this law and its RHR applications. Simply click the "Run" botton at the top left of the frame to view.
<iframe src="https://trinket.io/embed/glowscript/7d28da9f50" width="100%" height="356" frameborder="0" marginwidth="0" marginheight="0" allowfullscreen></iframe>
Characteristics of the Biot-Savart Law
Single Charged Moving Particle Version
Because the equation involves the cross product of velocity and the position vector, one can find out that there is no magnetic field in the direction of the movement of the charged particle, because the cross product of two vectors in the same direction is zero.
However, even in the absence of a magnetic field, an electric field may still be present.
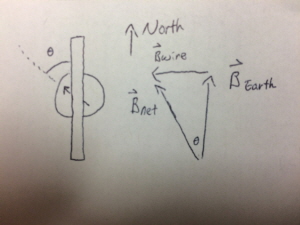
By using a compass, one can calculate the magnitude of a current. The Earth exerts a magnitude that always points to the North. When a compass is near a current with a magnetic field, the needle would be deflected by the net magnetic field. Notice that although the magnetic field of the current is perpendicular to the direction of the movement of charges, the needle is not deflected 90 degrees because of the magnetic field of the Earth, which is usually larger than that of the current. Also, because the magnetic field is exerted in a circular pattern, the direction of the magnetic field above the source is exactly the opposite of the magnetic field under the source. As a result, depending on the location of the compass, the needle may deflect in the opposite direction but with the same magnitude.
Lastly, Because of the direction of the magnetic field is influenced by the charge of the source, charge, in this case, one must pay attention to the presence of Q in the equation above.
Electric Current Version
Examples
Simple
1a. A current carrying wire running from North to South is placed on top of a compass. The current causes the compass needle to deflect 18 degrees clockwise.
Which way is the conventional current flowing?
A) North
B) East
C) South
D) West
E) No magnetic field present
Correct Answer:
Using the right hand rule, we get the answer to be C.
Middling
1b.A current carrying wire running from North to South is placed on top of a compass. The current causes the compass needle to deflect 18 degrees clockwise. The wire is located 8mm from the top of compass. What is the magnitude of the current running through the wire, given that the Earth's magnetic field is 2e-5 Tesla?
Note: Magnetic Field of a Long Straight Wire explains that a extremely long wire produces a magnetic field of [math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{2I}{|\vec{r}|} }[/math].
[math]\displaystyle{ \theta = \tan(\frac{\vec{B_of wire}}{\vec{B_of Earth}}) }[/math]
[math]\displaystyle{ \vec{B_of wire} = \vec{B_of Earth} tan(\theta) }[/math]
[math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{2I}{|\vec{r}|} }[/math].
[math]\displaystyle{ I = \frac{4\pi}{\mu_0} \frac{\vec{B_of wire}|\vec{r}|}{2I} }[/math]
Ans = 0.260A
2. A 1.2 m long wire is aligned and centered along the x axis with conventional current 9.5 A running West to East. An observation point P is located at (0.08,0.2,0) m. Calculate the magnetic field at P due to the wire between points (-0.4,0,0) m and (-0,5,0,0) m. It may help to draw a figure.
Correct Answer:
(0,0,5.92e-8) tesla
Difficult
Connectedness
1. How is this topic connected to something that you are interested in?
The concept that interests me most regarding this topic is how interrelated it is with electric charges and current. In high school, the way I was taught magnetic fields was in a way that did not emphasize its connection with electricity at all; instead we were basically taught to memorize right hand rules and just accept that magnetic fields were something that were created with current. These concepts came across as very separate entities. However, after learning more about this topic in this class, I learned why wires with current running through them create a magnetic field, and how measuring the amount of tangential magnetic field can be used to find the amount of enclosed current, among many other applications of magnetic fields.
2. How is it connected to your major?
As a biochemistry major, understanding magnetic fields is definitely not essential to any of the curriculum, but it still has useful applications. For example, some devices that we use in chem lab to identify certain compounds based on the number of specific hydrogens (nuclear magnetic resonance spectroscopy) most certainly uses magnetic fields.
3. Is there an interesting industrial application?
As a pre-med student, I am aware that many scanning technologies involved in scanning our bodies to detect any noticeable health issues also utilize magnetic fields, the most well-known probably being MRI scans to produce detailed images of different structures within the body. In an MRI scan, radio waves and powerful magnetic fields are used to obtain visuals of various organs, and this allows doctors to examine the images to see if there is anything of concern.
History
Although not studied extensively until fairly recent history, people have been aware of the existence of magnetic fields for quite some time. The only source of magnetism that people knew about was in the form of iron-rich ore called lodestones.[1]
However, at the turn of the 19th century, this began to change. In 1819, Professor Hans Christian Oersted at Copenhagen University organized a home experiment consisting of a wire with an electric current and a compass. He discovered here that every time the current was switched on, the compass needle pointed at an angle from the wire. In response to this observation made by Oersted, a French mathematician named Andre-Marie Ampere became the first to explain the relationship between electricity and magnetism. His experiments showed that two wires carrying current would attract each other if the currents flowed in the same direction, but would oppose each other if the currents flowed in the opposite direction. [2] One year later, Jean-Baptiste Biot and Félix Savart ran similar experiments and found for themselves what would become the Biot-Savart Law, a key discovery for predicting the direction of magnetic field and magnetic force in relation to electric charges.
See Also
Magnetic Field of a Long Straight Wire
External Links
https://phet.colorado.edu/en/simulation/legacy/magnet-and-compass
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magfie.html
References
https://en.wikibooks.org/wiki/Electrodynamics/Biot-Savart_Law
https://en.wikibooks.org/wiki/Electrodynamics/Magnetic_Fields
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html#c1
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/Biosav.html#c1