Magnetic Field of a Loop

Last Edited By Ava Williamson

Main Idea

Image depicting the magnetic field coming from a loop with a current.

Like other magnetic field patterns, a magnetic field can be created through motion of charge through a loop. The system is not considered to be in equilibrium, therefore there is a movement of a mobile sea of electrons, which causes an electric current in the wire. Ideal loops are considered to be perfectly circular, so for the sake of calculations, a perfectly circular loop will be used. Thus, the conventional current is directed clockwise or counterclockwise through the loop, and depending on the direction of the flow of current, the magnetic field on the axis through the center of the loop will either go in the positive or negative direction of the axis, as shown below. Formulas have been derived to assist in the calculation of these magnetic fields.

Mathematical Model

The magnetic field created by a loop is easiest to calculate on axis. This means drawing a line though the center of the loop perpendicular to the plane of the loop. This axis is commonly referred to as the "z-axis." The magnetic field is calculated by integrating across the bounds of the loop ([math]\displaystyle{ 0 }[/math] to [math]\displaystyle{ 2 \pi }[/math]), but can also be approximated with great accuracy using a derived formula. Calculation of magnetic field off of this axis is much more difficult, and usually requires the assistance of computer software. For this reason, only the calculation on axis will be addressed.

When calculating the magnitude of the magnetic field at a point on the z-axis, one can use the following formula:

[math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{(z^2 + R^2)^{3/2}} \text{ ,where R is the radius of the circular loop, and z is the distance from the center of the loop} }[/math]

This allows for the calculation of the magnitude in units of Teslas.

If the distance from the center of the loop is much greater than the radius of the loop, an approximation can be made. The formula can be simplified to:

[math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{z^3} \text{ ,where z is much greater than R} }[/math]

To provide a higher magnitude in the magnetic field, many practical applications require the addition of multiple loops to "magnify" the effect of the magnetic field. In many scenarios, electric current will run through a formation of a number of loops, [math]\displaystyle{ N }[/math], to satisfy this increasing need for a larger magnetic field. In this case, the magnitude of the induced magnetic field can be found by calculating the field produced by one loop and multiplying it by the number of loops.

This equation for the multiple loop configuration of the magnetic field of a loop will follow the equation below:

[math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{(z^2 + R^2)^{3/2}} N }[/math]

The direction of the magnetic field at a given point near the loop can be determined using the right hand rule. Point your fingers of your right hand in the direction of the conventional current, and curl them over the vector r will allow your thumb to point in the direction of the magnetic field. For example, a conventional current, I, running counterclockwise would produce a field pointing out of the page on the z-axis. This rule holds regardless of where the observational location is on the center axis.

The other version of the right-hand rule, which will help you when determining the direction of the magnetic field is as follows: The thumb of the right hand points in the direction of conventional current flow, I, and the fingers curl around in the direction of the magnetic field. The reverse is true as well, with the fingers curling in the direction of conventional current, and the thumb pointing in the direction of the magnetic field, as the right hand rule is essentially a depiction of the cross product between the two values.

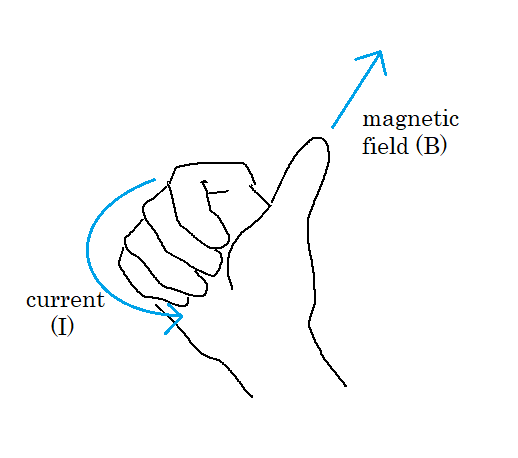
The magnetic field pattern for locations outside the ring points in the opposite direction, in accordance with the right hand rule. The right fingers still point in the direction of the current, however the observational vector perpendicular to the perimeter of the loop is now in the opposite direction. Thus, the magnetic field is in the opposite direction.

Computational Model

[Click to Run the Computational Model of the Magnetic Field produced by a Loop on Axis: https://www.glowscript.org/#/user/awilliamson40/folder/Public/program/Bfieldring]

Examples

Simple

Point [math]\displaystyle{ C }[/math] is located [math]\displaystyle{ 2 }[/math] meters away from the center of a loop of current. The loop has [math]\displaystyle{ 5 }[/math] Amps of current flowing around it and has a radius of [math]\displaystyle{ 0.1 }[/math] meters.

a) What is the magnetic field due to the loop at point C?

To solve this, all we must due is apply the main formula from the Mathematical Model:

[math]\displaystyle{ B = \frac{\mu_0}{4\pi} \frac{2\pi I R^2}{(z^2 + R^2)^{3/2}} }[/math]

We simply plug in the following values:

[math]\displaystyle{ \begin{align} z & = 2 \text{ m} \\ I & = 5 \text{ A} \\ R & = 0.1 \text{ m} \\ B & = \frac{\mu_0}{4\pi} \frac{2\pi \times 5 \times (0.1)^2}{((2)^2 + (0.1)^2)^{3/2}} \\ B & = 3.91 \times 10^{-9} \text{ T} \end{align} }[/math]

Middling

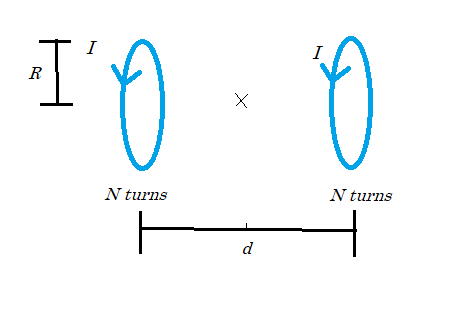
Two thin coils of radius [math]\displaystyle{ R = 2 \text{ cm} }[/math] are [math]\displaystyle{ d = 30 \text{ cm} }[/math] apart and concentric with a common z-axis. Both coils contain [math]\displaystyle{ 10 }[/math] turns of wire with a conventional current of [math]\displaystyle{ I = 2 \text{ amperes} }[/math] that runs counter-clockwise as viewed from the right side, as shown on the figure below:

a) What is the magnitude and direction of the magnetic field on the axis, halfway between the two loops, without making the approximation [math]\displaystyle{ z \gt \gt R }[/math]?

Using the right hand rule, when viewed from the right side, we know that the since current runs counter-clockwise as viewed from the right side, the magnetic field from both coils is pointing to the right. So, to calculate the magnetic field at the midpoint, we need only sum the magnetic field from each coil. To clarify, the direction of the magnetic field is to the right, or in the (+x) direction.

The magnetic field due to the left and right coils can be described as:

[math]\displaystyle{ \begin{align} B_L & = \frac{\mu_0}{4\pi} \frac{2\pi I R^2}{\left({\bigr(\frac{d}{2}}\bigr)^2 + R^2\right)^{3/2}}N = 1.45 \times 10^{-6} \text{ T} \\ B_R & = \frac{\mu_0}{4\pi} \frac{2\pi I R^2}{\left({\bigr(\frac{d}{2}}\bigr)^2 + R^2\right)^{3/2}}N = 1.45 \times 10^{-6} \text{ T}\\ \end{align} }[/math]

The sum will be:

[math]\displaystyle{ B_T = B_L + B_R = 2.9 \times 10^{-6} \text{ T} }[/math]

b) In this situation, the observation location is not very far from either coil. Calculate the magnitude of the magnetic field at the same location, using the [math]\displaystyle{ \frac{1}{z^3} }[/math] approximation.

We will use the same approach, however the useful formula is:

[math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{z^3}N }[/math]

Summing the magnetic fields again, we get:

[math]\displaystyle{ B_T = B_L + B_R = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{\left(\frac{d}{2}\right)^3}N + \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{\left(\frac{d}{2} \right)^3}N = 2.98 \times 10^{-6} \text{ T} }[/math]

Note, that since [math]\displaystyle{ z \gt \gt R }[/math], the approximate formula would be viable in this case for computing magnetic field, in an alternate problem.

c) What is the magnitude and direction of the magnetic field midway between the two coils if the current in the right loop is reversed to run clockwise?

If the current in the right loop was counterclockwise, the magnetic field at the point [math]\displaystyle{ C }[/math] would be directed in the (-x) direction, towards the left coil (determined via the right hand rule). This means that the left coil and the right coil would have opposing magnetic fields, and since they are identical coils, that would make the magnitude of the magnetic force at [math]\displaystyle{ x_{d} }[/math] [math]\displaystyle{ 0 }[/math].

Difficult

Two loops with the same current, [math]\displaystyle{ I }[/math], produce magnetic fields. Loop 1 is circular, and Loop 2 is rectangular with width [math]\displaystyle{ w }[/math] and height [math]\displaystyle{ h }[/math]. The magnetic field measured a distance [math]\displaystyle{ d }[/math] above the center Loop 1 has the same magnitude as the magnetic field measured a distance [math]\displaystyle{ d }[/math] above the center of Loop 2. You can assume that the distance [math]\displaystyle{ d }[/math] is very large compared to the dimensions of the loops. Using the dimensions provided, determine the radius [math]\displaystyle{ r }[/math] of Loop 1.

Solution:

First, It is important to recognize that the general equation

[math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{z^3} }[/math]

is the one that will be used in this problem because the distance [math]\displaystyle{ d }[/math] is very large compared to the dimensions of the loops, and it is perpendicular to the plane of the loops.

Next, Notice that the equation above can be rearranged as

[math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 I }{z^3}{(\pi R^2)} }[/math]

where [math]\displaystyle{ \pi R^2 }[/math] represents the cross sectional area of a circular loop. For a loop that is rectangular rather than circular, the cross sectional area would differ.

A more general equation for the magnetic field of a loop would read

[math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \ I A}{z^3} }[/math]

where [math]\displaystyle{ A }[/math] represents the cross sectional area of the loop.

The equation for the magnitude of the magnetic field for Loop 1 can be written as

[math]\displaystyle{ B_1 = \frac{\mu_0}{4 \pi} \frac{2 I}{d^3} {( \pi r^2 )} }[/math]

where [math]\displaystyle{ r }[/math] is the unknown constant.

The equation for the magnitude of the magnetic field for Loop 2 can be written as

[math]\displaystyle{ B_2 = \frac{\mu_0}{4 \pi} \frac{2 I}{d^3} {(w h)} }[/math]

where [math]\displaystyle{ r }[/math] is the unknown constant.

The problem states that the magnitudes of the magnetic fields are equal for a distance [math]\displaystyle{ d }[/math] above the center of each loop. This means we can set [math]\displaystyle{ B_1 = B_2 }[/math] and solve for [math]\displaystyle{ r }[/math].

[math]\displaystyle{ B_1 = B_2 }[/math]

[math]\displaystyle{ \frac{\mu_0}{4 \pi} \frac{2 I}{d^3} {( \pi r^2 )} = \frac{\mu_0}{4 \pi} \frac{2 I}{d^3} {(w h)} }[/math]

Canceling out variables, we discover

[math]\displaystyle{ r^2 = \frac{wh}{\pi} }[/math]

Leading to the final answer

[math]\displaystyle{ r = \sqrt{\frac{wh}{\pi}} }[/math]

Connectedness

Magnetic fields from electric loops are observed often in science and industrial applications. For example, a solenoid is often modeled as a bunch of loops contributing to a collective magnetic field. It is important to be able to model the field, since many scientific applications of magnetism involve circular loops. The calculations can be compared to experiments done in the lab.

This validation of theory can be extended to industrial and technological innovations seen throughout different career paths. Take, for example, the thriving CubeSat business. CubeSats are essentially miniaturized satellites (sometimes weighing between 8 and 4 kg) that perform very specific scientific missions. The payloads carried on these satellites often require a specific attitude with respect to the Earth/Sun in order to complete communications with a ground station below or to continue to receive solar power from the sun. To do this, many CubeSats often employ the use of Magnetorquer rods. These rods are essentially a solenoid (i.e. current-carrying loop with several thousand loops, [math]\displaystyle{ N }[/math]) that surrounds a metal rod (sometimes Stainless Steel). When current flows through the coils, a magnetic field is induced along the axis of the rod. The magnetic field continues to interact with the Earth's magnetic field, producing a torque on the spacecraft. When multiple magnetorquer rods are used on different axes of the spacecraft, the CubeSat can have complete control of it's attitude to continue the mission as necessary.

In all concentrations of engineering, electric and magnetic properties are important. For example, these concepts can be applied to the synthesis and manufacturing of conductors and carbon nanotubes. In many electrical experiments, it is important to understand how objects will be impacted by the creation of an induced magnetic field.

History

Hans Christian Ørsted discovered that electric currents produce a magnetic field while experimenting with currents changing the magnetic fields of nearby magnets. André-Marie Ampère found that objects with electrical currents attract each other similar to magnets, so he then hypothesized that magnetic fields are due to loops of electric current. Ampère then found that the magnetic dipole moment is essentially equal to the conventional current times the cross sectional area of a loop. The magnetic moment for a magnet was found to relate to the current in a loop in the following manner [math]\displaystyle{ \mu(magnet) = IA }[/math] where [math]\displaystyle{ A }[/math] is the cross-sectional area of the magnet.

Magnetic Field of a Loop

Contents

Last Edited By Ava Williamson

Main Idea

Mathematical Model

Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further Reading

External Links

References

Navigation menu