Superposition Principle
Claimed By: Jared Nation
The Big Picture
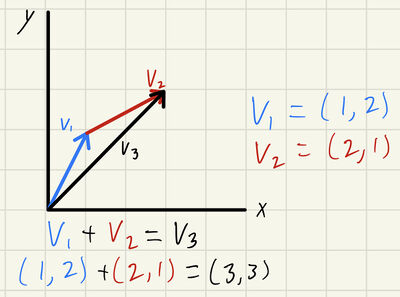
The superposition principle is based on the idea that in a closed system, an object receives a net force equal to the sum of all outside forces acting on it. This is commonly used to calculate the net electric field or magnetic field on an object. More specifically, the Superposition Principle states that the net result of multiple vectors acting on a given place and time is equal to the vector sum of each individual vector. For example, think about two waves colliding. When the waves collide, the height of the combined wave is the sum of the height of the two waves. This principle can be seen throughout nature and theory. A simple example can be seen below where Vector 3 is the sum of Vectors 1 and 2.
The Wave Model
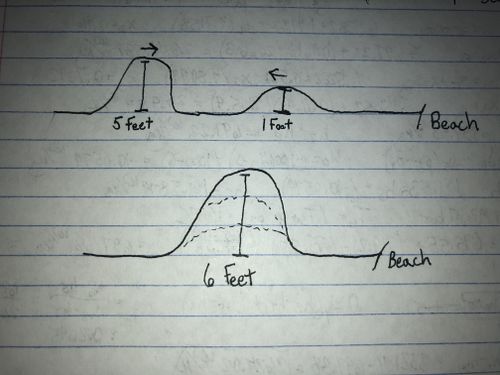
Superposition is easy to think about in the form of waves. Let's say, you are at the beach watching the ocean. A huge 5 foot wave comes towards the land and is about to crash. However, just as this happens, a smaller 1 foot tall wave forms due to the undercurrent and goes out to the ocean. Before the waves crash, they meet. At this meeting point, the combined waves become 6 feet tall (1 + 5). Why is this? This is because of superposition.
Let's now think about an orchestra. Before the concert starts, individual instruments practice on stage. Sitting in the audience, you can hear the individual instruments. However, the sound of that one instrument does not nearly compare to the sound of the entire orchestra. When the entire orchestra begins to play, the volume is much louder. This is because of the superposition principle. Each instrument produces sound waves. When an entire orchestra performs at once, the sound waves from each instrument are all summed together. The superposition principle is not only seen in waves. The superposition principle can be seen in forces, electric fields, magnetic fields, etc. However, it is easier to understand when looking at waves that everyone notices.
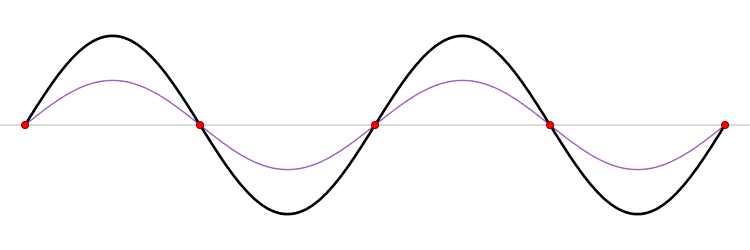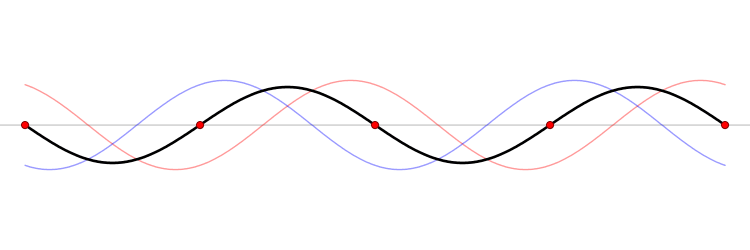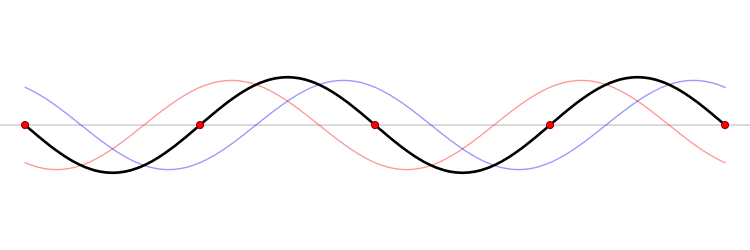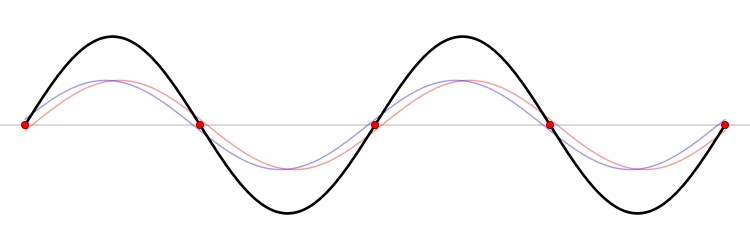
This gif depicts the superposition principle. The peaks and the troughs (the bottom of the waves) are summed together as the different waves overlap. Just as the waves of the ocean and the sound waves of the orchestra summed together, the waves in this gif sum together.
A Mathematical Model
The Superposition Principle is derived from the properties of additivity and homogeneity for linear systems which are defined in terms of a scalar value of a by the following equations:
[math]\displaystyle{ F(x_1 + x_2) = F(x_1) + F(x_2)\quad Additivity }[/math]
[math]\displaystyle{ aF(x) = F(ax)\quad Homogeneity }[/math]
The principle can be applied to any linear system and can be used to find the net result of functions, vectors, vector fields, etc. For the topic of introductory physics, it will mainly apply to vectors and vector fields such as electric forces and fields.
If given a number of vectors passing through a certain point, the resultant vector is given by simply adding all the the vectors at that point. For example, for a number of uniform electric fields passing though a single point, the resulting electric field at that point is given by:
[math]\displaystyle{ \vec{E} = \vec{E}_{1} + \vec{E}_{2} +...+ \vec{E}_{n} = \sum_{i=1}^n\vec{E}_{i} }[/math]
This same concept can be applied to electric and magnetic fields and forces. This is helpful when dealing with scenarios in which the effect that multiple point charges have on each other is in an area void of other fields. By adding together each of the contributing field vectors at a specific point, you can figure out the net contribution that all of the present charges have on the overall field experienced at that location.
You can calculate the electric field of a single point charge by using the following equation: [math]\displaystyle{ \vec{E} = \frac{1}{4 \pi \epsilon_0}\sum_{i=1}^n\frac{q_i}{r_i^2}\hat{r_i} }[/math]
Where:
[math]\displaystyle{ \frac{1}{4 \pi \epsilon_0} }[/math] is a constant that equals [math]\displaystyle{ 9e9 }[/math].
[math]\displaystyle{ q_i }[/math] is the charge of the particle you are studying. The sign of the particle matters (positive for proton, negative for electron.)
[math]\displaystyle{ r_i }[/math] is the magnitude of the distance between the particle and the observation location.
[math]\displaystyle{ \hat{r_i} }[/math] is the vector pointing from the particle to the observation location.
Conceptually, it is also important to note that an object cannot exert a force on itself, so the sum of all of the forces does not include the object itself.
Examples
When attempting to solve these problems be sure to show all steps in your solution and include diagrams whenever possible.
Simple - Two Point Charges and One Dimension
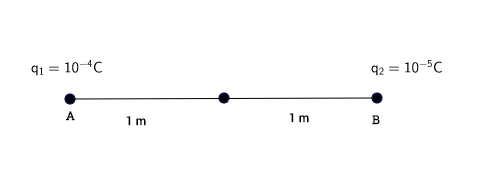
If [math]\displaystyle{ Q_1 }[/math] equals 1e-4 C and [math]\displaystyle{ Q_2 }[/math] equals 1e-5C, what is the net electric field at the midpoint of both charges?
Click for Solution
We know that the distance of each charge to the midpoint is [math]\displaystyle{ 1m }[/math]. Since this value is the magnitude of the distance it will serve as our [math]\displaystyle{ r_i }[/math] value for both of the electric field formulas.
Our [math]\displaystyle{ \hat{r_1} }[/math] value for [math]\displaystyle{ E_1 }[/math] will be [math]\displaystyle{ 1 }[/math] and the [math]\displaystyle{ \hat{r_2} }[/math] value for [math]\displaystyle{ E_2 }[/math] will be [math]\displaystyle{ -1 }[/math], if you use the midpoint as your observation point in the x-direction.
Now that we have all the necessary values to use the electric field formula, we can plug them in.
[math]\displaystyle{ \vec{E_1} = \frac{1}{4 \pi \epsilon_0}\frac{q_1}{r_1^2}\hat{r_1} = (9e9)\frac{1e-4C}{1m^2}(1m) = 9e5\frac{N}{C} }[/math]
[math]\displaystyle{ \vec{E_2} = \frac{1}{4 \pi \epsilon_0}\frac{q_2}{r_2^2}\hat{r_2} = (9e9)\frac{1e-5C}{1m^2}(-1m) = -9e4\frac{N}{C} }[/math]
At this point, you have the individual contributions of each charge. To get the net contribution of all the charges, you only need to add them.
[math]\displaystyle{ \vec{E_1}+\vec{E_2}=9e5\frac{N}{C}-9e4\frac{N}{C}= 8.1e5\frac{N}{C} }[/math]
This means that the net electric field will point towards the right with a magnitude of [math]\displaystyle{ 8.1e5\frac{N}{C} }[/math].
Medium - Three Point Charges and Two Dimensions
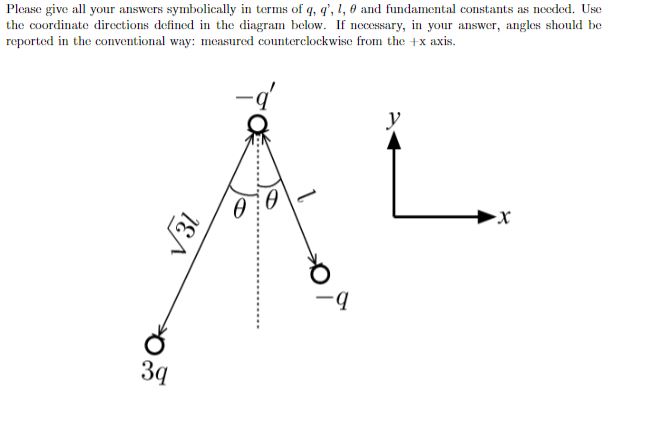
What is the magnitude of the net force on the charge -q'?
To begin, we recognize that this problem will be using the superposition principle. It is additionally important to recognize that objects can't exert forces on themselves. Keeping that in mind, the force exerted on -q' will be a combination of the forces exerted by 3q and negative q.
For this problem, let's consider -q' to be q3, 3q to be q1, and -1 to be q2 and, for the sake of simplicity, we are going to call our constant 'k'
Let's find the forces separately, then add them together:
[math]\displaystyle{ k * (q1*q3)/(r)^2 * rhat }[/math]
Now that we have the general form of the equation, we plug in variables.
[math]\displaystyle{ F1 = k * 3q(-q')/(sqrt(3) * l)^2 * (sin(theta),cos(theta),0) }[/math] [math]\displaystyle{ = k * (-q*q')/ (l^2) * (sin(theta),cos(theta),0) }[/math]
Great! Now we have the first force from q1, now we need to find the force from q2
[math]\displaystyle{ F2 = k * (q2*q3)/ (r)^2 * rhat }[/math]
[math]\displaystyle{ = k * (q*q)/(l^2) * (-sin(theta), cos(theta),0) }[/math]
Now that we've found both forces, we add them together.
[math]\displaystyle{ Fnet = F1+F2 }[/math] [math]\displaystyle{ = k * (-q*q')/ (l^2) * (sin(theta),cos(theta),0) + k * (q*q)/(l^2) * (-sin(theta), cos(theta),0) }[/math] [math]\displaystyle{ = k * (q*q')/(l^2) * (-2sin(theta),0,0) }[/math]
Once we were able to recognize our problem, it became as simple as plugging in variables and using algebra to solve the problem.
Additionally, if we were asked "What is the direction of the force on the charge -q'?"
Looking back at our work, we can see that our vertical components cancel out, leaving [math]\displaystyle{ -2sin(theta) }[/math] Indicating our direction is negative x.
We could get to this conclusion without looking at the math by understanding that electric field falls off in a way that resembles [math]\displaystyle{ 1/(r)^2 }[/math]
For q1, it is sqrt(3) times farther than q2, and 3 times the charge. Which is equivalent to [math]\displaystyle{ 3*q/(sqrt(3))^2 }[/math] Which is equivalent to q2 in the vertical direction. In the horizontal direction, q2 is slightly closer, meaning that the total net charge should be in the negative x direction.
Medium - Two Point Charges and Two Dimensions
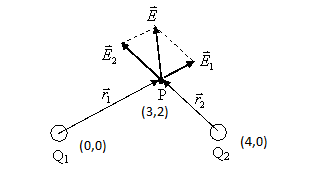
If [math]\displaystyle{ Q_1 }[/math] and [math]\displaystyle{ Q_2 }[/math] are positive point charges with a charge of e, what is the net electric field at point P?
Click for Solution
To begin this problem, the first step is to find [math]\displaystyle{ r_1 }[/math] and [math]\displaystyle{ r_2 }[/math], the vectors from the charges to point P as well as their magnitudes:
[math]\displaystyle{ \vec{r_1} = 3\hat{i}+2\hat{j}-(0\hat{i}+0\hat{j})\Rightarrow\vec{r_1} = 3\hat{i}+2\hat{j} }[/math]
[math]\displaystyle{ ||\vec{r_1}|| = \sqrt{3^2 + 2^2} =\sqrt{13} }[/math]
[math]\displaystyle{ \vec{r_2} = 3\hat{i}+2\hat{j}-(4\hat{i}+0\hat{j})\Rightarrow\vec{r_2} = -1\hat{i}+2\hat{j} }[/math]
[math]\displaystyle{ ||\vec{r_2}|| = \sqrt{-1^2 + 2^2} =\sqrt{5} }[/math]
Using these in the equation for an electric field from a point charge, you get:
[math]\displaystyle{ \vec{E_1} = \frac{1}{4 \pi \epsilon_0}\frac{Q_1}{||r_1||^2}\hat{r_1}=\frac{1}{4 \pi \epsilon_0}\frac{e}{13}\lt \frac{3}{\sqrt{13}}\hat{i}+\frac{2}{\sqrt{13}}\hat{j}\gt = \lt 9.21E-11\hat{i}+6.14E-11\hat{j}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_2} = \frac{1}{4 \pi \epsilon_0}\frac{Q_2}{||r_2||^2}\hat{r_2}=\frac{1}{4 \pi \epsilon_0}\frac{e}{5}\lt \frac{-1}{\sqrt{5}}\hat{i}+\frac{2}{\sqrt{5}}\hat{j}\gt = \lt -1.29E-10\hat{i}+2.58E-10\hat{j}\gt }[/math]N/C
Then, simply add the two electric fields together:
[math]\displaystyle{ \vec{E}=\vec{E_1}+\vec{E_2} = \lt -3.69E-11\hat{i}+3.19E-10\hat{j}\gt }[/math]
Difficult - Five Point Charges and Three Dimensions
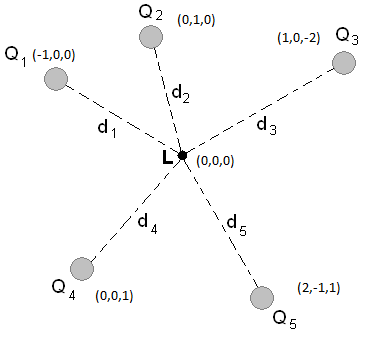
If all point charges have a charge of e, what the the net electric field present at point L?
Click for Solution
This problem is similar to the previous examples but this one includes the z axis and more points. Since there are 5 points and you have already had some practice, you will only see the procedure for the first one. We will still work through the whole problem. Again, first each vector and magnitude:
[math]\displaystyle{ \vec{d_5} = 0\hat{i}+0\hat{j}+0\hat{k}-(2\hat{i}-1\hat{j}-1\hat{k})-\Rightarrow\vec{d_5} = -2\hat{i}+1\hat{j}+1\hat{k} }[/math]
[math]\displaystyle{ ||\vec{d_5}|| = \sqrt{(-2)^2 + 1^2 + 1^2} = 2 }[/math]
Do the same for each of the other point charges and plug them into the electric field formula:
[math]\displaystyle{ \vec{E_5} = \frac{1}{4 \pi \epsilon_0}\frac{Q_5}{||d_5||^2}\hat{d_5}=\frac{1}{4 \pi \epsilon_0}\frac{e}{4}\lt \frac{-2}{2}\hat{i}+\frac{1}{2}\hat{j}+\frac{1}{2}\hat{k}\gt = \lt -3.6E-10\hat{i}+1.8E-10\hat{j}+1.8E-10\hat{k}\gt }[/math]N/C
Follow the same steps for the other electric fields and add them all together to get your final answer:
[math]\displaystyle{ \vec{E_1} = \lt 1.44E-9\hat{i}+0\hat{j}+0\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_2} = \lt 0\hat{i}-1.44E-9\hat{j}+0\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_3} = \lt -1.29E-10\hat{i}+0\hat{j}+2.58E-10\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_4} = \lt 0\hat{i}+0\hat{j}-1.44E-9\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E} = \vec{E_1}+\vec{E_2}+\vec{E_3}+\vec{E_4}+\vec{E_5}=\lt 9.51E-10\hat{i}-1.26E-9\hat{j}+1.00E-9\hat{k}\gt }[/math]N/C
Connectedness
The superposition principle is critical as you progress to more complicated topics in Physics. This principle simplifies many topics that you will encounter further ahead, by assuming that their net contribution will be equal to the addition of all the individual ones. You will use superposition with electric fields and forces, as well as magnetic fields and forces. In addition, if in a problem you are only given the final net contribution of any type of field, you can inversely solve it by constructing equations that relate the individual formulas. You can then plug in values, and subtract in order to find the magnitudes of each individual contributor. This will also enable you to better analyze different types of circuits.
However, the superposition principle also aids outside of the world of abstract electromagnetism. It is also useful for static problems, which you might encounter if you are a Civil or Mechanical Engineer, or systems and circuitry, which you might encounter if you are a Biomedical engineer.
History
The superposition principle was supposedly first stated by Daniel Bernoulli. Bernoulli was a famous scientist whose primary work was in fluid mechanics and statistics. If you recognize the name, he is primarily remembered for discovering the Bernoulli Principle. In 1753, he stated that, "The general motion of a vibrating system is given by a superposition of its proper vibrations." This idea was at first rejected by some other popular scientists until it became widely accepted due to the work of Joseph Fourier. Fourier was a famous scientist known for his work on the Fourier Series, which is used in heat transfer and vibrations, as well as his discovery of the Greenhouse Effect. Fournier’s support legitimized Bernoulli’s claims and has made a huge impact on history.
See also
Next Topics
Now that you have a solid understanding of the Superposition Principle, you can move on to these topics:
Further reading
Books, Articles or other print media on this topic
Schrodingers' Cat from a Superposition Point of View
External Links
Visual Explanation of Superposition in Electric Fields
Electric Fields and Superposition Principle Crash Course Video
Instructional video on how to calculate the net electric field using the superposition principle
Additional Video on calculating superposition principle
Using superposition principle to analyze solar cells