Inclined Plane

The Main Idea

An inclined plane is a flat surface that is higher on one end than the other... a real life right-triangle. Inclined planes are commonly used to move objects to a higher or lower place. These slopes lessen the force needed to move an object, but do require the object to be moved a greater distance, the hypotenuse of the triangular plane. Some examples of inclined planes include ramps, stairs, wedges (such as a door stopper), or even mountains which people sled down. To understand the motion of something moving along an inclined plane, forces may be taken into account using Newton's Laws, or the energy principle could be used if the object is moving or has a rotation.

A Mathematical Model

To obtain a mathematical model using Newton's Laws for an object on an inclined plane, it is easiest to construct a free body diagram with the object as the system. This figure showcases an example free body diagram. Most of the forces that could act on an inclined plane are shown. Depending on the question, all may or may not be present, especially friction.

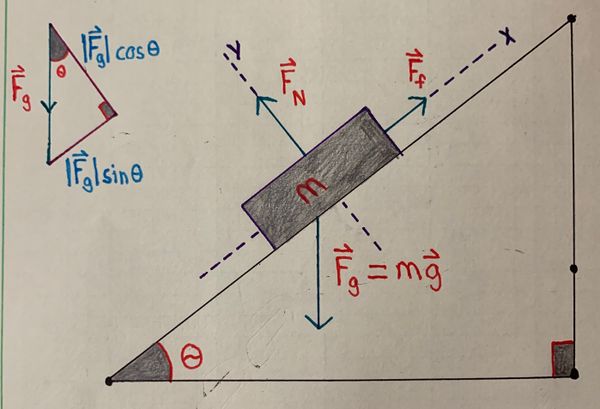
A Representation for the Mathematical Model

It is important to understand the forces that act on an object traveling on an inclined plane. For example, the three forces acting here are the force of gravity, the normal force, and the force of friction. However, imagine if an object was moving up a frictionless inclined plane. Clearly, it would eventually slow down, stop, and begin moving back down the plane. This is because of the force of gravity. While the force of gravity only acts in the -y direction, it can be broken down into its x and y components to show that it has some sort of effect on the object moving up the inclined plane in the x-direction opposite to its movement. If it did not, then the object would keep rolling upwards forever.

Variables:

[math]\displaystyle{ \theta = }[/math] Angle between the hypotenuse of the inclined plane and the horizontal

[math]\displaystyle{ \mathbf{F_g} = }[/math] The gravitational force on the object

[math]\displaystyle{ m g \ \text{sin}\theta = }[/math] A component force of gravity parallel to the plane (if [math]\displaystyle{ m g \ sinθ \gt |\mathbf{F_f}| }[/math] the body slides down the plane)

[math]\displaystyle{ m g \ \text{cos}\theta = }[/math] A component force of gravity acting into the plane (opposite to [math]\displaystyle{ F_N }[/math])

[math]\displaystyle{ \mathbf{g}= }[/math] The acceleration due to gravity

[math]\displaystyle{ m = }[/math] The mass of the object

[math]\displaystyle{ F_N = }[/math] The normal force (perpendicular to the plane)

[math]\displaystyle{ F_f = }[/math] The frictional force of the inclined plane (sometimes it is omitted)

Equations:

[math]\displaystyle{ \mathbf{F_{net}} = \sum \mathbf{F} = \sqrt{{F_x}^2 + {F_y}^2} }[/math], where the x and y axes are as shown in the image.

Note that [math]\displaystyle{ F_y }[/math] tends to be [math]\displaystyle{ 0 }[/math], so [math]\displaystyle{ \mathbf{F_{net}} = \sqrt{{F_x}^2} = F_x }[/math]

[math]\displaystyle{ F_x = F_f - F_{g_x} = F_f - mg \ \text{sin}\theta }[/math]

[math]\displaystyle{ F_y = F_N - F_{g_y} = F_N - mg \ \text{cos}\theta }[/math]

A Computational Model

Using GlowScript or VPython, we are able to model a box on an inclined plane moving upward with an initial velocity, then pulled downward as it is being affected by gravity. This code allows us to observe the final velocity, position, speed, and acceleration of the box.

Code

from __future__ import division from visual import * from visual.graph import *

scene.title = "Incline Plane"

scene.background = color.black scene.center = (0.7, 1, 0) # location at which the camera looks

inclinedPlane = box(pos = vector(0.6, 0, 0), size = (1.2, 0.02, 0.2), color = color.green, opacity = 0.3)

cart = box(size = (0.2, 0.06, 0.06), color = color.blue) # 20-cm long cart on the inclined plane

trail = curve(color = color.yellow, radius = 0.01) # units are in meters

cart.m = 0.5 # mass of cart in kg

cart.pos = vector(0, 0.04, 0.08)

cart.v = vector(0, 0, 0) # initial velocity of car in (vx, vy, vz) form, units are m/s

theta = 25.0 * (pi / 180.0)

inclinedPlane.rotate(angle = theta, origin = (0, 0, 0), axis = (0,0,1)) cart.rotate(angle = theta, origin = (0, 0, 0), axis = (0,0,1))

cart.v = norm(inclinedPlane.axis) cart.v.mag = 3

g = 9.8 # acceleration due to gravity; units are m/s/s

mu = 0.20 # coefficient of friction between cart and plane

t = 0 #starting time deltat = 0.0005 # time step units are s

print "initial cart position (m): ", cart.pos

while cart.pos.y > 0.02 :

   rate(1000)    
   Fnet = norm(inclinedPlane.axis)
   
   Fnet.mag = -(cart.m * g * sin(theta))
   
   if cart.v.y > 0:
       Fnet.mag += (mu * cart.m * g * cos(theta))
   else:
       Fnet.mag -= (mu * cart.m * g * cos(theta))
   
   cart.v = cart.v + (Fnet/cart.m * deltat)

   cart.pos = cart.pos + cart.v * deltat

   trail.append(pos = cart.pos)
  
   t = t + deltat

print "final time (s): ", t print "final cart position (m): ", cart.pos print "final cart velocity (m/s): ", cart.v print "final cart speed (m/s): ", mag(cart.v) print "final cart acceleration (m/s/s): ", (mag(Fnet) / cart.m)

Examples

The easiest example of an object on an inclined plane is removing all forces, except gravity. Since gravity is the only force acting on the object, the computations are much easier. To make inclined plane problems harder, adding more forces, such as friction, or calculating for factors other than net force can be included, such as finding the acceleration or time it takes for the block to go from the top to the bottom of an inclined plane. As well, adding in rotation, with a ball rolling down the plane, would demonstrate other difficulties.

Simple

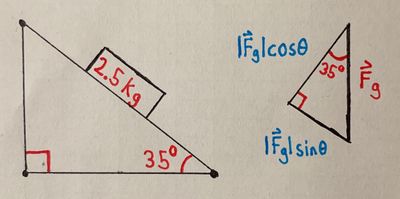
A [math]\displaystyle{ 2.5 \ kg }[/math] block slides down an inclined plane inclined with an angle of [math]\displaystyle{ 35^\text{o} }[/math] to the horizontal. The coefficient of kinetic friction ([math]\displaystyle{ \mu_{k} }[/math]) is [math]\displaystyle{ 0.14 }[/math].

a) Draw a free-body diagram for the block. If needed, refer to Free Body Diagram for help.

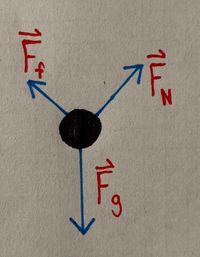
b) Determine the normal force ([math]\displaystyle{ F_N }[/math]) exerted on the block:

Using the free body diagram and our Mathematical Model, we see that the normal force must be equal in magnitude and opposite in direction of the y-component of the gravitational force:

[math]\displaystyle{ F_N = |\mathbf{F_g}| \ \text{cos}(\theta) }[/math]

Plugging in values gives:

[math]\displaystyle{ F_N = mg \ \text{cos}(35^\text{o}) = 2.5 \times 9.81 \times \text{cos}(35^\text{o}) }[/math]

Which is equal to:

[math]\displaystyle{ F_N = 20.09 \ \text{Newtons} }[/math]

c) Determine the force of kinetic friction ([math]\displaystyle{ F_f }[/math]):

It is known that the force of friction is directly proportional to the normal force:

[math]\displaystyle{ F_f = \mu_k F_N }[/math]

Plugging in values gives:

[math]\displaystyle{ F_f = 0.14 \times 20.09 }[/math]

Which is equal to:

[math]\displaystyle{ F_f = 2.81 \ \text{Newtons} }[/math]

d) Determine the acceleration of the block:

It can be reasoned that the acceleration must only be in the x-direction, due to the block not falling through the inclined plane. Therefore, we will only consider the acceleration along the x-axis.

We begin by stating that the forces along the x-axis must add to equal the block's mass times its acceleration along the x-axis:

[math]\displaystyle{ F_x = |\mathbf{F_g}| \ \text{sin}(\theta) + (-F_f) = ma_x }[/math]

Simplifying for [math]\displaystyle{ a_x }[/math] gives:

[math]\displaystyle{ a_{net_x} = \frac{|\mathbf{F_g}| \ \text{sin}(\theta) - F_f}{m} }[/math]

Plugging in values gives:

[math]\displaystyle{ a_{net_x} = \frac{(2.5 \times 9.81 \times \ \text{sin}(35^\text{o})) - 2.81}{2.5} }[/math]

Which equals:

[math]\displaystyle{ a_{net_x} = 4.5 \ \frac{m}{s^2} }[/math]

Middling

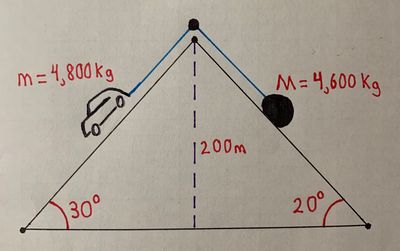
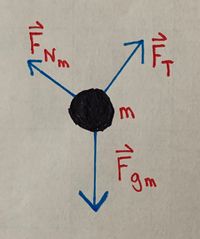
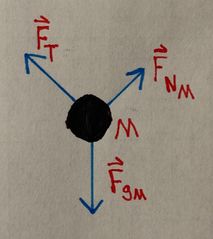
The figure shows a [math]\displaystyle{ 4800 }[/math] kg car ([math]\displaystyle{ m }[/math]) descending on one side of a hill that has an angle of [math]\displaystyle{ 30^\text{o} }[/math] with the the ground. A counterweight of mass [math]\displaystyle{ 4600 }[/math] kg ([math]\displaystyle{ M }[/math]), on the other side of the hill, helps the car's breaks slow the vehicle down. The rolling friction of both the car and the counterweight are negligible.

a) Draw Free Body Diagrams for the car ([math]\displaystyle{ m }[/math]) and the counterweight ([math]\displaystyle{ M }[/math]):

b) How much braking force ([math]\displaystyle{ F_{brakes} }[/math]) does the car need to descend at a constant speed?

First, since we know the car has no net acceleration along y-axis (it is not speeding into the inclined plane or lifting off), we know the x-component (parallel to the inclined plane) of the net acceleration ([math]\displaystyle{ a_{net_x} }[/math]) is what we need to analyze. Furthermore, since we want the car to descend at constant speed, we know that [math]\displaystyle{ a_{net_x} }[/math] must be equal to [math]\displaystyle{ 0 }[/math]:

[math]\displaystyle{ a_{net_x} = 0 }[/math]

Next, we set up force equations using Newton's Second Law and our free body diagrams, taking the positive x-direction to be the car going down the inclined plane. Keep in mind the coordinate plane we have established sort of curves along the inclined plane and tension, so that the positive x-direction for the counterweight is up the hill.

For the car, the net force along the x-axis ([math]\displaystyle{ F_{net_{x_m}} }[/math]), where [math]\displaystyle{ \theta }[/math] is used to represent the angle between the horizontal and the hypotenuse of the inclined plane ([math]\displaystyle{ 30^\text{o} }[/math]), is:

[math]\displaystyle{ F_{net_{x_m}} = |\mathbf{F_{g_m}}| \ \text{sin}(\theta) + (-F_T) + (-F_{brake}) }[/math]

For the counterweight, the net force along the x-axis ([math]\displaystyle{ F_{net_{x_M}} }[/math]), where [math]\displaystyle{ \phi }[/math] is used to represent the angle between the horizontal and the hypotenuse of the inclined plane ([math]\displaystyle{ 20^\text{o} }[/math]), is:

[math]\displaystyle{ F_{net_{x_M}} = (-|\mathbf{F_{g_M}}| \ \text{sin}(\phi)) + F_T }[/math]

Note that the force of tension is the same but in opposite directions for the two objects in our system.

Furthermore, note that the accelerations of the car and counterweight must be the same, as long as the rope does not break and is held taut. We also want [math]\displaystyle{ 0 }[/math] acceleration along the x-axis. Therefore:

[math]\displaystyle{ F_{net_{x_m}} = |\mathbf{F_{g_m}}| \ \text{sin}(\theta) + (-F_T) + (-F_{brake}) = ma_x = 0 }[/math]

[math]\displaystyle{ F_{net_{x_M}} = (-|\mathbf{F_{g_M}}| \ \text{sin}(\phi)) + F_T = Ma_x = 0 }[/math]

Adding these two equations together allows for the cancellation of [math]\displaystyle{ F_T }[/math], which greatly simplifies things, so let us do that:

[math]\displaystyle{ F_{net_{x_m}} + F_{net_{x_M}} = (|\mathbf{F_{g_m}}| \ \text{sin}(\theta) + (-F_T) + (-F_{brake})) + ((-|\mathbf{F_{g_M}}| \ \text{sin}(\phi)) + F_T) = ma_x + Ma_x = 0 }[/math]

Which equals:

[math]\displaystyle{ F_{net_{x_m}} + F_{net_{x_M}} = (F_T - F_T) + (|\mathbf{F_{g_m}}| \ \text{sin}(\theta) - |\mathbf{F_{g_M}}| \ \text{sin}(\phi)) - F_{brakes} = (M+m)a_x = 0 }[/math]

Thus, we see that the needed breaking force is equal to the difference between the car's x-component of the gravitational force and the counterweight's x-component of the gravitational force, which physically makes sense:

[math]\displaystyle{ |\mathbf{F_{g_m}}| \ \text{sin}(\theta) - |\mathbf{F_{g_M}}| \ \text{sin}(\phi) = F_{brakes} }[/math]

Plugging in variables gives:

[math]\displaystyle{ F_{brakes} = mg \ \text{sin}(30^\text{o}) - Mg \ \text{sin}(20^\text{o}) }[/math]

And plugging in values gives:

[math]\displaystyle{ F_{brakes} = (4800 \times 9.81 \times \ \text{sin}(30^\text{o})) - (4600 \times 9.81 \times \ \text{sin}(20^\text{o})) }[/math]

Which equals:

[math]\displaystyle{ F_{brakes} = 8110 \ \text{Newtons} }[/math]

Difficult

Part I

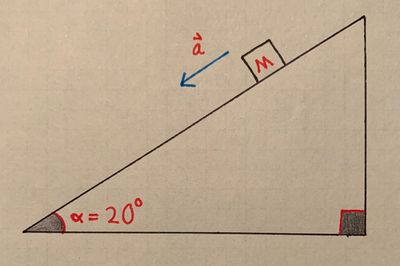
A block of mass [math]\displaystyle{ M = 10 \ \text{kg} }[/math] starts traveling down an inclined plane at time [math]\displaystyle{ t = 5 }[/math] seconds. The angle between the inclined plane and the horizontal is [math]\displaystyle{ \alpha = 20^\text{o} }[/math]. There is an applied force [math]\displaystyle{ F_A = \frac{10}{t^2} + Mt^2 }[/math] working with the motion of the block (down the inclined plane). Also, consider the effect of friction, with a coefficient of kinetic friction [math]\displaystyle{ \mu_k = 0.23 }[/math].

a) Draw a Free Body Diagram for the block:

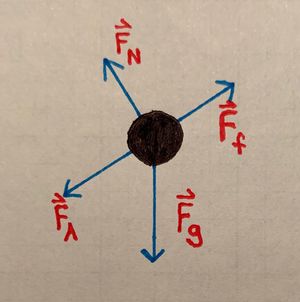
b) Find the time-dependent solution of [math]\displaystyle{ \mathbf{a_{net}} }[/math]:

Using our free body diagram and some intuition, we can reason that the net force along the y-axis ([math]\displaystyle{ F_y }[/math]) is [math]\displaystyle{ 0 }[/math], since the only motion is along the x-axis. Therefore, we will only analyze the net force along the x-axis ([math]\displaystyle{ F_x }[/math]). By using Newton's Second Law, we can find the acceleration along the x-axis ([math]\displaystyle{ a_x }[/math])

[math]\displaystyle{ F_y = 0 }[/math]

[math]\displaystyle{ F_x = \sum F = Ma_x }[/math]

It will be useful to go ahead and describe all the forces working on the block, namely the force of gravity ([math]\displaystyle{ F_g }[/math]), the normal force ([math]\displaystyle{ F_N }[/math]), the force of friction ([math]\displaystyle{ F_f }[/math]), and the applied force ([math]\displaystyle{ F_A }[/math]):

[math]\displaystyle{ F_g = Mg = 98.1 \ \text{Newtons} }[/math]

[math]\displaystyle{ F_N = F_g \text{cos}(\alpha) = Mg \times \text{cos}(\alpha) = 10 \times 9.81 \times \text{cos}(20^\text{o}) = 92.18 \ \text{Newtons} }[/math]

[math]\displaystyle{ F_f = \mu_k F_N = \mu_k \times Mg \times \text{cos}(\alpha) = 0.23 \times 10 \times 9.81 \times \text{cos}(20^\text{o}) = 21.2 \ \text{Newtons} }[/math]

[math]\displaystyle{ F_A = \frac{10}{t^2} + Mt^2 = \frac{10}{t^2} + 10t^2 = 10\left(\frac{1}{t^2} + t^2 \right) }[/math]

Now summing the forces above that are along the x-axis, we get:

[math]\displaystyle{ F_x = (F_g \text{sin}(\alpha)) + (F_A) - (F_f) = Ma_x }[/math]

Simplifying gives:

[math]\displaystyle{ F_x = (Mg \times \text{sin}(20^\text{o})) + \left(10\left(\frac{1}{t^2} + t^2\right)\right) - ( \mu_k \times Mg \times \text{cos}(20^\text{o})) }[/math]

Which equals:

[math]\displaystyle{ F_x = 10\left(\frac{1}{t^2} + t^2\right) + 12.35 }[/math]

Therefore the time-dependent solution of [math]\displaystyle{ a_x }[/math] is:

[math]\displaystyle{ a_x(t) = \frac{F_x}{M} = \left(\frac{1}{t^2} + t^2\right) + 1.235 \ \left( \frac{m}{s^2} \right) }[/math]

c) Given that the velocity of the block at [math]\displaystyle{ t = 5 }[/math] seconds ([math]\displaystyle{ v(5) }[/math]) is [math]\displaystyle{ 0 \ \frac{m}{s} }[/math], what will the block's velocity be at [math]\displaystyle{ t = 10 }[/math] seconds ([math]\displaystyle{ v(10) }[/math])?

It is well known from calculus that if you integrate a rate with respect to time, then you can find the amount that the rate describes has changed. Since acceleration is the rate of change of the velocity, integrating the acceleration we have found with respect to time will give the velocity at time [math]\displaystyle{ t = 10 }[/math] seconds:

[math]\displaystyle{ \int a_x(t) \ dt = v_x(t) + C }[/math]

If we can integrate [math]\displaystyle{ a_x(t) }[/math] with respect to time, then we will be able to analytically write down [math]\displaystyle{ v(10) }[/math]:

[math]\displaystyle{ \int a_x(t) \ dt = \int \left(\frac{1}{t^2} +t^2 + 1.235\right) \ dt }[/math]

Rewriting this as:

[math]\displaystyle{ \int \left(\frac{1}{t^2} +t^2 + 1.235\right) \ dt = \int (t^{2} + t^{-2} + 1.235) \ dt }[/math]

Makes it easy to see that the antiderivative will be:

[math]\displaystyle{ \int (t^{2} + t^{-2} + 1.235) \ dt =\frac{t^3}{3} - \frac{1}{t} + 1.235t + C }[/math]

Therefore:

[math]\displaystyle{ v_x(10) = \frac{10^3}{3} - \frac{1}{10} + 1.235 \times 10 + C = 345.58 + C }[/math]

Taking into account [math]\displaystyle{ v_x(5) = 0 }[/math], we can find [math]\displaystyle{ C }[/math].

[math]\displaystyle{ 0 = 47.64 + C }[/math]

Therefore [math]\displaystyle{ C = -47.64 }[/math] and:

[math]\displaystyle{ v_x(10) = 345.58 - 47.64 = 297.94 \ \frac{m}{s} }[/math]

Part II

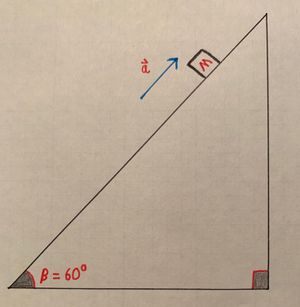
At time [math]\displaystyle{ t = 10 }[/math] seconds, the block reaches another inclined plane. This inclined plane's angle to the horizontal is [math]\displaystyle{ \beta = 60^\text{o} }[/math]. A new applied force [math]\displaystyle{ F_A = t^2(10t - 5) }[/math] works AGAINST the motion of the block, until its velocity ([math]\displaystyle{ v_x }[/math]) is [math]\displaystyle{ 0 \ \frac{m}{s} }[/math]. The force of friction still works against the motion of the block with a new coefficient of friction [math]\displaystyle{ \mu_k = 0.40 }[/math].

a) Draw a Free Body Diagram for the block:

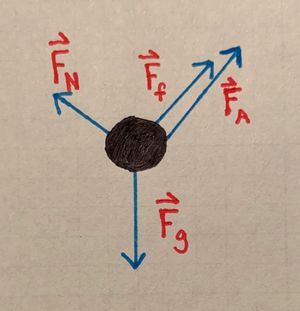
b) Find the time-dependent solution of [math]\displaystyle{ \mathbf{a_{net}} }[/math]:

To find [math]\displaystyle{ \mathbf{a_{net}} }[/math], it will be useful to recognize that [math]\displaystyle{ F_y }[/math] will be [math]\displaystyle{ 0 }[/math]. Therefore, we only need to analyze [math]\displaystyle{ F_x }[/math] to find [math]\displaystyle{ a_x(t) }[/math], and thus [math]\displaystyle{ \mathbf{a_{net}} }[/math].

It will also be useful to write down each of the forces acting on the block. Referring to the free body diagram, we have:

[math]\displaystyle{ F_g = Mg = 10 \times 9.81 = 98.1 }[/math]

[math]\displaystyle{ F_N = F_g \ \text{cos}(\beta) = Mg \times \text{cos}(\beta) = 10 \times 9.81 \times \text{cos}(60^\text{o}) = 49.05 }[/math]

[math]\displaystyle{ F_f = \mu_k F_N = \mu_k \times Mg \times \text{cos}(\beta) = 0.40 \times 49.05 = 19.62 }[/math]

[math]\displaystyle{ F_A = t^2(10t - 5) }[/math]

Summing the forces that work along the x-axis and keeping in mind that the applied force works against the direction of motion, we get:

[math]\displaystyle{ F_x = F_g \ \text{sin}(\beta) - F_A - F_f = Ma_x }[/math]

Plugging in values gives:

[math]\displaystyle{ F_x = 84.96 - t^2(10t - 5) - 19.62 }[/math]

Which simplifies to:

[math]\displaystyle{ F_x = 65.34 - t^2(10t - 5) }[/math]

Therefore:

[math]\displaystyle{ a_x(t) = \frac{F_x}{M} = 6.534 - t^2(t - 0.5) }[/math]

c) At what time [math]\displaystyle{ t_\text{o} }[/math] seconds, is the velocity ([math]\displaystyle{ v_{t_\text{o}} }[/math]) of the block [math]\displaystyle{ 0 \ \frac{m}{s} }[/math]?

The approach to this question will be very similar to the approach of Part I's part c). We will find the antiderivative of the [math]\displaystyle{ a_x(t) }[/math] we found in part b):

[math]\displaystyle{ \int a_x(t) \ dt = v_x(t) + C }[/math]

To find the antiderivative, we make the following simplification to the integrand:

[math]\displaystyle{ 6.534 - t^2(t - 0.5) = 6.534 - t^3 + 0.5t^2 }[/math]

It is easy to see that the antiderivative is:

[math]\displaystyle{ \int (6.534 - t^3 + 0.5t^2) \ dt = 6.534t - \frac{t^4}{4} + \frac{t^3}{6} + C }[/math]

Since [math]\displaystyle{ v_x(10) }[/math] must equal [math]\displaystyle{ 297.94 \ \frac{m}{s} }[/math], we have:

[math]\displaystyle{ 297.94 = 6.534 \times 10 - \frac{10^4}{4} + \frac{10^3}{6} + C }[/math]

Therefore, [math]\displaystyle{ C }[/math] must equal:

[math]\displaystyle{ C = 297.94 - 65.34 + 2500 - \frac{1000}{6} = 2565.93 }[/math]

Now we set [math]\displaystyle{ v_x(t_\text{o}) }[/math] equal to [math]\displaystyle{ 0 }[/math], so that we may solve for [math]\displaystyle{ t_\text{o} }[/math]:

[math]\displaystyle{ v_x(t_\text{o}) = 6.534t_\text{o} - \frac{{t_\text{o}}^4}{4} + \frac{{t_\text{o}}^3}{6} + 2565.93 = 0 }[/math]

Using a graphing calculator, we can solve the polynomial. The only solutions are [math]\displaystyle{ t_\text{o} = -9.84 \ \text{and} \ t_\text{o} = 10.30 }[/math]. We reason that only the second solution makes sense and that at [math]\displaystyle{ t_\text{o} = 10.30 }[/math] seconds the block comes to rest.

Technical Usage

Terminology

Let's imagine there is a right triangle. The side opposite to the right angle is a Slant. The side on the bottom is Run. The side vertical to the bottom is Rise.

Slope: A slope brings a mechanical advantage to the incline plane.

[math]\displaystyle{ \theta = \tan^{-1} \bigg( \frac {\text{Rise}}{\text{Run}} \bigg) \, }[/math]

Mechanical Advantage

[math]\displaystyle{ F_W }[/math] is a gravitational force that applies on the plane
[math]\displaystyle{ F_i }[/math] is a force exerted on the object and parallel to the plane
[math]\displaystyle{ \mathrm{MA} }[/math] is the Mechanical Advantage

[math]\displaystyle{ \mathrm{MA} = \frac{F_w}{F_i}. \, }[/math]

if the inclined plane is frictionless,

[math]\displaystyle{ \text{MA} = \frac{F_w}{F_i} = \frac {1}{\sin \theta} \, }[/math] (in this case, [math]\displaystyle{ \sin \theta = \frac {\text{Rise}}{\text{Length}} \, }[/math])

if the inclined plane has a friction

[math]\displaystyle{ \mathrm{MA} = \frac {F_w}{F_i} = \frac {\cos \phi} { \sin (\theta - \phi ) } \, }[/math] (in this case, [math]\displaystyle{ \phi = \tan^{-1} \mu \, }[/math])

[math]\displaystyle{ \theta \lt \phi\, }[/math]: Downhill applied force is needed.

[math]\displaystyle{ \theta = \phi\, }[/math]: Infinite mechanical advantage.

[math]\displaystyle{ \theta \gt \phi\, }[/math]: The mechanical advantage is positive. Uphill force is needed.

History

An inclined plane is one of the six classical simple machines defined by Renaissance scientists. They have been used for thousands of years to move large objects to a specific distance, such as with the potential creation of the Stonehenge or the formation of the Egyptian Pyramids. In the second century B.C., Archimedes began theorizing some of the properties associated with an inclined plane including its various applications. Then in the first century A.D., Hero of Alexandria went beyond Archimedes initial theories to further explain the functionality of an inclined plane. These theories then proved to be a reality as the years went on and there were more advancements and functions applied to inclined planes.

Connectedness

Every day people experience some sort of inclined plane. From driving up a hill on the way to work to walking down a ramp to get to class (because of all of the construction we always have), an inclined plane is a vital piece of our lives. What I find the most interesting about inclined planes is how people use them and physics for fun without even knowing it. Such as going down a slide at a park or skiing down a snowy mountain, the physics and forces behind an inclined plane bring enjoyment to many people's lives every day.

An inclined plane relates to mechanical engineering because MEs will always be working with various systems including some form of an inclined plane. Such as pulling an object across a ramp or the mechanics behind a water slide at an amusement park, inclined planes are everywhere. The best advice is to become comfortable with how they work and how to calculate the net force acting on the object sitting or moving on the inclined plane.

References

Cole, Matthew (2008). Explore science, 2nd Ed. Pearson Education. https://books.google.com/books?id=RhuciGEQ1G8C&pg=PA178#v=onepage&q&f=false

http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/incline.html

Inclined Plane

Contents

The Main Idea

A Mathematical Model

A Computational Model

Code

Examples

Simple

Middling

Difficult

Part I

Part II

Technical Usage

Terminology

Mechanical Advantage

History

Connectedness

See Also

References

Navigation menu