Electric Potential
Claimed by Gabriel Almeida Spring 2025
The Main Idea
Electric Potential Energy, like all forms of potential energy, is the potential for work to be done, in this case by the electric force. The Electric Potential (frequently referred to as voltage, from its SI unit, the Volt) is the Electric Potential Energy associated with the test charge (1 Coulomb), such that it depends only on the source, just as the electric field is related to the electric force, but depends only on the source. One may similarly remember the parallel concept of the gravitational potential, which was gravitational potential energy divided by mass.
A Mathematical Model
Electric Potential Energy is defined with respect to the Electric Force & Electric Field:
- [math]\displaystyle{ U_{ab} = - q \int_{b}^{a} \mathbf{E} \cdot d\mathbf{L} }[/math], where
- [math]\displaystyle{ U_{ab} }[/math] is the Electric Potential Energy from point b to point a
- [math]\displaystyle{ q }[/math] is the charge in the electric field
- [math]\displaystyle{ \mathbf{E} }[/math] is the source charge's electric field
- [math]\displaystyle{ d\mathbf{L} }[/math] is a differential length along the path from point b to point a
- [math]\displaystyle{ U_{ab} = - q \int_{b}^{a} \mathbf{E} \cdot d\mathbf{L} }[/math], where
The differential work [math]\displaystyle{ (dW) }[/math] associated with an external force [math]\displaystyle{ (\mathbf{F}_{ext}) }[/math] moving a charge [math]\displaystyle{ (q) }[/math] from point b to point a [math]\displaystyle{ (d\mathbf{L}) }[/math] through an electric field [math]\displaystyle{ (\mathbf{E}) }[/math] is:
- [math]\displaystyle{ dW = \mathbf{F}_{ext} \cdot d\mathbf{L} }[/math]
- This is the vector multiplication of the force moving the charge and the distance the object has moved.
The external force must be equal and opposite to the force associated with the source charge's electric field:
- [math]\displaystyle{ \begin{align} \mathbf{F}_{ext} &= - \mathbf{F}_{E} \\ &= - q \mathbf{E} \end{align} }[/math]
Therefore:
- [math]\displaystyle{ dW = - q \mathbf{E} \cdot d\mathbf{L} }[/math]
Integrating from point b to point a along the path gives:
- [math]\displaystyle{ W = -q \int_{b}^{a} \mathbf{E} \cdot d\mathbf{L} }[/math]
Finally, since the work was defined externally, the calculated work is equal to the Electric Potential Energy:
- [math]\displaystyle{ U_{ab} = -q \int_{b}^{a} \mathbf{E} \cdot d\mathbf{L} }[/math]
From this, the Electric Potential is defined as the Electric Potential Energy per test charge in the source charge's electric field:
- [math]\displaystyle{ V_{ab} = \frac{U_{ab}}{q} = - \int_{b}^{a} \mathbf{E} \cdot d\mathbf{L} }[/math]
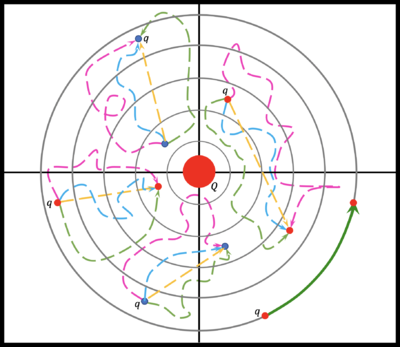
- The electric field is a conservative vector field:
- This means that any path used in the above line integral will give the same value for the same beginning and end points (b and a). Looking at the figure to the right, many paths for a charge [math]\displaystyle{ q }[/math] subject to the electric field of source charge [math]\displaystyle{ Q }[/math] are shown. In each set of four paths (Green, Blue, Yellow, and Pink), the same amount of Electric Potential Energy and Electric Potential is gained or lost.
- A special case shown in dark green near the bottom right of the figure also exists:
- If a charge is moving along a path that is always perpendicular to the electric field, the line integral will evaluate to zero, and therefore the Electric Potential Energy and Electric Potential will also evaluate to zero.
- This is easily shown with the dot product; if two variable vectors are always perpendicular, then their dot product is always zero.
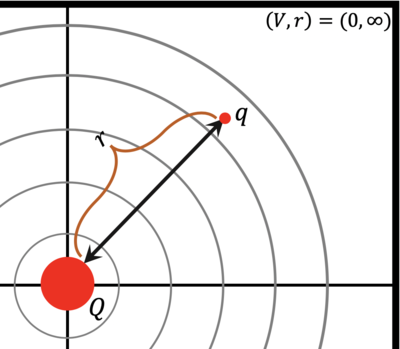
- The Electric Potential from a source charge [math]\displaystyle{ (Q) }[/math] can be written in a simpler expression:
- [math]\displaystyle{ V_{ab} = \frac{Q}{4 \pi \epsilon_{0}} \biggr ( \frac{1}{r_{a}} - \frac{1}{r_{b}} \biggr ) }[/math], where
- [math]\displaystyle{ Q }[/math] is the source charge
- [math]\displaystyle{ r_{a} }[/math] is the final position
- [math]\displaystyle{ r_{b} }[/math] is the initial position
- [math]\displaystyle{ V_{ab} = \frac{Q}{4 \pi \epsilon_{0}} \biggr ( \frac{1}{r_{a}} - \frac{1}{r_{b}} \biggr ) }[/math], where
- The initial position is often taken to be infinity (the Electric Potential is defined to be zero at infinity) creating a simpler and more familiar looking equation:
- [math]\displaystyle{ V_{ab} = \frac{Q}{4 \pi \epsilon_{0} r} }[/math], where
- [math]\displaystyle{ r }[/math] is the distance between the source charge and the charge in the electric field
- [math]\displaystyle{ V_{ab} = \frac{Q}{4 \pi \epsilon_{0} r} }[/math], where
- This is used to described the Electric Potential gained or lost when moving a charge radially closer to a source charge.
If a charge [math]\displaystyle{ (q) }[/math] is being moved in a source charge's [math]\displaystyle{ (Q) }[/math] electric field [math]\displaystyle{ (\mathbf{E}) }[/math] the Electric Potential Energy is:
- [math]\displaystyle{ U_{ab} = - q \int_{b}^{a} \mathbf{E} \cdot d\mathbf{L} }[/math]
The electric field is known to be described radially as: (Electric Field)
- [math]\displaystyle{ \mathbf{E} = \frac{1}{4 \pi \epsilon_{0}} \frac{Q}{r^2} \hat{\mathbf{r}} }[/math]
Allow the path be along the radial direction:
- [math]\displaystyle{ d\mathbf{L} = dr \hat{\mathbf{r}} }[/math]
Plugging these in gives:
- [math]\displaystyle{ \begin{align} U_{ab} &= -q \int_{b}^{a} \frac{1}{4 \pi \epsilon_{0}} \frac{Q}{r^2} \hat{\mathbf{r}} \cdot \hat{\mathbf{r}} dr \\ &= -q \int_{b}^{a} \frac{1}{4 \pi \epsilon_{0}} \frac{Q}{r^2} dr \\ &= - \frac{qQ}{4 \pi \epsilon_{0}} \int_{b}^{a} \frac{dr}{r^2} \\ &= \frac{qQ}{4 \pi \epsilon_{0}} \biggr [ \frac{1}{r} \biggr ]_{b}^{a} \\ &= \frac{qQ}{4 \pi \epsilon_{0}} \biggr ( \frac{1}{r_{a}} - \frac{1}{r_{b}} \biggr ) \\ \end{align} }[/math]
Therefore, the Electric Potential is:
- [math]\displaystyle{ V_{ab} = \frac{Q}{4 \pi \epsilon_{0}} \biggr ( \frac{1}{r_{a}} - \frac{1}{r_{b}} \biggr ) }[/math]
- Critical Formulas
- [math]\displaystyle{ U_{ab} = - q \int_{b}^{a} \mathbf{E} \cdot d\mathbf{L} }[/math]
- [math]\displaystyle{ V_{ab} = \frac{U_{ab}}{q} }[/math]
- [math]\displaystyle{ V_{ab} = \frac{Q}{4 \pi \epsilon_{0} r} }[/math]
A Computational Model
Click on the link to see Electric Potential through VPython! Make sure to press "Run" to see the principle in action!
Click the link below and press run to see a visual model of electric potential in space with equal and opposite charges (Press "Run")
Watch this video for a more visual approach!
Examples
Simple
A parallel plate capacitor is shown below:
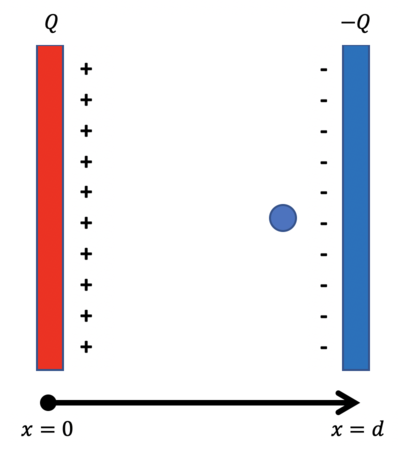
Each plate has area [math]\displaystyle{ A }[/math] with positive charge [math]\displaystyle{ Q }[/math] on the left plate and negative charge [math]\displaystyle{ -Q }[/math] on the right plate. The distance between the plates is [math]\displaystyle{ d }[/math].
- Question 1:
- a.) Which direction is the electric field between the plates pointed? How do you know?
Electric fields always point from positive to negative charge. Therefore, the electric field between the plates will point in the positive [math]\displaystyle{ x }[/math]-direction, straight from the left plate to the right plate since the distribution of positive and negative charge is flat and symmetric. The electric field will bend near the edges (called fringing fields). These are usually neglected if [math]\displaystyle{ d }[/math] is much smaller than the length of the plates.
- Question 2:
- b.) If the negative charge shown to be located near the negatively charged plate moved towards the positively charged plate, how would the electric potential and electric potential energy of the negative charge change?
We start with noting that the charge ([math]\displaystyle{ q_n=-\alpha q, \alpha \gt 0 }[/math]) in question is a negative charge. This effectively means all analysis will be reversed i.e. if the electric potential energy was increasing for a positive charge, it would be decreasing for a negative charge. With that said, we can start by noticing that the charge is moving against the electric field between the plates. Since this a negative charge, this is the way that negative charge wants to move, meaning it is losing electric potential energy and gaining kinetic energy. This can be seen mathematically by the following:
[math]\displaystyle{ U_{ab} = -q \int_b^a \mathbf{E} \cdot d \mathbf{L} = - (q_n) (-E_o) \Delta L = (-\alpha q)E_o \Delta L = -\alpha q E_o \Delta L }[/math] (since the electric field is approximately constant between the plates & the electric field and path are aligned)
We can readily see that moving from position [math]\displaystyle{ b }[/math] to position [math]\displaystyle{ a }[/math] (a distance of length [math]\displaystyle{ \Delta L }[/math]) causes a decrease in electric potential energy since this is a negative charge.
Now dividing [math]\displaystyle{ U_{ab} }[/math] by [math]\displaystyle{ q_n }[/math] gives [math]\displaystyle{ V_{ab} }[/math]:
[math]\displaystyle{ V_{ab} = \frac{U_{ab}}{q_n} = \frac{U_{ab}}{-\alpha q} = E_o \Delta L }[/math]
Therefore the electric potential is increasing.
- Question 3:
- c.) Redo part (b.) for a positive charge.
We can reverse our answer from b. but keep in mind electric potential is per unit test charge...essentially it is charge independent. Therefore, the electric potential energy of the positive charge would be increasing ([math]\displaystyle{ \alpha q E_o \Delta L }[/math]), and the electric potential would still be increasing.
Middling
A positive charge [math]\displaystyle{ q_o }[/math] travels through a spatially uniform electric field from Point [math]\displaystyle{ A }[/math] to Point [math]\displaystyle{ B }[/math] to Point [math]\displaystyle{ C }[/math], was depicted in the figure below. The coordinates of the points and magnitude of the electric field are defined in the figure.
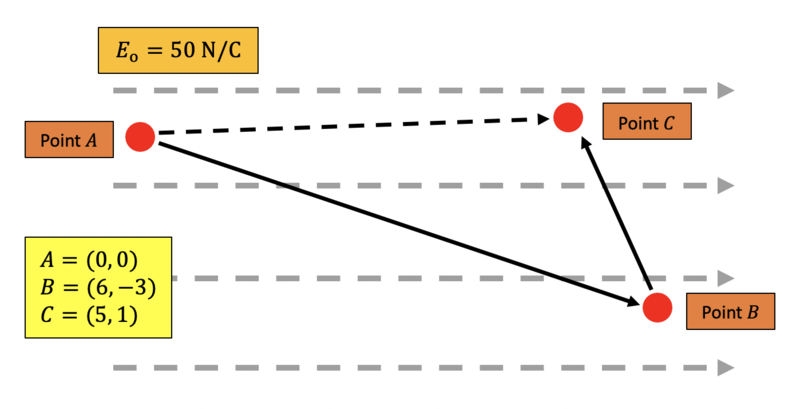
- Question 1:
- a.) When the charge moves from Point [math]\displaystyle{ A }[/math] to Point [math]\displaystyle{ B }[/math], what is the change in electric potential?
[math]\displaystyle{ V_{AB} = - \int_B^A \mathbf{E} \cdot d \mathbf{L} }[/math]
In this case, the electric field is a constant [math]\displaystyle{ (E_o, 0) }[/math], and the path is a straight line with components: [math]\displaystyle{ \Delta \mathbf{L} = A-B = (0, 0) - (6, -3) = (-6, 3) }[/math]
Our expression for the change in electric potential simplifies to: [math]\displaystyle{ V_{AB} = -\mathbf{E} \cdot \Delta \mathbf{L} = -(E_o, 0) \cdot (-6, +3) = 6E_o = 6E_o = 300 \ \mathrm{V} }[/math]
- Question 2:
- b.) When the charge moves from Point [math]\displaystyle{ B }[/math] to Point [math]\displaystyle{ C }[/math], what is the change in electric potential?
The process is exactly the same as part a: [math]\displaystyle{ V_{BC} = -\int_C^B \mathbf{E} \cdot \Delta \mathbf{L} = - (E_o, 0) \cdot (1, -4) = -E_o = -50 \ \mathrm{V} }[/math]
- Question 3:
- c.) If instead of moving from Point [math]\displaystyle{ A }[/math] to Point [math]\displaystyle{ B }[/math] to Point [math]\displaystyle{ C }[/math], the charge moved from Point [math]\displaystyle{ A }[/math] directly to Point [math]\displaystyle{ C }[/math], what would the change in electric potential be? How is this electric potential difference related to the two previously calculated electrical potential differences? What feature of an electric filed is this illustrating?
We repeat the same process again: [math]\displaystyle{ V_{AC} = -\int_C^A \mathbf{E} \cdot \Delta \mathbf{L} = - (E_o, 0) \cdot (-5, 1) = 5E_o = 250 \ \mathrm{V} }[/math]
The three calculated electric potential differences are related by: [math]\displaystyle{ V_{AC} = V_{AB} + V_{BC} = 250 \ \mathrm{V} }[/math]
This illustrates the path independence of the potential difference, and thus the conservative nature of the electric field.
Difficult
Problem:
Three identical point charges + 𝑞 are placed at the corners of an equilateral triangle of side length 𝑎 . A fourth point 𝑃 is located directly above the centroid of the triangle at a vertical height ℎ .
(a) Calculate the electric potential at point 𝑃 due to the three charges. Express your answer in terms of 𝑞 , 𝑎 , ℎ , and physical constants.
The electric potential due to a point charge is:
[math]\displaystyle{ V = \frac{1}{4\pi \varepsilon_0} \cdot \frac{q}{r} }[/math]
Since potential is a scalar, the total potential is just the sum of the contributions from each charge:
[math]\displaystyle{ V = \sum_{i=1}^{3} \frac{1}{4\pi \varepsilon_0} \cdot \frac{q}{r_i} }[/math]
Because point 𝑃 lies directly above the centroid, each distance 𝑟 𝑖
is the same.
We calculate this using the Pythagorean theorem:
The horizontal distance from any vertex to the centroid of an equilateral triangle is:
[math]\displaystyle{ r_{\text{base}} = \frac{a}{\sqrt{3}} }[/math]
Thus, the full distance from each charge to point 𝑃 P is:
[math]\displaystyle{ r = \sqrt{r_{\text{base}}^2 + h^2} = \sqrt{\frac{a^2}{3} + h^2} }[/math]
Plugging into the formula:
[math]\displaystyle{ V = 3 \cdot \frac{1}{4\pi \varepsilon_0} \cdot \frac{q}{\sqrt{ \frac{a^2}{3} + h^2 }} }[/math]
Final Answer
[math]\displaystyle{ \boxed{ V = \frac{3q}{4\pi \varepsilon_0 \sqrt{ \frac{a^2}{3} + h^2 }} } }[/math]
Connectedness
Electric potential is deeply woven into many branches of physics and engineering, often acting as a unifying concept for understanding energy, fields, and forces in electrical systems.
In electrostatics, potential provides an alternative to the electric field — rather than focusing on vector directions of force, potential simplifies analysis by using scalar values. This is especially powerful in systems with symmetry, where calculating potential is often much easier than finding the field directly.
In circuits, electric potential becomes the more familiar voltage, representing the energy per unit charge available to move charges through components. The entire theory of DC and AC circuit analysis relies on understanding potential differences across resistors, capacitors, and inductors.
In energy conservation, potential plays a key role. Just as gravitational potential energy helps us calculate the motion of falling objects, electric potential energy allows us to determine how charges move in electric fields. It’s one of the few concepts that links statics (equilibrium) and dynamics (motion) so seamlessly.
In quantum mechanics, electric potential enters the Schrödinger equation, shaping potential wells, barriers, and quantum tunneling behavior — core features in everything from semiconductors to atomic structure.
Even in materials science and chemistry, potential is central. Electrochemical potential drives redox reactions in batteries and electroplating, and molecular electrostatic potential maps help visualize where reactions will occur on a molecule. Therefore, it is extremely important to understand the fundamental of electric potential. It has many many uses.
History
The concept of electric potential has a long, illustrious history that dates back many centuries. Otto von Guericke, William Gilbert, and Robert Boyle were among the pioneering scientists who contributed to the study of electricity in the 17th century. The idea of electric potential did not start to take form until the 18th century, however.
French scientist Charles Du Fay discovered in 1733 that friction could charge certain materials, including amber, and that this charge could be transmitted to other things. Du Fay also observed that depending on the sign of their charges, two charged items might either attract or repel one another when placed near to one another.
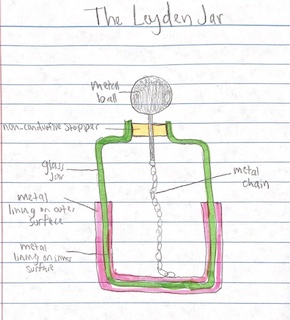
Both Dutch scientist Pieter van Musschenbroek and German physicist Ewald Georg von Kleist independently devised the Leyden jar, a device that could hold an electric charge, in 1745. The Leyden jar was simply a glass jar with a wire or rod put through the cork and either water or metal foil within. The charge would be kept in the jar until the wire was charged.
Charles-Augustin de Coulomb, a French scientist, first proposed the idea of electric potential energy in 1785. In an electric field, Coulomb demonstrated that the amount of labor needed to transfer a charged particle from one location to another was proportional to the difference in electric potential between the two sites. In the 19th century, Scottish scientist James Clerk Maxwell and German physicist Georg Simon Ohm expanded on this idea.
Electric potential is a key idea in physics today and is applied in a variety of domains, including electronics, electrical engineering, and the study of charged particle behavior in electromagnetic fields.
See also
Further Reading
David J. Griffiths – Introduction to Electrodynamics A widely respected textbook that introduces electric potential rigorously and clearly, with mathematical derivations and physical intuition. ISBN: 978-1108420419
Edward M. Purcell & David J. Morin – Electricity and Magnetism (Berkeley Physics Course, Vol. 2) Provides a more visual and conceptual explanation of electrostatics and potential, with real-world analogies and examples. ISBN: 978-1107014022
The Feynman Lectures on Physics, Volume II Chapters 4 and 5 walk through electric potential with Feynman's trademark intuition and analogies. Free to read online at feynmanlectures.caltech.edu
Paul Tipler & Gene Mosca – Physics for Scientists and Engineers A solid undergrad-level book with worked problems and clear visuals that connect potential to circuits and energy concepts. ISBN: 978-1429201247
MIT OpenCourseWare – 8.02 Electricity and Magnetism Free full lecture series, notes, and practice problems with strong coverage of electric potential and energy. https://ocw.mit.edu/courses/8-02sc-physics-ii-electricity-and-magnetism-fall-2010/
Khan Academy – Electric Potential Topics Intuitive videos and practice problems on potential, potential difference, and energy in electric fields. https://www.khanacademy.org/science/physics/electric-charge-electric-force
HyperPhysics – Electric Potential Quick-reference resource for equations, diagrams, and topic summaries. http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html
Matter & Interactions by Chabay and Sherwood A modern physics approach using computational modeling and treating potential as a central energy concept. ISBN: 978-1118875865
Externals links
References
Examples
Middling
Calculate the change in electric potential between point A, which is at [math]\displaystyle{ (-4, 3,0) \; m }[/math], and B, which is at [math]\displaystyle{ (2,-2,0) \; m }[/math] . The electric field in the location is [math]\displaystyle{ (50,0,0) \; N/C }[/math].
Answer: -300V
Explanation:
[math]\displaystyle{ \Delta\vec{l}= (2,-2,0)\;m - (-4,3,0)\;m = (6,-5,0)\;m }[/math]
[math]\displaystyle{ \Delta{V} = -({E}_{x}∆{x} + {E}_{y}∆{y} + {E}_{z}∆{z}) }[/math]
[math]\displaystyle{ \Delta{V} = -(50\; N/C \cdot 6 \;m + 0 \; N/c \cdot -5 \; m + 0\cdot 0) }[/math]
[math]\displaystyle{ \Delta{V} = -300 V }[/math]
Difficult
The Bohr Model of the hydrogen atom treats it as a nucleus of charge [math]\displaystyle{ +e }[/math] electrons of charge [math]\displaystyle{ -e }[/math] orbiting in circular orbits of specific radii. Calculate the potential difference between two points, one infinitely far away from the nucleus, and the other one Bohr radius [math]\displaystyle{ a_0 }[/math] away from the nucleus (don't worry about substituting in the values). Compute the electric potential energy associated with the electron one Bohr radius away from the nucleus, setting the potential energy at infinity as zero (remember the sign of the charge).
We may compute the electric potential by taking integrating the electric field of a point charge as the radius goes from infinity to [math]\displaystyle{ a_0 }[/math]. This integral may be set up as:
[math]\displaystyle{ \Delta V = -\int_\infty^{a_0} \vec{E}\cdot\text{d}\vec{l} }[/math]
[math]\displaystyle{ \Delta V = -\frac{e}{4\pi\epsilon_0} \int_\infty^{a_0} \frac{\text{d} r}{r^2} }[/math]
This may then be solved:
[math]\displaystyle{ \Delta V = \frac{e}{4\pi\epsilon_0}\biggr{(}\frac{1}{r}\biggr{|}_\infty^{a_0} = \frac{e}{4\pi\epsilon_0 a_0} }[/math]
to compute the potential energy, we now multiply by the charge of the electron: [math]\displaystyle{ -e }[/math], giving
[math]\displaystyle{ U = -\frac{e^2}{4\pi\epsilon_0 a_0} }[/math]
Depending on what physics or chemistry courses you may have taken before, this may be recognizable as twice the ionization energy of the n=1 orbital. The factor of two is due to the fact that in the Bohr model, the kinetic energy will be exactly half of this potential energy, and will be positive so that the net result is still negative, but with half the magnitude. This understanding of the hydrogen atom gets certain values right, but the reality of the situation is far more complicated.
Connectedness
How is this topic connected to something that you are interested in?
[Author] I am interested in robotic systems and building circuit boards and electrical systems for manufacturing robots. While studying this section in the book, I was able to connect back many of the concepts and calculations back to robotics and the electrical component of automated systems.
[Revisionist] Since high school, I never really understood how to work with the voltmeter and what it measured, and I have always wanted to know, but although this particular wiki page did not go into the details and other branches of electric potential, it led me to find the answers to something I was interested in since high school, the concept of electric potential.
[Editor] I think electively is really interesting. When I was younger, I participated in this demo where a group of people hold hands and someone touches this special ball full of charge. We all could feel the tingling sensation of the current passing through us. It’s cool to learn the theory behind the supposed magic that occurs.
[FALL 2018] I think it's very interesting that electric potential can be seen as a property of a space and that we can have further applications using this property.
How is it connected to your major?
[Author] I am a Mechanical Engineering major, so I will be dealing with the electrical components of machines when I work. Therefore, I have to know these certain concepts such as electric potential in order to fully understand how they work and interact.
[Revistionist] As a biochemistry major, electric potential and electric potential difference is not particularly related to my major, but in chemistry classes, we use electrostatic potential maps (electrostatic potential energy maps) that shows the charge distributions throughout a molecule. Although the main use in electric potential is different in physics and biochemistry (where physicists use it identify the effect of the electric field at a location), I still found it interesting as the concept of electric potential (buildup) was being used in quite a different way.
[Editor] I am a computer science major. Although I deal mostly with software, the hardware aspect is still important. The algorithms that I design run differently on different machines. The time complexity of an algorithm is sometimes useless when worrying about constant factors that are determined by a system’s hardware. Quicksort, for instance, is usually faster than many other sorts that have lower time complexities. The hardware of computers heavily relies on electricity and current (which is induced by a potential difference) to switch transistors on and off and thereby process information.
[FALL 2018] I am an aerospace engineering major, and I think understanding such concepts will help me have a better holistic understanding towards fields and systems. In addition, the thinking behind solving related problems will help me better prepared for future classes that involve with solving dynamics problems.
Is there an interesting industrial application?
[Author] Electrical potential is used to find the voltage across a path. This is useful when working with circuit components and attempting to manipulate the power output or current throughout a component.
[Revisionist] Electric potential sensors are being used to detect a variety of electrical signals made by the human body, thus contributing to the field of electrophysiology.
[Editor] The study of electric potential has lead scientists to generate very safe wires that will not overheat and cause fires. Connecting circuits to ground is important and the third prong in an electrical outlet is this ground connection.
History
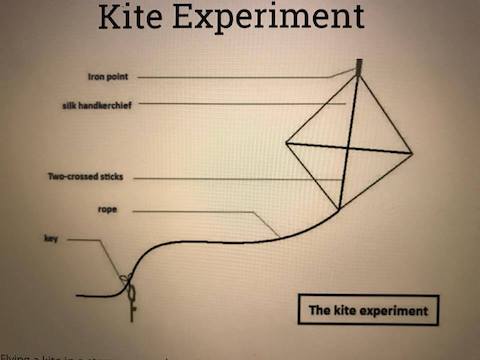
The idea of electric potential, in a way, started with Ben Franklin and his experiments in the 1740s. He began to understand the flow of electricity, which eventually paved the path towards explaining electric potential and potential difference. Scientists finally began to understand how electric fields were actually affecting the charges and the surrounding environment. Benjamin Franklin first shocked himself in 1746, while conducting experiments on electricity with found objects from around his house. Six years later, or 261 years ago for us, the founding father flew a kite attached to a key and a silk ribbon in a thunderstorm and effectively trapped lightning in a jar. The experiment is now seen as a watershed moment in mankind's venture to channel a force of nature that was viewed quite abstractly.
By the time Franklin started experimenting with electricity, he'd already found fame and fortune as the author of Poor Richard's Almanack. Electricity wasn't a very well understood phenomenon at that point, so Franklin's research proved to be fairly foundational. The early experiments, experts believe, were inspired by other scientists' work and the shortcomings therein.
source: http://www.benjamin-franklin-history.org/kite-experiment/
That early brush with the dangers of electricity left an impression on Franklin. He described the sensation as "a universal blow throughout my whole body from head to foot, which seemed within as well as without; after which the first thing I took notice of was a violent quick shaking of my body." However, it didn't scare him away. In the handful of years before his famous kite experiment, Franklin contributed everything from designing the first battery designs to establishing some common nomenclature in the study of electricity. Although Franklin is often coined the father of electricity, after he set the foundations of electricity, many other scientists contributed his or her research in the advancement of electricity and eventually led to the discovery of electric potential and potential difference.
See also
Like mentioned multiple times throughout the page, although electric potential is a huge and important topic, it has many branches, which makes the concept of electric potential difficult to stand alone. Even with this page, to support the concept of electric potential, many crucial branches of the topic appeared, like potential difference (which also branched into [Potential Difference Path Independence], [Potential Difference In A Uniform Field], and [Potential Difference In A Nonuniform Field]).
External Links
[2] https://www.youtube.com/watch?v=pcWz4tP_zUw
[3] https://www.youtube.com/watch?v=Vpa_uApmNoo
References
[1] "Benjamin Franklin and Electricity." Benjamin Franklin and Electricity. N.p., n.d. Web. 17 Apr. 2016. <http://www.americaslibrary.gov/aa/franklinb/aa_franklinb_electric_1.html>.
[2] Bottyan, Thomas. "Electrostatic Potential Maps." Chemwiki. N.p., 02 Oct. 2013. Web. 17 Apr. 2016. <http://chemwiki.ucdavis.edu/Core/Theoretical_Chemistry/Chemical_Bonding/General_Principles_of_Chemical_Bonding/Electrostatic_Potential_maps>.
[3] "Electric Potential Difference." Electric Potential Difference. The Physics Classroom, n.d. Web. 14 Apr. 2016. <http://www.physicsclassroom.com/class/circuits/Lesson-1/Electric-Potential-Difference>.
[4] Harland, C. J., T. D. Clark, and R. J. Prance. "Applications of Electric Potential (Displacement Current) Sensors in Human Body Electrophysiology." International Society for Industrial Process Tomography, n.d. Web. 16 Apr. 2016. <http://www.isipt.org/world-congress/3/269.html>.
[5] Sherwood, Bruce A. "2.1 The Momentum Principle." Matter & Interactions. By Ruth W. Chabay. 4th ed. Vol. 1. N.p.: John Wiley & Sons, 2015. 45-50. Print. Modern Mechanics.