Potential Difference Path Independence, claimed by Aditya Mohile
Claimed by Emaan Jalal (Spring 2025)
Claimed by Aditya Mohile (Spring 2016)
Claimed by Zachary Wright (Fall 2016)
Potential Difference and Path Independence
Potential difference, also known as voltage, is a scalar quantity that represents the difference in electric potential energy per unit charge between two points in an electric field. This difference depends only on the initial and final states of the system, not on the specific path taken to move between these two points. As a result, potential difference is said to be path independent.
The path independence of potential difference arises because electric fields in electrostatics are conservative fields. In such fields, the work done to move a charge between two points depends solely on the starting and ending positions, not on the trajectory. This fundamental property simplifies calculations in physics and engineering.
The unit of measurement for potential difference is joules per coulomb (J/C), which is equivalent to volts (V).
The Main Idea
The key concept behind path independence is that the potential difference between two points remains constant regardless of the route taken to travel between them. This is because potential difference is determined solely by the relative positions of the two points within the electric field, not by how the charge moves from one point to another.
A Mathematical Model
- [math]\displaystyle{ \Delta V_{AB} = \int_{A}^{B} \vec{E} \cdot d\vec{l} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
The potential difference, [math]\displaystyle{ \Delta V_{AB} }[/math], is the integral of the electrical field from point A to point B. This integral, however, is the dot product of [math]\displaystyle{ \vec{E} }[/math] and [math]\displaystyle{ d\vec{l} }[/math] which is equal to the sum of the negative electric field multiplied by the difference of the x,y and z components of the two points, as see from the equation above. This proves that the path taken from point A to point B does not matter, only the difference in the positions of points A and B are important in calculating the potential difference.
As shown above, the potential difference between points A and B in the electric field E is independent of the path.
A Computational Model
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple

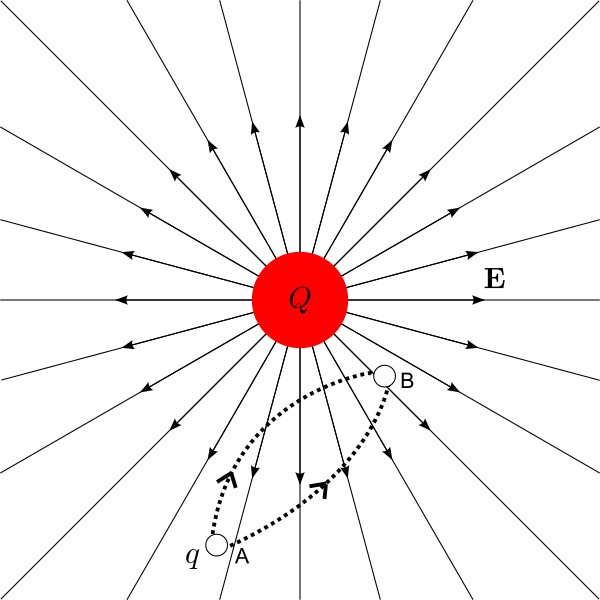
Problem: Locations A, B, and C are in a region of uniform electric field, as shown in the diagram above. Location A is at < -0.6, 0, 0> m. Location B is at < 0.4, 0, 0>. Location C is at < 0.4, -0.3, 0>m. In the region the electric field = < -750, 400, 0> N/C. Calculate the potential difference between A and C traveling from A to B then to C. Calculate the potential difference traveling from A to C directly.
Step 1
- Calculate the displacement vector from A to B.
- [math]\displaystyle{ \Delta l = \lt 0.4, 0, 0\gt - \lt -0.6, 0, 0\gt = \lt 1, 0, 0\gt }[/math]
Step 2
- Calculate the potential difference between A and B.
- [math]\displaystyle{ \Delta V_{AB} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AB} = -(-750*1 + 400*0 + 0*0) = 750V }[/math]
Step 3
- Calculate the displacement vector from B to C.
- [math]\displaystyle{ \Delta l = \lt 0.4, -0.3, 0\gt - \lt 0.4, 0, 0\gt = \lt 0, -0.3, 0\gt }[/math]
Step 4
- Calculate the potential difference between B and C.
- [math]\displaystyle{ \Delta V_{BC} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{BC} = -(-750*0 + 400*-0.3 + 0*0) = 120V }[/math]
Step 5
- Add [math]\displaystyle{ \Delta V_{AB} }[/math] to [math]\displaystyle{ \Delta V_{BC} }[/math] to get [math]\displaystyle{ \Delta V_{AC} }[/math]
- [math]\displaystyle{ \Delta V_{AC} = \Delta V_{AB} + \Delta V_{BC} = 750 + 120 = 870V }[/math]
Now you have to calculate the potential difference from A to C directly.
Step 1
- Calculate the displacement vector from A to C.
- [math]\displaystyle{ \Delta l = \lt 0.4, -0.3, 0\gt - \lt -0.6, 0, 0\gt = \lt 1, -0.3, 0\gt }[/math]
Step 2
- Calculate the potential difference between A and C.
- [math]\displaystyle{ \Delta V_{AB} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AB} = -(-750*1 + 400*-0.3 + 0*0) = 750 + 120 = 870V }[/math]
As you can see, potential difference from A to C directly is the same as the potential difference from A to B then to C.
Middling
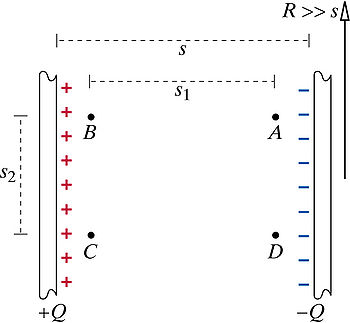
Problem: A capacitor consists of two charged disks of radius 4.7 m separated by a distance s = 2 mm (see the figure). The magnitude of the charge on each disk is 56 µC. Consider points A, B, C, and D inside the capacitor, as shown in the diagram. The distance s1 = 1.5 mm, and the distance s2 = 0.6 mm. (Assume the +x axis is to the right, the +y axis is up, and the +z axis is out.) Find the potential difference between B and D, traveling through A. Find the potential difference from B to D directly. Step 1
- Calculate the electric field inside the capacitor.
- [math]\displaystyle{ \vec E_{cap} = \frac{Q/A}{\epsilon_{0}} }[/math]
- [math]\displaystyle{ \vec E_{cap} = \frac{(56*10^{-6})/(\pi*4.7^{2})}{8.85*10^{-12}} = \lt 91179.912, 0, 0\gt }[/math]
The electric field only has an x-component because the field travels from the positively charged plate to the negatively charged plate, traveling in the +x direction.
Step 2
- Calculate the displacement vector from B to A.
- Set the origin at B.
- [math]\displaystyle{ \Delta l = \lt s_{1}, 0, 0\gt - \lt 0, 0, 0\gt = \lt s_{1}, 0, 0\gt = \lt 0.0015, 0, 0\gt }[/math]
Step 3
- Calculate the potential difference between B and A.
- [math]\displaystyle{ \Delta V_{BA} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{BA} = -(91179.912*0.0015 + 0*0 + 0*0) = -136.770V }[/math]
Step 4
- Calculate the displacement vector from A to D
- [math]\displaystyle{ \Delta l = \lt s_{1}, s_{2}, 0\gt - \lt s_{1}, 0, 0\gt = \lt 0, s_{2}, 0\gt = \lt 0, s_{2}, 0\gt = \lt 0, 0.006, 0\gt }[/math]
Step 5
- Calculate the potential difference between A and D.
- [math]\displaystyle{ \Delta V_{AD} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AD} = -(91179.912*0 + 0*0 + 0*0) = 0V }[/math]
Step 6
- Add [math]\displaystyle{ \Delta V_{BA} }[/math] to [math]\displaystyle{ \Delta V_{AD} }[/math] to get [math]\displaystyle{ \Delta V_{BD} }[/math]
- [math]\displaystyle{ \Delta V_{BD} = \Delta V_{BA} + \Delta V_{AD} = -136.770 + 0 = -136.770V }[/math]
Notice that the voltage is negative since we are going from the positively charged plate (high potential) to the negatively charged plate (low potential) losing potential energy in the process.
Now you have to calculate the potential difference from A to C directly.
Step 1
- Calculate the displacement vector from B to D.
- [math]\displaystyle{ \Delta l = \lt s_{1}, s_{2}, 0\gt - \lt 0, 0, 0\gt = \lt s_{1}, s_{2}, 0\gt = \lt s_{1}, s_{2}, 0\gt = \lt 0.0015, 0.006, 0\gt }[/math]
Step 2
- Calculate the potential difference between B and D.
- [math]\displaystyle{ \Delta V_{AD} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AD} = -(91179.912*0.0015 + 0*0 + 0*0) = -136.770V }[/math]
Notice that potential difference traveling from B to A then D is the same as the potential difference traveling from B to D directly. This exemplifies that the potential difference does not depend on the path taken to get from one point to another.
Difficult

Problem: A uniform spherical shell of charge +Q is centered at point B, as shown in the figure below. Show that ΔV = VC − VA is independent of path by calculating ΔV for each of these two paths (actually do the integrals). (Use the following as necessary: Q, R for the radius of the spherical shell, r1 for the radius of the circular arc A → D → C with B at its center, and ε0.)
Step 1
- Calculate the potential difference from A to C following the path A → B → C.
- First, calculate the potential difference from A to B.
- [math]\displaystyle{ \Delta V_{AB} = \int_{A}^{B} \vec{E} \cdot d\vec{l} }[/math]
- In order to calculate the potential difference from A to B, calculate the electric field of the sphere.
- [math]\displaystyle{ \vec{E}_{sphere} = \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} }[/math]
- Now plug the electric field calculated above into the integral and solve.
- [math]\displaystyle{ \Delta V_{AB} = \int_{A}^{B} \vec{E} \cdot d\vec{r} = \int_{r_{1}}^{R} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{R^{2}} - \frac{Q}{r_{1}^{2}}) }[/math]
- Now calculate the potential difference from B to C.
- Use the electric field of the sphere calculated above to solve the below integral.
- [math]\displaystyle{ \Delta V_{BC} = \int_{B}^{C} \vec{E} \cdot d\vec{l} }[/math]
- [math]\displaystyle{ \Delta V_{BC} = \int_{R}^{r_{1}} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{R^{2}}) }[/math]
- Now add [math]\displaystyle{ \Delta V_{AB} }[/math] to [math]\displaystyle{ \Delta V_{BC} }[/math] to get [math]\displaystyle{ \Delta V_{AC} }[/math]
- [math]\displaystyle{ \Delta V_{AC} = \Delta V_{AB} + \Delta V_{BC} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{R^{2}} - \frac{Q}{r_{1}^{2}}) + \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{R^{2}}) = 0V }[/math]
Step 2
- Calculate the potential difference from A to C following the path A → D → C.
- First calculate the potential difference from A to D.
- [math]\displaystyle{ \Delta V_{AD} = \int_{A}^{D} \vec{E} \cdot d\vec{l} }[/math]
- Use the same electric field of the sphere calculated in step 1, shown below.
- [math]\displaystyle{ \vec{E}_{sphere} = \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} }[/math]
- Now plug the electric field calculated above into the integral and solve.
- [math]\displaystyle{ \Delta V_{AD} = \int_{A}^{D} \vec{E} \cdot d\vec{r} = \int_{r_{1}}^{r_{1}} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) = 0V }[/math]
- Now calculate the potential difference from D to C.
- Use the electric field of the sphere calculated above to solve the below integral.
- [math]\displaystyle{ \Delta V_{DC} = \int_{D}^{C} \vec{E} \cdot d\vec{l} }[/math]
- [math]\displaystyle{ \Delta V_{DC} = \int_{r_{1}}^{r_{1}} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) }[/math]
- Now add [math]\displaystyle{ \Delta V_{AD} }[/math] to [math]\displaystyle{ \Delta V_{DC} }[/math] to get [math]\displaystyle{ \Delta V_{AC} }[/math]
- [math]\displaystyle{ \Delta V_{AC} = \Delta V_{AD} + \Delta V_{DC} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) + \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) = 0V }[/math]
- Notice that either path taken from A to C results in the same potential difference of 0V.
Connectedness
How is this topic connected to something that you are interested in?
- I am very interested in electronics and circuitry so knowing that potential difference is path independent definitely helps in determining the voltage between 2 points in a complicated circuit with many paths.
How is it connected to your major?
- I am an electrical engineering major so this knowledge is very applicable to determining the voltage between 2 points in a circuit that contains many loops or is very complex.
Applications
- Power Distribution Systems: Engineers use this principle to calculate voltage drops across transmission lines and ensure consistent power delivery to homes and businesses.
- Circuit Design: In industries like consumer electronics or automotive engineering, path independence helps optimize circuit layouts for devices like smartphones, electric vehicles, and medical equipment.
- Renewable Energy Systems: In solar panel arrays or wind turbine systems, path independence aids in designing efficient electrical networks that maximize energy transfer while minimizing losses.
- By leveraging this concept, industries can create reliable and efficient systems that meet modern technological demands.
History
Path independence of potential difference is fundamentally rooted in the Law of Conservation of Energy, a principle that evolved through centuries of scientific investigation. This concept traces back to early theoretical work in mechanics and later developed through experiments with electricity.
In 1687, Isaac Newton published his groundbreaking Principia Mathematica, which established the laws of motion and developed concepts of force and momentum that would later become crucial to understanding energy conservation. Although Newton's work did not directly address electrical potential, his mechanical framework laid the essential groundwork for future developments.
During the late 17th and early 18th centuries, Gottfried Wilhelm Leibniz championed the concept of vis viva (living force), which we now recognize as a form of kinetic energy. By the 1690s, Leibniz argued that the conservation of vis viva and momentum were fundamental principles governing physical interactions. This theoretical foundation was crucial for the later understanding of conservative fields, including electric fields, where path independence applies.
The mathematical exploration of energy conservation continued with father and son Johann Bernoulli and Daniel Bernoulli, who further developed Leibniz's ideas. Daniel Bernoulli's work on the kinetic theory of gases and hydrodynamics (published in 1738) anticipated formal laws of energy conservation. His investigations into energy transformations and efficiency helped establish the conceptual framework necessary for understanding potential energy in various systems.
Émilie du Châtelet made significant contributions by proposing and testing the conservation of total energy as distinct from momentum. Her experiments, inspired by Leibniz's theories, demonstrated that energy must maintain the same dimensions in any form—a critical insight for understanding potential difference.
The empirical validation of energy conservation came through James Prescott Joule's meticulous experiments in the 1840s. Joule's work established the mechanical equivalent of heat and helped formalize the first law of thermodynamics, confirming that energy can be converted between different forms but cannot be created or destroyed—a principle that explains why potential difference is path independent.
The concept of potential difference emerged more clearly through pioneering work in electricity during the late 18th and early 19th centuries. A pivotal moment came through the famous dispute between two Italian scientists.
In 1771, Luigi Galvani, an Italian physician and physicist, made a chance observation that would revolutionize electrical science. While dissecting a frog, he noticed that its leg muscles contracted when touched with a metal scalpel during a lightning storm. Through further experiments, Galvani discovered what he called "animal electricity"—observing that when two different metals connected in series touched a frog's leg, it would twitch. He concluded that the electricity originated within the animal tissues themselves.
Alessandro Volta (1745-1827), another Italian physicist, was initially intrigued by Galvani's work but developed a different interpretation. Volta suspected that the electricity was not generated by the animal tissue but resulted from the contact between different metals, with the frog leg merely serving as a conductor and detector of electricity (an electrolyte). To test this hypothesis, Volta replaced the frog leg with paper soaked in brine and observed similar results.
Volta's investigations led to his groundbreaking invention of the voltaic pile in 1800—the world's first battery capable of producing continuous electrical current. This device consisted of alternating disks of zinc and silver (or copper and pewter) separated by paper or cloth soaked in salt water or sodium hydroxide. The invention provided the first reliable source of continuous electrical current and initiated a wave of new electrical experiments.
Within weeks of Volta's announcement, William Nicholson and Anthony Carlisle used a voltaic pile to decompose water into hydrogen and oxygen, discovering electrolysis and establishing the field of electrochemistry. These developments were crucial in understanding how electrical potential energy could be converted to other forms—a key aspect of potential difference path independence.
The unit of electrical potential difference, the volt, was named in Volta's honor in 1881, recognizing his foundational contributions to electrical science.
Electromagnetic induction, another important phenomenon related to potential difference, was discovered by Michael Faraday in 1831 and independently by Joseph Henry in 1832. Faraday's concept of "lines of force" helped explain electromagnetic phenomena, though it wasn't until James Clerk Maxwell provided mathematical formulation of these ideas that the modern understanding of electromagnetic fields and potential was established.
The principle of path independence in potential difference ultimately emerges from the conservative nature of electrostatic fields—a direct consequence of energy conservation, which was established through centuries of theoretical and experimental work by these pioneering scientists.
See also
https://en.wikipedia.org/wiki/Voltage
Further reading
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elewor.html#c2
External links
References
Matter & Interactions volume II by Ruth W. Chabay and Bruce A. Sherwood.