Bohr Model

Introduction

This page gives basic information about the Bohr model of the atom and the quantization of electron angular momentum. These concepts are the basis of modern quantum physics and thus are essential to master before progressing to more complex quantum theories and principles. Although the Bohr model is regarded as inaccurate and outdated, the model predicts the hydrogen atom well and provides good predictions on quantized energy levels.

The Bohr Model was proposed in 1913 by the physicist Niels Bohr and is a description of the structure of atoms in which there is a dense positive core surrounded by orbiting electrons. In this model, the electrons orbit the nucleus in circular orbits, accounting for the series of discrete wavelengths in the H2 emission spectrum. Bohr's model of the hydrogen atom was the first to incorporate quantum theory, and the key idea of his model was that electrons occupy discrete orbitals.

Main Idea

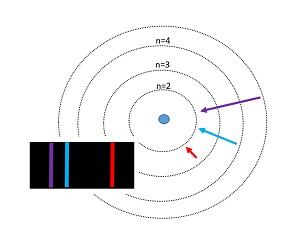
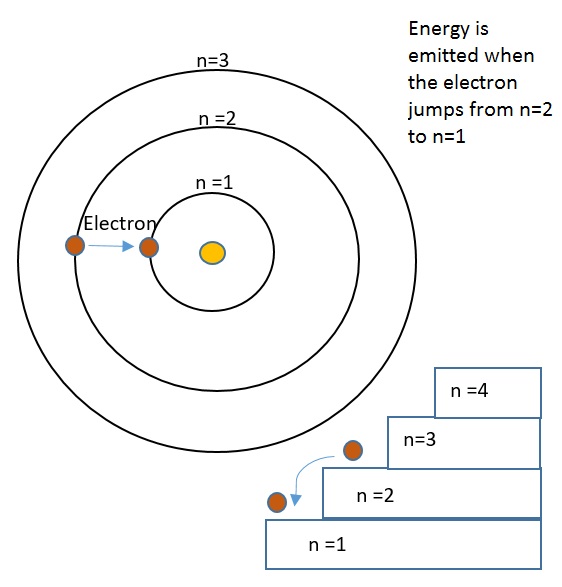
A visualization of the Bohr model and the hydrogen spectrum

The Bohr model of the atom was proposed by Niels Bohr in 1913 as an expansion on and correction of the Rutherford model. His model depicted atoms as having negatively charged electrons which orbited a small, positively charged nuclei containing most of the atom's mass, as Rutherford had done. However, the Bohr Model's incorporation of quantum theory set it apart from other models. In this model, electrons can only exist in discrete energy levels, which are quantized. The electrons orbit the nucleus at energy levels increasing (n= 1,2,3 ..) with their distance from the nucleus. Similar to stepping up a staircase, these energy levels are quantized. This model is very simplistic and is useful in introducing students to quantum mechanics. It also provides a decent first-order approximation of more complicated theories. Although this model successfully predicts energy levels of the hydrogen atom, it has major shortcomings once expanded to other atoms and more complex real-world situations. For example, one of the weaknesses of his analysis was not offering a reason for why only certain energy levels or orbitals were allowed.

Bohr's Assumptions

Electrons travel in a circular orbit around the nucleus, similar to how planets orbit around the sun. (This was Bohr's inspiration for the model, electrons orbiting the nucleus.) Holding these electrons in these orbits are electrostatic forces rather than gravity.
The energy of orbiting electrons is negative, in order to free an electron from the atom's orbit you must bring its energy to 0.
The energy of electrons is inversely related to their distance from the nucleus and which energy level they occupy at that distance. The further away from the electron, the more energy it has. (Electric Potential Energy) [math]\displaystyle{ U = ((k)q_{1}q_{2})/d }[/math] (With the k constant representing the electrostatic/Coulomb constant)
When electrons gain or lose energy they jump from one orbit to another. The energy is quantized - the orbitals have discreet radii or exact distances from the nucleus where electrons are allowed to exist, which Bohr called "stationary orbits."
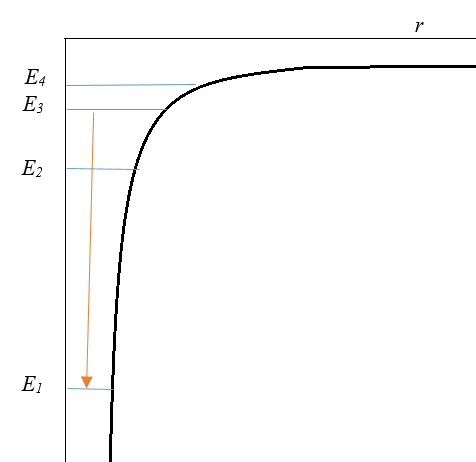
When an excited electron returns back to its ground state, then it releases the energy that is absorbed, in the form of a photon. All photons are produced by an electron transitioning to a lower energy level, or smaller radius or becoming closer to the nucleus. Conversely, an input of energy is required to transition an electron to a higher energy level. This quantized energy - in both cases - is equal to the difference between the respective energies of the orbits.

Stairs are a great way to visualize quantized energy. When you're going upstairs, you can only be standing on the steps, and not anywhere in between the steps. Similarly, energy can only be absorbed or emitted in specific quanta. Energy is required to go up the stairs, and energy is gained when jumping down from one stair to the next (in the electron's case, this energy is released as a photon - sometimes as visible light!).

Application

A Mathematical Model

The Angular Momentum Quantum

[math]\displaystyle{ ħ = h/2π =1.05*10^{-34} J*s }[/math]

h is known as Planck's constant, which is a physical constant that is essential in quantum mechanical calculations.

Angular Momentum Is Quantized

Bohr assumed that electrons in orbit are only allowed very specific values for the magnitude of their angular momentum, specifically integer multiples of ħ given by:

[math]\displaystyle{ |\vec L_{trans,C}| = rp = Nħ }[/math]

L is the angular momentum of the electron, p is the Linear Momentum of the electron, r is the radius of the electron's orbit, and N is an integer (1,2,3, ...).

We can derive the equation for r, the allowed Bohr radii for electron orbits for hydrogen, which has one electron and one proton.

1) The Electric Force the proton exerts on the electron is calculated using: [math]\displaystyle{ F_{el} = {\frac{e^2}{4π ε_{0} r^2}} }[/math]

2) Applying concepts from the momentum principle and curving motion: [math]\displaystyle{ |F_{perpendicular}| = {\frac{|p| |v|}{r}} = {\frac{e^2}{4π ε_{0} r^2}} }[/math]

3) Substituting for the relation between momentum and velocity ([math]\displaystyle{ v = {\frac{p} {m_{e}}} }[/math]) where [math]\displaystyle{ m_{e} }[/math] is the mass of an electron: [math]\displaystyle{ {\frac{|p|}{r}} *{\frac{|p|}{m_{e}}} = {\frac{e^2}{4π ε_{0} r^2}} }[/math]

4) Substituting in Bohr's conditions for the magnitude of [math]\displaystyle{ p }[/math]: [math]\displaystyle{ {\frac{N^2 ħ^2}{m_{e}r^3}} = {\frac{e^2}{4π ε_{0} r^2}} }[/math]

5) Solving for the allowed radii [math]\displaystyle{ r = {\frac{4π ε_{0} ħ^2N^2}{m_{e}e^2}} }[/math] where N = 1,2,3,...

6) This result is often simplified to [math]\displaystyle{ r_{n} = a_{0}n^2 }[/math] where [math]\displaystyle{ a_{0} = {\frac{4π ε_{0}ħ^2}{m_{e}e^2}} = 0.0529 }[/math] nm and n = 1,2,3,...

Additionally, the formula for energy of hydrogen atom of different levels is also derived from this model, and is the formula most helpful for simple calculations involving quantum mechanics.

[math]\displaystyle{ E = K + U_{electromagnetic} }[/math]

1) [math]\displaystyle{ E = {\frac{mv^2}{2}} - {\frac{{\frac{1}{2}}*{\frac{1}{4π ε0}}*{\frac{me^2}{ħ}}}{N^2}} }[/math]

which simplifies to

2) [math]\displaystyle{ E = {\frac{13.6 eV}{N^2}} }[/math] where N = 1,2,3

Wavelengths

In the early 1900's, light had been observed to have the properties of both a particle and a wave. In 1924, Louis de Broglie, a French physicist, hypothesized all matter holds properties of waves in his thesis Recherches sur la théorie des quanta (Research on the Theory of the Quanta). According to de Broglie, there is an inverse relationship between momentum and wavelength.

The de Broglie relationship can tell us about the wavelength associated with the electron and can tell us the energy that will be released in photons, or particles of energy: [math]\displaystyle{ λ = \frac{h}{mv} }[/math] or [math]\displaystyle{ λ = \frac{h}{p} }[/math]

h is Planck's constant (6.63x10e-34 joules.sec), and v is the frequency or the velocity of the disturbance in the medium of propagation.

This equation is used to help derive the equation for the angular momentum of an electron in orbit [math]\displaystyle{ L = \frac{nh}{2π} }[/math]

Derivation of de Broglie's relationship:

E = energy, m = mass, c = speed of light,

Assuming that the two energies would be equal or in practical units:

1) [math]\displaystyle{ mc^2 = hv }[/math]

Since particles do not necessarily travel with the speed of light,

2) [math]\displaystyle{ mv^2 = hv = mv^2 = \frac{hv}{λ} }[/math] (using [math]\displaystyle{ hv = \frac{hc}{λ} }[/math])

Finally

3) [math]\displaystyle{ λ = \frac{hv}{mv^2} = \frac{h}{mv} }[/math]

A Computational Model

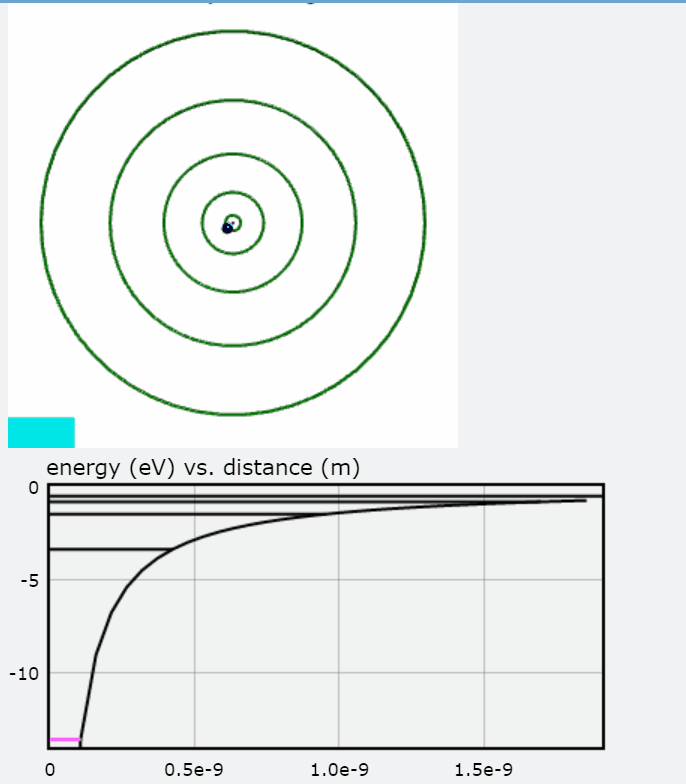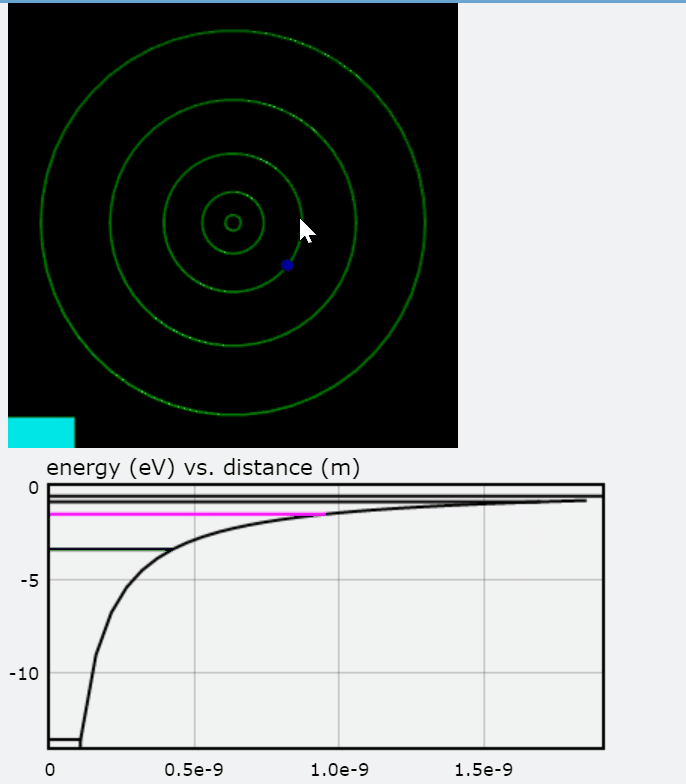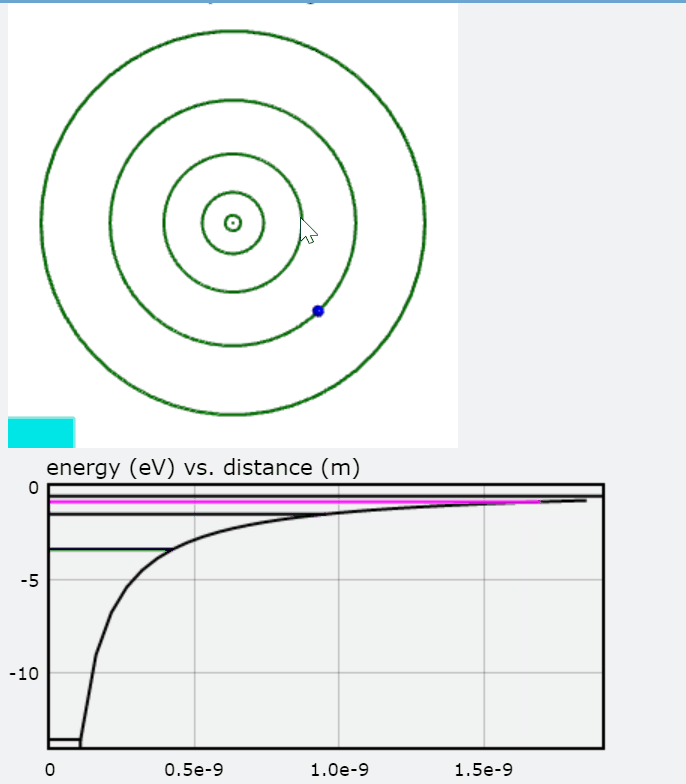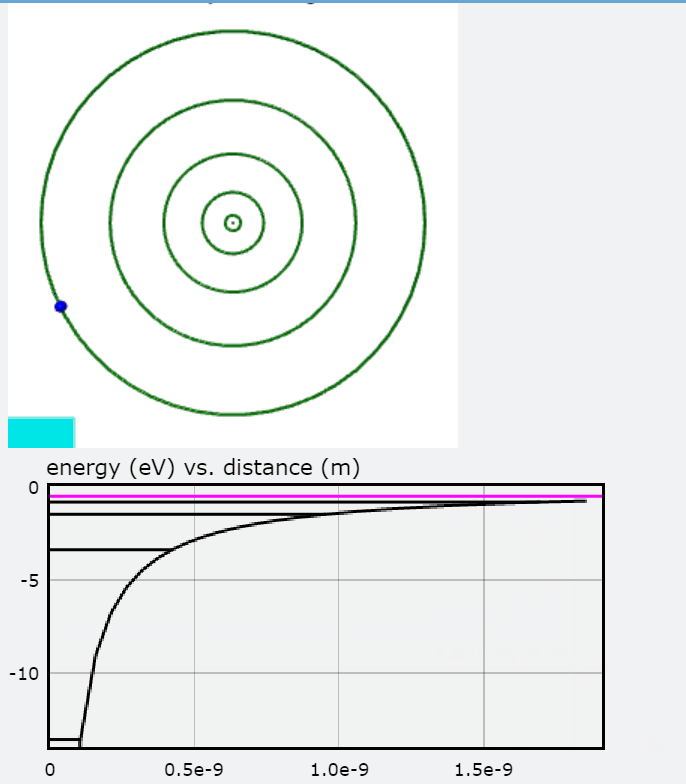
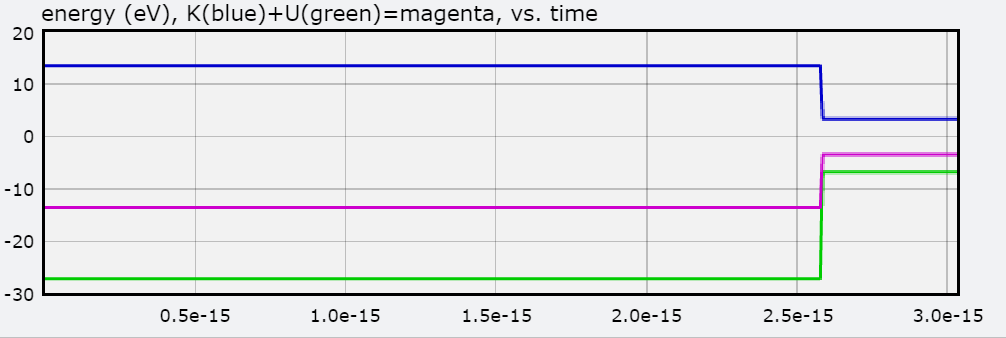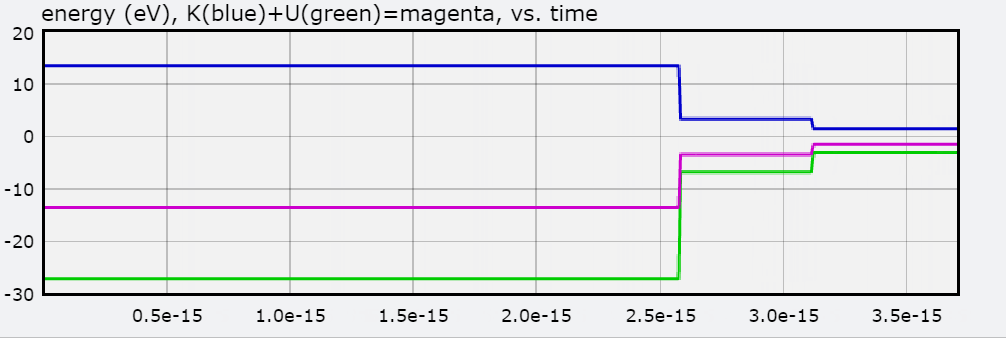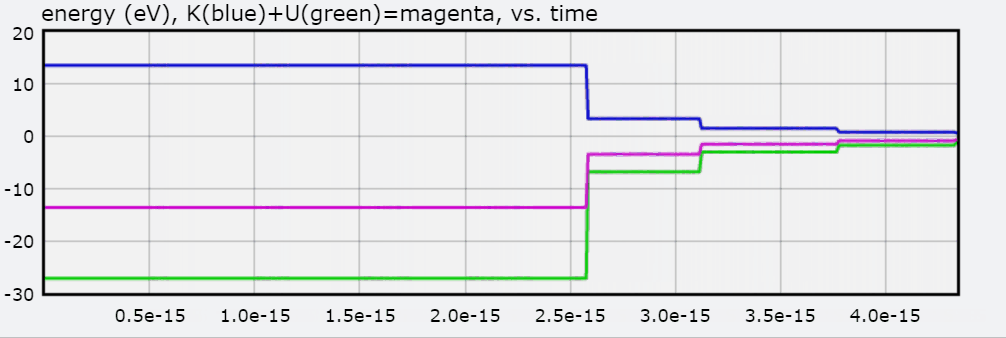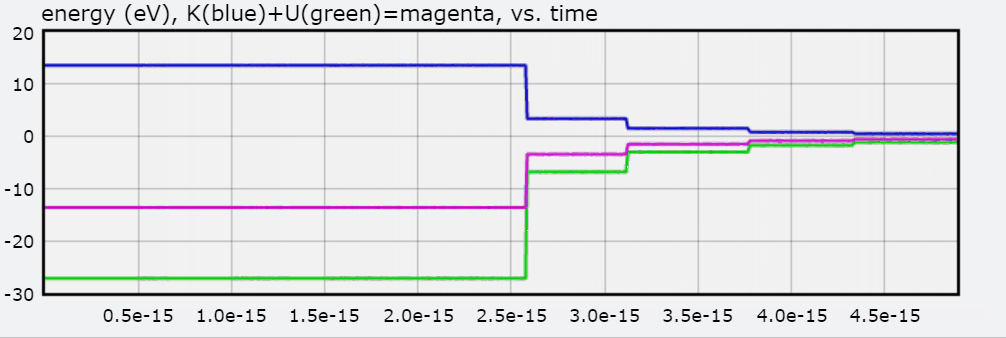
In this visualization, an electron in orbit around a hydrogen nucleus progresses upwards though the available energy levels of the Bohr Model. The accompanying graph highlights the energy corresponding to each orbit with respect to the distance between the electron and the hydrogen nucleus. The greater the distance, the less negative the electron's energy and thus the less energy that must be added to free the electron from its orbit. To interact with this glowscript visualization of the Bohr Model, click here.

You will also find a graph of Total Energy (eV), Kinetic Energy, and Potential Energy, with each jump representing the electron transitioning to an orbit.

PhET additionally provides an effective "Models of the Hydrogen Atom" simulation that compares the various predictive models including the Bohr model. Further, it employs absorption and compares the models to the experimental results. The link is provided below for further evaluation.

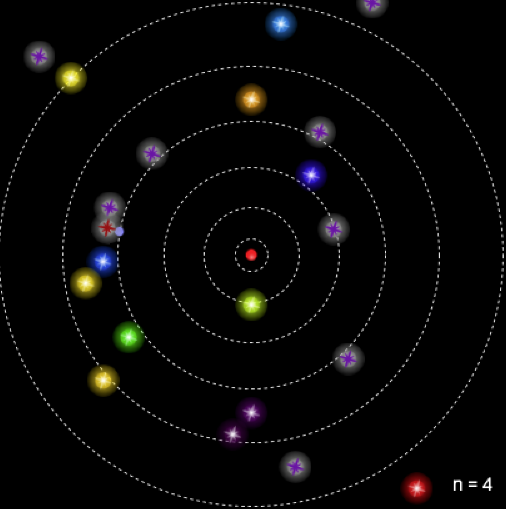
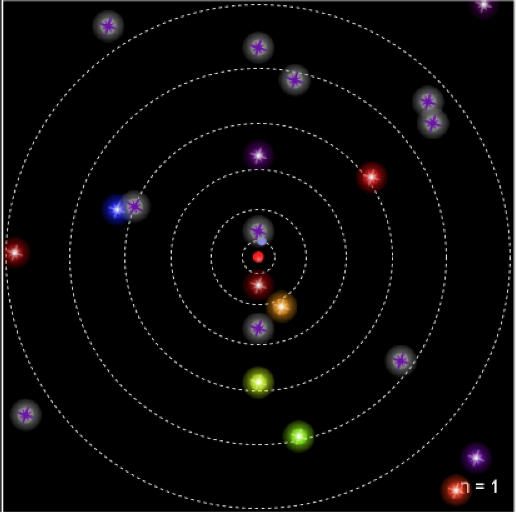
https://phet.colorado.edu/sims/cheerpj/hydrogen-atom/latest/hydrogen-atom.html?simulation=hydrogen-atom

The images above are stills taken from the PhET simulation. As the electron absorbs energy, it will move to a higher orbit (energy level), and when it drops back to the steady-state, it releases photon(s).

Examples

Simple

Find the magnitude of the translational angular momentum of an electron when a hydrogen atom is in its 2nd excited state above the ground state.

--

We know that the only possible states of the hydrogen atom are those when the electron's translational angular momentum is an integer multiple of ħ. [math]\displaystyle{ |\vec L_{trans,c}| = Nħ }[/math] For the 2nd excited state, N = 3 Now just plug the numbers in [math]\displaystyle{ |\vec L_{trans,c}| = (3)(1.05*10^{-34} J*s) = 3.15*10^{-34} J*s }[/math]

Middling

[6]A hydrogen atom is in state N = 3. Assuming N = 1 is the lowest energy state, calculate the K+U (energy of electron) in electron volts for this atomic hydrogen energy state.

1) [math]\displaystyle{ E(3) = {\frac{-13.6 eV}{3^2}} }[/math] = -1.51 Joules

2) [math]\displaystyle{ E(1) = {\frac{-13.6 eV}{1^2}} }[/math] = -13.6 Joules

3) K+U (a sum of the kinetic energy and the potential electromagnetic energy of the photon) = energy of photon = [math]\displaystyle{ E(1) - E(3) = {\frac{-13.6 eV}{3^2}} - {\frac{-13.6 eV}{1^2}} }[/math] = 12.09 Joules

Below is the graph of E as the hydrogen atom goes from N = 3 to N = 1.

Difficult

Hydrogen has been detected transitioning from the 101^st to the 100^th energy levels. What is the wavelength of the radiation emitted from this transition? Where in the electromagnetic spectrum is this emission?

To solve this problem, we first need to use formulas derived from Bohr Model of hydrogen atom. It is [math]\displaystyle{ E = {\frac{-13.6 eV}{N^2}} }[/math]

Then solve for the wavelength using formula from Electromagnetic Wave Theory.

This wavelength falls in the microwave portion of the electromagnetic spectrum.

Connectedness

1. I chose this topic because I have unintentional conducted research on it outside of a classroom environment that was driven by a question that I have asked myself for as long as I can remember: What is light? I couldn't touch it, I couldn't produce it myself, and I could not explain where light comes from. I am so thankful that I grew up in the time where a) I could hop on the internet to see if there was an answer to my question and b) that the answer exists. We know what light is: photons of a wavelength in the visible spectrum, and we know where light comes from: energy released by electrons dropping in levels of orbit. I loved the introductory internet research I did on this subject, and it introduced me to the bizarre world of quantum physics, which I continue to be puzzled by and curious about. I also chose this topic because of my admiration for the man behind it, Niels Bohr. He was a man on the cutting edge of science who pushed our understanding of the universe by leaps and bounds by unveiling aspects of the microscopic universe.

2. As an industrial engineering major, it is pretty difficult to quantify how a concept of physics, especially one as specific and complex as Bohr's atomic model, will directly connect to my major. This should not stop me from seeking knowledge about it to possess a more well rounded knowledge of the world. Still, it isn't hard to find applications. If I am working to optimize the production of a laser engraving facility, for example, having an understanding of the basic dynamics behind the lasers and machinery will help me to have a more level conversation with the engineers developing and maintaining the lasers, and will prevent any massive rifts of understanding between the engineering side of the facility with the men working on the business end of the operation.

3. The industrial application of the concepts covered on this page are enormous in today's day and age. We are in the midst of an energy revolution, with solar energy looking to replace fossil fuels as the primary source of energy to the world. Understanding the energy of photons and light waves emitted from the sun is essential to the ongoing process making solar energy a more cost effective alternative to traditional fossil fuels. Once this optimization occurs, the planet will have a new primary source of energy with cleanliness and availability that is absolutely unprecedented.

History

Plum pudding model, which Rutherford's model expanded on.

To understand how revolutionary Bohr's theories and advancements were, one must have a general understanding of the accepted atomic model at the time, the Rutherford model. The Rutherford model was created in 1911 by New Zealand born chemist Ernest Rutherford. The dominant model for the structure of the atom before Rutherford's breakthrough, was the plum pudding model. While this model correctly surmised that atoms are constructed from constituents of both positive and negative charge and that the negatively charged components were quite small relative to the atom, the plum pudding model depicted electrons as stationary, lodged in place in a substance believed to constitute most of the space an atom occupies.

After conducting one of the most famous experiments in the world of physics, the Geiger-Marsden experiment, more commonly known as the gold foil experiment, Rutherford realized that the majority of the atom is empty space with the mass of the atom existing predominantly in a small volume in the center of the atom. Thus, Rutherford is credited with the discovery of the atomic nucleus. Despite its numerous breakthroughs, the Rutherford model was neither perfect nor complete. Rutherford proposed that the emission spectrum of hydrogen would look more like a smear rather than being made up of distinct lines. However, this was flawed, as it suggested that atoms can emit energy that isn't quantized. [8]

Rutherford's model of the atom, which Bohr expanded on.

Niels Bohr, a physicist from Denmark, was able to explain the true nature of electrons by improving on the Rutherford model of the atom. In 1911 Bohr traveled to England in order to study the structure of atoms and molecules. There, he attended lectures on electromagnetism and worked with Rutherford and other scientists such as J. J. Thomson. When he returned to Denmark in 1912, Bohr noticed that in the atomic emissions spectrum of hydrogen, only certain colors could be seen. Thus, he theorized that electrons need to be in energy levels that are quantized. He related the energies of the colors he saw to the differences of hydrogen's energy levels. Although this model is not entirely correct, as it only applies to systems where two charged particles orbit each other, it still has many features that are very applicable to physics today. Later on, scientists such as Werner Heisenberg and Erwin Schrödinger worked to improve upon this model.[9]

Shortcomings of the Bohr Model

While the Bohr model is an important predecessor to the current quantum mechanical models of the atom, it doesn't correctly describe some aspects of electron orbitals. It does not provide any reasoning as to why certain spectral lines are brighter than others. Its main shortcoming is that it violates the uncertainty principle, as it considers electrons to have a definite radius and momentum, not considering more advanced quantum theories and properties that have been discovered since the Bohr first theorized the model. This model is very basic, and in order to know more specific details about spectra and charge distribution, more calculations must be done. Many of the failures of the Bohr model can be corrected by the Schrodinger equation for the hydrogen atom. Normalized wavefunctions and their series typically include the value of the first Bohr's radius as a reference point. 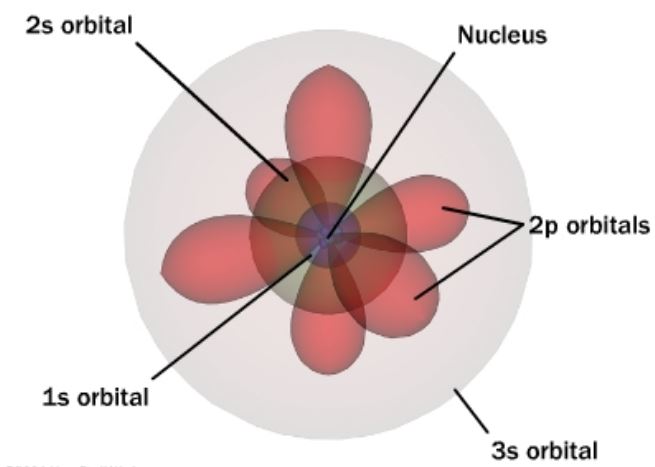For example, the R(r) component of the Hydrogen Separated Equation Solution for n=1, 1s is [math]\displaystyle{ \frac{2e\lt sup\gt -r/a\lt sub\gt 0\lt /sub\gt }{a\lt sub\gt 0\lt /sub\gt \lt sup\gt 3/2\lt /sup\gt }[/math] The current working model of the atom is the quantum mechanical model of the atom, which displays the electron orbit shapes very different from the orbits of the solar system and accounts for the fact that the electrons do not exist in one specific location in the orbit, but rather exists at many certain locations in the orbital as probabilities and frequencies. See the picture below for a visual representation of this quantum mechanical atomic model.

[2] [3] [4] [5] [6] [7] [8] [9] [10] [11] Note: All images on this page are either free for commercial use (with no attribution required) or made by myself.