Atomic Structure of Magnets
Claimed by Stepan Shabalin (Spring 2025).
Sarah Ghalayini (Fall 2017)
Logan Vaupel (Fall 2016)
Magnets generate their magnetic fields at the atomic level.
The Main Idea
The magnetic field produced by a magnet is the sum of the magnetic dipole moments generated by each individual atom. These very small magnetic fields are generated much like those of circular current loops; however instead of being generated by electrons or charges flowing through a wire, the field in each individual atom is produced in one three different ways:
- An electron orbiting around the atomic nucleus. (See Figure 1)
- An electron rotating around its axis. (See Figure 1)
- The rotation of protons and neutrons within the nucleus of the atom.
All three of these situations produce a magnetic dipole proportional to the angular momentum. Together, the magnetic dipoles of all the atoms in the magnet sum to give the total magnetic dipole of the magnet. The magnetic field at an observation location can then be found from this dipole.
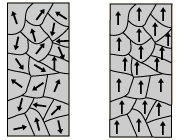A non-magnetic material (left) and a magnetic material (right). In the non-magnetic material, the atomic magnetic dipoles are random, and average out to zero. In the magnetic material, the magnetic field from the atomic magnetic dipoles are aligned, which allow for a nonzero magnetic field. Image retrieved from Hyperphysics]], free for educational use.
Although all atoms have electrons orbiting their nuclei, most materials are not magnetic. Each atom in these materials has a small magnetic dipole, however these dipoles are generally disordered and therefore the orbital and spin motions do not line up. Thus, the net magnetic field of each region throughout the material sums to zero. In magnetic materials, however, regions of magnetic dipoles line up enough to produce a significant magnetic field. Although some of these regions cancel other regions out, enough regions align to produce a nonzero magnet field. Such materials are called "ferromagnetic." This is allowed by interactions between atoms in certain elements (usually iron, nickel, cobalt, or alloys of these metals).
A material such as iron can be seen as a collage of different regions of nearly perfect alignment and net magnetic field. Normally, these regions are oriented at random relative to one another and do not produce a net magnetic field. But in the presence of a strong external magnetic field, such as one from a solenoid, the regions within the material that are already aligned with that external field will multiply in strength, creating a much larger net magnetic dipole moment within the formerly non-magnetic piece of iron. When the external field is removed, however, the iron returns to approximately the same net magnetic dipole as before the field was applied. But in the presence of a large enough external field, within certain non-pure alloys of iron, the internal regions can rotate and align enough to create a more permanent change in the material that remains after the external field is removed. This is called a permanent magnet, which you can probably find holding up your finger-paintings on your refrigerator at home. However, beating up the magnet with some hard blows or jolts can cause the regions to misalign, destroying the magnetic dipole. Heating the material above a certain temperature can produce the same effect.
To better understand why some materials better align to form magnets while others do not requires more in-depth knowledge of quantum mechanics, which is certainly interesting but not discussed here (so that your head doesn't explode from the concentrated sheer mind-blowing awesomeness of pure physics). Essentially, the alignment comes from electric interactions between atoms, not so much the weaker magnetic ones. For more information, see "Further Reading" below.
A Mathematical Model
We can model the magnetic dipole moment of a magnet by comparing the movement of electrons about the nucleus to the movement of current in a loop. In a current loop [math]\displaystyle{ {\mu = I \pi R^2} }[/math] when [math]\displaystyle{ R }[/math] is the radius of the loop. Since the units of [math]\displaystyle{ I }[/math] are [math]\displaystyle{ \frac{charge}{time} }[/math], the charge of an electron is [math]\displaystyle{ -e }[/math], and the period for one orbit around the nuclues is [math]\displaystyle{ t = \frac{2 \pi R}{v} }[/math] where [math]\displaystyle{ v }[/math] is the speed of the the electron, the magnetic dipole for one atom in a magnet simplifies to [math]\displaystyle{ \mu = \frac{e R v}{2} }[/math] where [math]\displaystyle{ R }[/math] is now the radius of the orbit.
The magnetic dipole is proportional to the angular momentum, [math]\displaystyle{ L }[/math] of the electron orbiting the nucleus. Assuming a circular orbit and assuming the speed of the electron is much less than the speed of light, [math]\displaystyle{ L = R p = R m v }[/math]. Multiplying the magnetic dipole by [math]\displaystyle{ \frac{m}{m} }[/math] reveals the proportionality of magnetic dipole and angular momentum [math]\displaystyle{ \mu = \frac{m}{m} \frac{e R v}{2} \Rightarrow \mu = \frac{e}{2 m} (R m v) = \frac{e}{2 m} L }[/math] From this equation the charge and mass of an electron and a proton can be plugged in to be compared. Because an electron weighs so much less than a proton, the magnetic dipole from the orbit of an electron is [math]\displaystyle{ 10^4 }[/math] times bigger than the magnetic dipole from the rotation of a proton or neutron in the nucleus, allowing the contributions from the protons and neutrons to be neglected.
For the purpose of calculating the magnetic dipole, it can be assumed that [math]\displaystyle{ L }[/math] is equal to Planck's Constant, [math]\displaystyle{ \hbar = 6.626 \times 10^{-34} \, J \cdot s }[/math]. Plugging in the charge and mass of an electron gives [math]\displaystyle{ \mu \approx 5.81 \times 10^{-23} \, A \cdot m^2 \, per \, atom }[/math].
Finally, if [math]\displaystyle{ \mu = N \mu_{atom} }[/math] where [math]\displaystyle{ N }[/math] is the number of atoms, this [math]\displaystyle{ \mu }[/math] is the magnetic dipole of the magnet.
However, it is worth noting that we made several simplifying assumptions to create this model. First, we assumed that the movement of electrons in their orbitals were moving in a circular path, creating angular momentum. In reality, atomic orbitals are much more complex probability distributions for finding an electron at a specific location. The different energy levels of electron orbits form different shapes with different angular momentums. The "s" orbital is a sphere with a net zero angular momentum, while the "p, d, and f" orbitals are asymmetrical and thus produce an angular momentum, which can produce a magnetic dipole moment. Also, we assumed that there was only one unpaired electron moving within its orbit per atom, when in reality, many materials, such as iron, have two or more unpaired electrons that contribute to the net magnetic dipole moment. A more accurate model would also take into account not just the magnetic contribution of individual atoms, but also how they impact one another. We also assumed that the atoms were perfectly aligned, when this would most certainly never happen in reality. Our modern understanding of magnets also suggests that the axial spinning of electrons contributes a great deal to the overall magnetic dipole moment, in comparison to the orbital angular momentum. Thus, a more accurate model would produce far more complex calculations. Nevertheless, this simpler model still gives useful insight into how the movement of electrons within atomic orbitals within a material can create a macro magnetic dipole effect.
A Computational Model
Here is a link that to glowscript showing a model of an electron orbiting a nucleus, which is how the magnetic dipole in a magnet is formed.
Examples
Simple
A bar magnet made from iron has a mass of 72 g. What is the magnetic dipole of the bar magnet?
[math]\displaystyle{ N = \left (\frac{72 \, g \, iron}{56 \, \frac{g \, iron}{mol \, iron}} \right ) \left (6.022 \times 10^{23} \frac{atoms}{mol} \right ) = 7.74 \times 10^{23} \, atoms }[/math]
[math]\displaystyle{ \mu = (7.74 \times 10^{23} \, atoms) \left (5.81 \times 10^{-23} \, \frac{A \cdot m^2}{atom} \right ) = 44.97 \, A \cdot m^2 }[/math]
Middling
A bar magnet that is 15% mass iron and 85% mass nickel has a mass of 126 g. What is the magnetic dipole of the bar magnet?
[math]\displaystyle{ 126 \, g \cdot 0.15 = 18.9 \, g \, iron }[/math]
[math]\displaystyle{ 126 \, g \cdot 0.85 = 107.1 \, g \, nickel }[/math]
[math]\displaystyle{ N = \left (\frac{18.9 \, g \, iron}{56 \, \frac{g \, iron}{mol \, iron}} \right ) \left (6.022 \times 10^{23} \frac{atoms}{mol} \right ) = 2.03 \times 10^{23} \, atoms }[/math]
[math]\displaystyle{ N = \left (\frac{107.1 \, g \, nickel}{59 \, \frac{g \, nickel}{mol \, iron}} \right ) \left (6.022 \times 10^{23} \frac{atoms}{mol} \right ) = 1.09 \times 10^{24} \, atoms }[/math]
[math]\displaystyle{ 2.03 \times 10^{23} \, atoms + 1.09 \times 10^{24} \, atoms = 1.29 \times 10^{24} \, atoms }[/math]
[math]\displaystyle{ \mu = (1.29 \times 10^{24} \, atoms) \left (5.81 \times 10^{-23} \, \frac{A \cdot m^2}{atom} \right ) = 74.95 \, A \cdot m^2 }[/math]
Difficult
A compass originally points north. A bar magnet made of iron is placed [math]\displaystyle{ 20 \, cm }[/math] west of the compass on axis, with the north end of the magnet pointing towards the compass. The compass deflects [math]\displaystyle{ 55^\circ }[/math]. What is the mass of the magnet?
[math]\displaystyle{ \overrightarrow{B}_{net} = \overrightarrow{B}_{Earth} + \overrightarrow{B}_{magnet} }[/math]
[math]\displaystyle{ B_{magnet} = (2 \times 10^{-5} \,T) \tan{55^\circ} }[/math]
[math]\displaystyle{ B_{magnet} = 2.86 \times 10^{-5} \,T }[/math]
[math]\displaystyle{ B_{magnet} = \frac{\mu_0}{4 \pi} \frac{2 \mu}{r^3} }[/math]
[math]\displaystyle{ \mu = \frac{r^3 B_{magnet}}{2} \frac{4 \pi}{\mu_0} }[/math]
[math]\displaystyle{ \mu = \frac{(0.20 \, m)^3 (2.86 \times 10^{-5} \,T)}{2} \left (1 \times 10^7 \, T \cdot \frac{m}{A} \right) }[/math]
[math]\displaystyle{ \mu = 1.14 \, A \cdot m^2 }[/math]
[math]\displaystyle{ number \, of \, atoms = \frac{1.14 \, A \cdot m^2}{5.81 \times 10^{-23} \, \frac{A \cdot m^2}{atom}} }[/math]
[math]\displaystyle{ number \, of \, atoms = 1.96 \times 10^{22} \, atoms }[/math]
[math]\displaystyle{ mass \, of \, bar = (1.96 \times 10^{22} \, atoms) \left ( \frac{56 \, \frac{g \, iron}{mol \, iron}}{6.022 \times 10^{23} \frac{atoms}{mol}} \right ) }[/math]
[math]\displaystyle{ mass \, of \, bar = 1.82 \, g \, iron }[/math]
Connectedness
- How is this topic connected to something that you are interested in?
- Magnets are a classic toy given to children as an introduction to science, and I was no exception. I have fond memories making magnet models and playing with buckyballs, and remember how fascinated I was with how the magnets interacted with one another. What made them attract and repel one another at such far distances? This makes it all the more satisfying to learn more about how they work on a fundamental level.
- How is it connected to your major?
- A solid understanding of the structure of an atom and the resulting physical properties of a material are central to chemistry. Potential applications are endless and applicable to many disciplines including materials science where one might design an alloy for a product that is paramagnetic and can be used with a permanent magnet to design a product, such as a purse latch.
- Is there an interesting industrial application?
- Most certainly. If you understand how certain materials act in the presence of a magnetic field, you can incorporate that the into product design, as well as the processing stage when preparing that material. This is obvious in the automotive industry, but even in medicine and bioengineering an understanding of biomaterials is very helpful. This is especially helpful in designing prosthetics where it will be inconvenient and impractical if the product is magnetic.
History
The "first" magnets were called lodestones and are just naturally magnetic pieces of metal. There are records of lodestones dating up to 2500 years ago from all over the world. By the 12th century, humans discovered they could suspend small pieces of lodestones which would allow them to rotate, and then used them for navigation. We still use compasses to this day!
Applications
An Unexpected Discovery
In World War II, United States ships were equipped with magnetic field detection devices to scan for enemy submarines in the Atlantic. They discovered alternating bands of N-S and S-N oriented magnetic dipoles that ran parallel to the long ridges along the seafloor. This led physicists, geologists, and another science geeks to determine that as the iron-rich molten rock that comes up from the mantle during seafloor spreading of tectonic plates cools, iron fragments align with the earth's magnetic field, creating a magnetic dipole. The alternating bands indicates that the orientation of the earth's magnetic field reverses approximately 4 to 5 times per 100 million years. This gives valuable insight into the speed of seafloor spreading, as well as the long term history and behavior of plate tectonic interactions. If you don't believe me, check out this short video: Magnetic Mineral Alignment and WWII
Magnetic Resonance Imaging
MRI (Magnetic Resonance Imaging), as you all probably know, is a medical imaging technology that works by putting some really strong magnets near your body. It is safer than CT (Computational Tomography) because it doesn't need to shoot high-energy high-frequency rays into your body. Unlike CT, it doesn't image dense (high attenuation) objects, but hydrogen atoms. It can be used to take 3D volumetric images of various parts of your body, and, more interestingly, the brain. Depending on the parameters (more on this later), MRI can diagnose various diseases such as strokes and tumors. It has non-clinical applications in psychology, too: functional MRI, the type that looks at blood flow in various vessels of the brain, can even be used to read minds!
MRI is a specialized application of 'Nuclear Magnetic Resonance (NMR). This is a different technology from the one that was used to detect submarines during WWII, and is based on advances in quantum physics. The exact explanation for how it works is a few years above the level of this course, but I will try to summarize it without wild inaccuracies.
An MRI machine has a large superconducting magnet that creates a magnetic field, two coils that produce radio waves and a receiver. MRI works by producing two magnetic pulses which affect (in a way I will explain below) hydrogen atoms and recording the echo radio waves the atoms' nuclei emit afterwards.
There are many incorrect explanations of MRI online (see "Is Quantum Mechanics necessary for understanding Magnetic Resonance?" (IQMNFUMR)). The inaccuracies begin with the first step of the process: applying the constant magnetic field. It is typically claimed that the field makes protons, the thing that we care about, can be approximated as small magnets, and that they align with the magnetic field in the same way that magnets align with the Earth's magnetic field.
Firstly, are hydrogen atoms small magnets? You may have heard the explanation in lecture that atoms are magnets because they have electrons orbiting nuclei, which is a constant flow of current going in a loop, which obviously produces a dipole. However, if you think about it, it stops making sense: we rarely see hydrogen atoms (H) on their own; they will be part of H2O or H2, which doesn't intuitively seem to have those properties. What actually gives hydrogen atoms magnetic properties is an inherent quantity called spin that elementary particles like protons have. See this resource for a detailed explanation of spin in the context of MRI. Hydrogen is the one element with a nucleus whose spin is not cancelled out on the net that is abundant in the human body. Spin is similar to classical angular momentum, and its magnitude can change depending on the energy level of the particle.
The previous sentence is incorrect: spin isn't a 3D vector like angular momentum, but instead is a probability distribution on those 3D vectors parametrized by two complex numbers. IQMNFUMR doesn't explain the specifics, and you should take a QM course if you want to learn them. We will try to give a classical explanation of spin in the rest of this section.
Secondly, do magnets align with the Earth's magnetic field? Actually, by all means, they shouldn't: if you place a bar magnet into a uniform magnetic field and keep its position fixed, it will keep spinning around the axis of the direction of the external magnetic field. See this trinket for a visualization. This happens because the magnetic torque can be expressed as:
[math]\displaystyle{ \tau = \mu \times B }[/math]
Where [math]\displaystyle{ \mu }[/math] is the current spin and B is the external magnetic field. So, what this means is that the spin will rotate along a ring offset along the B axis, because the velocity at every point is orthogonal to both the current spin and B. It can easily be seen that the velocity and thus the frequency of the precession is proportional to B (this will be important later!).
But then why do compasses work? I found two explanations online: it's either because the motion is restricted to a plane (two axes) or because the fluid in a compass creates drag that dampens the motions of the arrow:
[math]\displaystyle{ \tau_{drag} = \mu \times \frac{d \mu}{dt} }[/math]
I tested the drag explanation here. It works really well, probably because the drag direction is pointed down away from B by the right hand rule. The axis restriction one doesn't work as well.
This explanation sounds good and introduces the important principle of precession, but it is utterly irrelevant to protons because they don't experience damping like compasses are designed to. The real explanation of what happens to protons in a magnetic field requires quite a bit of quantum mechanics and thermodynamics. We explained before that spin is probabilistic; what this means is that until you sample it, all of the possibilities for its values evolve together. Once you sample it, it points either in the direction of or against the external magnetic field. This has been confused with the compass metaphor to create the picture that the protons all point in the direction of or against the magnet when that is simply untrue. Before the radio frequency pulses are applied, the spins are precessing while pointing in random directions.
The explanation above is incomplete. In addition to the precession, the spin of protons is affected by random thermal motion of the molecules; this thermal motion walks around the Boltzmann distribution, which means the spin is more likely to switch to a lower energy state tan a higher energy one. Overall, the spin will lose energy, which makes it point either to or away from the external magnetic field. In the end, the spins are somewhat more likely to align with the magnetic field than oppose it. This creates a net magnetization pointed in the direction of the magnetic field.
What are the radio frequency pulses mentioned in the explanation of spin in the presence of a magnetic field? Recall that there are two coils in the MRI machine. Taking an image requires creating an electromagnetic wave at a frequency that matches the one that all the nuclei are precessing over. A magnetic field that travels in space and changes direction over time at the same frequency the precessing is rotating (see the "Pulsed Magnetic Fields" section of The Basics of MRI) will resonate with the precession in a way that lets us rotate all nuclei at a constant rate. If we are very precise with our timing and stop the pulse after a few microseconds, we can rotate the nuclei by exactly 90 or 180 degrees. I haven't managed to get this to work in a Trinket, but the math seems persuasive.
So, we have nuclei with a small average bias in the direction of the external magnetic field, we can rotate them by 90 degrees. What do we do next? Nothing. Once we stop the magnetic pulse, the nuclei will continue precessing and eventually regain the original distribution with the barely-noticeable orientation towards the external magnetic field. We can model the rate at which the situation becomes normal using variables called T1 and T2. What is important is that for a brief time, the net magnetic field is rotated by 90 degrees and is entirely in the plane orthogonal to the external magnetic field (the transverse plane). The precession in the transverse plane will produce magnetic waves and can be captured with the receiver. But what is the use of the received signal? It seems like there's no way to localize where the nuclei are just from the sum of the signals they emit.
And you are right! This is where the second coil comes in. While the first produces an RF pulse, the second creates a slight magnetic field gradient which makes the external magnetic field vary slightly at different points in space. This variance means that the precession frequencies also vary slightly (remember the frequency is proportional to field strength!). This means that they will precess at different frequencies inside the transverse plane and relay signals of different frequencies to the receiver. If we can find the intensity of the received signal at all frequencies, we can find the density at all slices along one axis. We can find the intensity with a Fourier transform, which is complicated to explain but is the perfect algorithm for this. See Basics of MRI for more. Once we can find the density along one axis, we can make 2D scans by rotating the axis in a plane and combining observations along all axes using the Radon transform. These details aren't as interesting because they're more CS than physics and you can learn how they work in a few minutes.
These are the basics. There are a lot of improvements to be made upon this including a way to scan in 3D, more details of the quantum mechanics of why this works, and you can look at the sources for information on that.
This section doesn't have as many illustrations as I'd like because I failed to replicate some of the experiments and image uploading doesn't seem to work at this time. It is short, but I spent more than 5 hours on research. Feel free to extend this.
See also
The Angular Momentum Principle
Further reading
VIDEO: Magnetism and Quantum Mechanics
"Is Quantum Mechanics Necessary for Understanding Magnetic Resonance?" (PDF)
External links
References
Chabay, R., & Sherwood, B. (2015). Magnetic Field. In Matter & interactions (4th ed., Vol. 2, pp. 693-698). Hoboken, NJ: Wiley.
Ferromagnetism. (n.d.). Retrieved December 5, 2015, from http://hyperphysics.phy-astr.gsu.edu/hbase/solids/ferro.html#c4
Lodestone. (n.d.). Retrieved December 5, 2015, from https://en.wikipedia.org/wiki/Lodestone
Origin of Magnetism. (n.d.). Retrieved December 5, 2015, from http://www.gitam.edu/eresource/Engg_Phys/semester_2/magnetic/intro.htm