Magnetic Dipole Moment

From Physics Book
Jump to navigation Jump to search

'

Main Idea

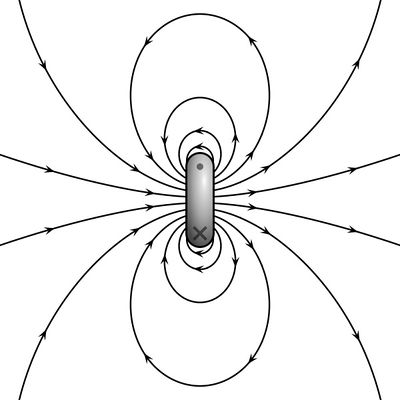
The magnetic dipole moment of a loop of current may be considered to be a measure of the strength of the magnetic field. The magnetic field generated by a magnet points from south to north and is proportional to its magnetic dipole moment. In a loop of current, the magnetic dipole moment is a vector that is perpendicular to the loop and can be found using the right-hand-rule. The magnetic dipole moment is a measure of the strength of the magnetic dipole.

The main idea for this topic is to define the magnetic dipole moment and distinguish from the magnetic moment. The magnetic moment is a vector quantity that is used to calculate the torque generated by a magnetic field while the magnetic dipole moment is a value used to define the current of a loop to find the magnetic field on axis.

The magnetic dipole moment can be thought of as a compass needle. When there is an external magnetic field, a current-carrying loop will rotate to align the magnetic dipole moment along the magnetic field.

Mathematical Model

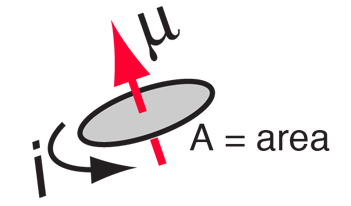
The magnetic dipole moment is represented by a vector [math]\displaystyle{ \mathbf{µ} }[/math]. The magnitude of this is set equal to the current running through the wire multiplied by the area of the circular loop the current runs through. Here the area of the circular loop is defined as [math]\displaystyle{ \pi R^2 }[/math]. Its direction is determined by the right hand rule. The units for the magnetic dipole moment are amperes times meters squared:

[math]\displaystyle{ |\boldsymbol{ \mu }| = \mu = I A = I \cdot \pi R^2 }[/math]

A coil of [math]\displaystyle{ N }[/math] current loops would thus have a magnetic moment of:

[math]\displaystyle{ |\boldsymbol{\mu}| = \mu = N I A }[/math]
  • The equation for the magnitude of the magnetic field at the center of a current loop simplifies as (See Magnetic Field of a Loop):
[math]\displaystyle{ \begin{align} B & = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{(z^2 + R^2)^{3/2}} \text{, where } z = 0 \\ & = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{R^3} \text{, and the } R^2 \text{ cancels} \\ & = \frac{\mu_0}{4 \pi} \frac{2 \pi I}{R} \\ & = \frac{\mu_0}{4 \pi} \frac{2 \pi \frac{\mu}{\pi R^2}}{R} \text{, where } I = \frac{\mu}{\pi R^2} \\ B & = \frac{\mu_0}{4 \pi} \frac{2 \mu}{R^3} \ \mathbf{(2)}\\ \end{align} }[/math]
  • The magnitude of the magnetic moment [math]\displaystyle{ \mu }[/math] of an electron in circular orbit is given by:
[math]\displaystyle{ |\boldsymbol{\mu}| = \mu = I A = - \frac{e}{2m_{e}} L }[/math]
[math]\displaystyle{ L }[/math] is the magnitude of the angular momentum of the electron
  • The torque experienced by a current loop due to an external magnetic field is defined as the cross product of the magnetic dipole moment of the loop and the external magnetic field applied to the loop:
[math]\displaystyle{ \boldsymbol{\tau} = \boldsymbol{\mu} \times \boldsymbol{B} }[/math]
  • The magnetic potential energy of the loop is also defined as the negated dot product between the magnetic dipole moment of the loop and the external magnetic field applied to the loop:
[math]\displaystyle{ U(\theta) = - \boldsymbol{\mu} \bullet \mathbf{B} = - [\mu B] \ \text{cos}(\theta) }[/math]
[math]\displaystyle{ \theta }[/math] is the angle between the magnetic moment and the external magnetic field
  • For example, if [math]\displaystyle{ \theta = 0° }[/math], then we see:
[math]\displaystyle{ U(0°) = -[\mu B] \ \text{cos}(0°) = -\mu B }[/math]
  • For [math]\displaystyle{ \theta = 180° }[/math], we get:
[math]\displaystyle{ U(180°) = -[\mu B] \ \text{cos}(180°) = \mu B }[/math]
From this we see that, when there is no separation between the magnetic field's direction and the magnetic moment's direction, the loop is at its lowest possible magnetic potential energy state, and when the directions are anti-parallel, the loop is at its highest possible magnetic potential energy state, as shown in the figure.

Computational Model

Insert Computational Model here

Examples

Simple

A [math]\displaystyle{ 1,200 }[/math] turn circular coil of radius [math]\displaystyle{ 10 \text{ cm} }[/math] carries [math]\displaystyle{ 2 \text{ Amps} }[/math].

a) What is the magnitude of the magnetic dipole moment of the coil. What direction does it point?
We can use our Mathematical Model to answer this:
[math]\displaystyle{ \mu = N I A = N I \cdot \pi R^2 }[/math]
In this problem, the following values have been specified for us:
[math]\displaystyle{ N = 1,200 \text{ turns or loops} }[/math]
[math]\displaystyle{ R = 0.1 \text{ m} }[/math]
[math]\displaystyle{ I = 2 \text{ Amps} }[/math]
Therefore, [math]\displaystyle{ \mu }[/math] is:
[math]\displaystyle{ \mu = 1,200 \times 2 \times \pi \times (0.1)^2 = 75.4 \text{ A} \cdot \text{m}^2 }[/math]

Middling

A current loop with a radius of [math]\displaystyle{ 2 \text{ m} }[/math] and a current of [math]\displaystyle{ 5 \text{ Amps} }[/math] is in an external magnetic field. This magnetic field is given by:

[math]\displaystyle{ \mathbf{B_{ext}} = (x, y, z) = (1, 1, 1) = \sqrt{3} \left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right) }[/math]

A unit vector normal to the area of the current loop (and has a direction consistent with the right-hand rule) is given by:

[math]\displaystyle{ \mathbf{\hat n} = (x, y, z) = \left(-\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}\right) }[/math]
a) What is the magnetic potential energy of the current loop?
The magnetic potential energy of a current loop is defined as:
[math]\displaystyle{ U(\theta) = - \boldsymbol{\mu} \bullet \mathbf{B_{ext}} = - [\mu B_{ext}] \ \text{cos}(\theta) \ \mathbf{(1)} }[/math]
Since [math]\displaystyle{ \mathbf{\hat n} }[/math] is consistent with the direction of [math]\displaystyle{ \boldsymbol{\mu} }[/math] and has a magnitude of [math]\displaystyle{ 1 }[/math], we can define [math]\displaystyle{ \boldsymbol{\mu} }[/math] as the its magnitude times its unit direction:
[math]\displaystyle{ \boldsymbol{\mu} = \mu \mathbf{\hat n} \ \mathbf{(2)} }[/math]
We know [math]\displaystyle{ \mu }[/math] is:
[math]\displaystyle{ \mu = I A = I \cdot \pi R^2 \ \mathbf{(3)} }[/math]
Putting 2 and 3 together shows:
[math]\displaystyle{ \boldsymbol{\mu} = \left( I \cdot \pi R^2 \right) \mathbf{\hat n} }[/math]
Plugging this into 1 gives:
[math]\displaystyle{ U(\theta) = - \left( I \cdot \pi R^2 \right) \mathbf{\hat n} \bullet \mathbf{B_{ext}} }[/math]
The dot product is calculated as:
[math]\displaystyle{ \begin{align} \mathbf{\hat n} \bullet \mathbf{B_{ext}} & = \left(-\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}\right) \bullet \sqrt{3} \left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right) \\ & = \sqrt{3} \left(-\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}\right) \bullet \left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right) \\ & = \sqrt{3} \Biggr[ \left(-\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}} \right) + \left(-\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}} \right) + \left(-\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}} \right) \Biggr] \\ & = \sqrt{3} \Biggr[ -\frac{1}{3} -\frac{1}{3} -\frac{1}{3} \Biggr] \\ & = \sqrt{3} \Bigr[- 1 \Bigr] \\ \mathbf{\hat n} \bullet \mathbf{B_{ext}} & = -\sqrt{3} \\ \end{align} }[/math]
We can now find the magnetic potential energy of the loop:
[math]\displaystyle{ U(\theta) = \sqrt{3} \times 5 \times \pi \times (2)^2 = 20 \sqrt{3} \pi \approx 108.83 \text{ J} }[/math]
Keep in mind we could have found the angle between [math]\displaystyle{ \mathbf{\hat n} }[/math] and [math]\displaystyle{ \mathbf{B_{ext}} }[/math] and used
[math]\displaystyle{ U(\theta) = - [\mu B_{ext}] \ \text{cos}(\theta) }[/math]
to find the magnetic potential energy. The angle found would be [math]\displaystyle{ \pm 180° }[/math], corresponding to an anti-parallel relation between the magnetic field and the magnetic moment, and therefore a max potential energy.

Difficult

A thin uniform ring of radius [math]\displaystyle{ R }[/math] and mass [math]\displaystyle{ M }[/math], carrying a uniformly distributed charge [math]\displaystyle{ +Q }[/math], rotates clockwise (as seen from above) about its axis with a constant angular speed [math]\displaystyle{ \omega }[/math]. It lies in the xy-plane.

a) Find the ratio of the magnitude of the ring's magnetic dipole moment [math]\displaystyle{ (\mu) }[/math] to its angular momentum [math]\displaystyle{ (L) }[/math].
The current in the ring can be calculated using the period of the rotation [math]\displaystyle{ (T) }[/math] and the charge on the ring as:
[math]\displaystyle{ I = \frac{dQ}{dt} = \frac{\Delta Q}{\Delta t} = \frac{Q}{T} = \frac{Q \omega}{2 \pi} }[/math]
The magnetic moment is:
[math]\displaystyle{ \mu = I A = \frac{Q \omega}{2 \pi} \cdot \pi R^2 = \frac{1}{2} QωR^2 }[/math]
The angular momentum is calculated as the loops rotational inertia (moment of inertia) times its angular speed. The rotational inertia of a ring is given by [math]\displaystyle{ m R^2 }[/math]:
[math]\displaystyle{ L = I \omega = m R^2 \omega }[/math]
Therefore, the ratio is:
[math]\displaystyle{ \frac{\mu}{L} = \frac{\frac{1}{2} Q \omega R^2}{m R^2 \omega} = \frac{Q}{2m} }[/math]
b) What is the torque experienced by the ring if an external magnetic field described by [math]\displaystyle{ \mathbf{B} = (2, 4, -5) }[/math] is applied to the ring?
We know the torque experienced by a current carrying loop is described by:
[math]\displaystyle{ \boldsymbol{\tau} = \boldsymbol{\mu} \times \mathbf{B} \ \mathbf{(1)} }[/math]
The magnitude of [math]\displaystyle{ \boldsymbol{\mu} }[/math] was found to be [math]\displaystyle{ \frac{1}{2} Q \omega R^2 }[/math] in the previous part. To find the direction of [math]\displaystyle{ \boldsymbol{\mu} }[/math], we consider the direction of the current and where the ring lies. Since the ring is lying in the xy-plane and rotating clockwise, using the right-hand rule shows [math]\displaystyle{ \boldsymbol{\mu} }[/math] must point in the [math]\displaystyle{ -z }[/math] direction. A unit vector in this direction can be described as [math]\displaystyle{ \mathbf{\hat n} = (0, 0, -1) }[/math].
Thus, [math]\displaystyle{ \boldsymbol{\mu} }[/math] can be described by:
[math]\displaystyle{ \boldsymbol{\mu} = \mu \mathbf{\hat n} }[/math]
Plugging this into 1 shows:
[math]\displaystyle{ \begin{align} \boldsymbol{\tau} & = \mu \bigr[ \mathbf{\hat n} \times \mathbf{B} \bigr] \\ & = \mu \bigr[(0, 0, -1) \times (2, 4, -5) \bigr] \\ & = \mu \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 0 & -1 \\ 2 & 4 & -5 \end{vmatrix} \\ & = \mu \biggr[ \ \mathbf{i} \begin{vmatrix} 0 & -1 \\ 4 & -5 \end{vmatrix} - \mathbf{j} \begin{vmatrix} 0 & -1 \\ 2 & -5 \end{vmatrix} + \mathbf{k} \begin{vmatrix} 0 & 0 \\ 2 & 4 \end{vmatrix} \biggr] \\ & = \mu \biggr[\mathbf{i} \bigr[(0) - (-4) \bigr] - \mathbf{j} \bigr[(0) - (-2) \bigr] + \mathbf{k} \bigr[(0) - (0) \bigr] \biggr] \\ & = \mu \bigr[4 \mathbf{i} - 2 \mathbf{j} + 0 \mathbf{k} \bigr] \\ & = \frac{1}{2} Q \omega R^2 \cdot (4, -2, 0) \\ & = Q \omega R^2 \cdot (2, -1, 0) \\ \boldsymbol{\tau} & = \sqrt{5} \cdot Q \omega R^2 \left(\frac{2}{\sqrt{5}}, -\frac{1}{\sqrt{5}}, 0 \right) \end{align} }[/math]

Connectedness

Insert Connectedness Section here

History

The study of magnetism dates far back in time, but it was not until 1825 that Andre Ampere showed that magnetism is due to perpetually flowing current through loops of wire. He then went on to derive Ampere's Law, which connected magnetic fields to electric currents. This equation was then further adapted to simplify the on axis magnetic field generated by a loop of current to use the magnetic dipole moment.

At first, people thought magnets, both natural and man-made, are made up of countless magnetic dipoles, each consisting of positive and negative magnetic charges separated by a small distance. This consequently defined the concept of magnetic dipole moment, a vector, pointing from the negative magnetic charge to the positive magnetic charge. When scientists discovered that magnetic charges, or "magnetic monopoles" do not exist, the magnetic properties of matter were believed to be generated by the alignment of molecular currents. Since then, magnetic dipole moment has been redefined using current [math]\displaystyle{ I }[/math], allowing the idea of magnetic dipole to remain.

See also

Here are some more resources with extra information on magnetic dipole moments.

Further reading

External links

References

This section contains the the references you used while writing this page

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Magnetic_Dipole_Moment&oldid=41126"