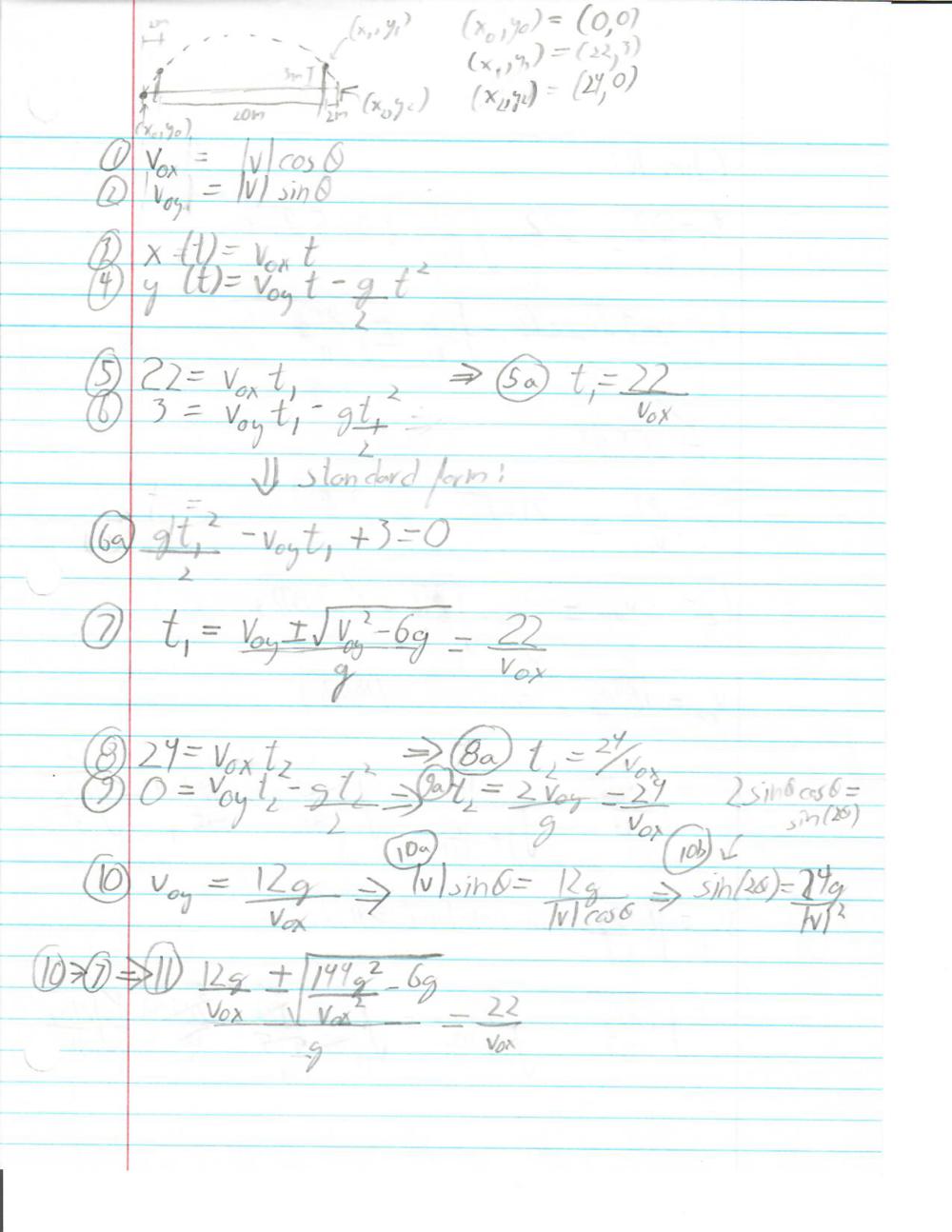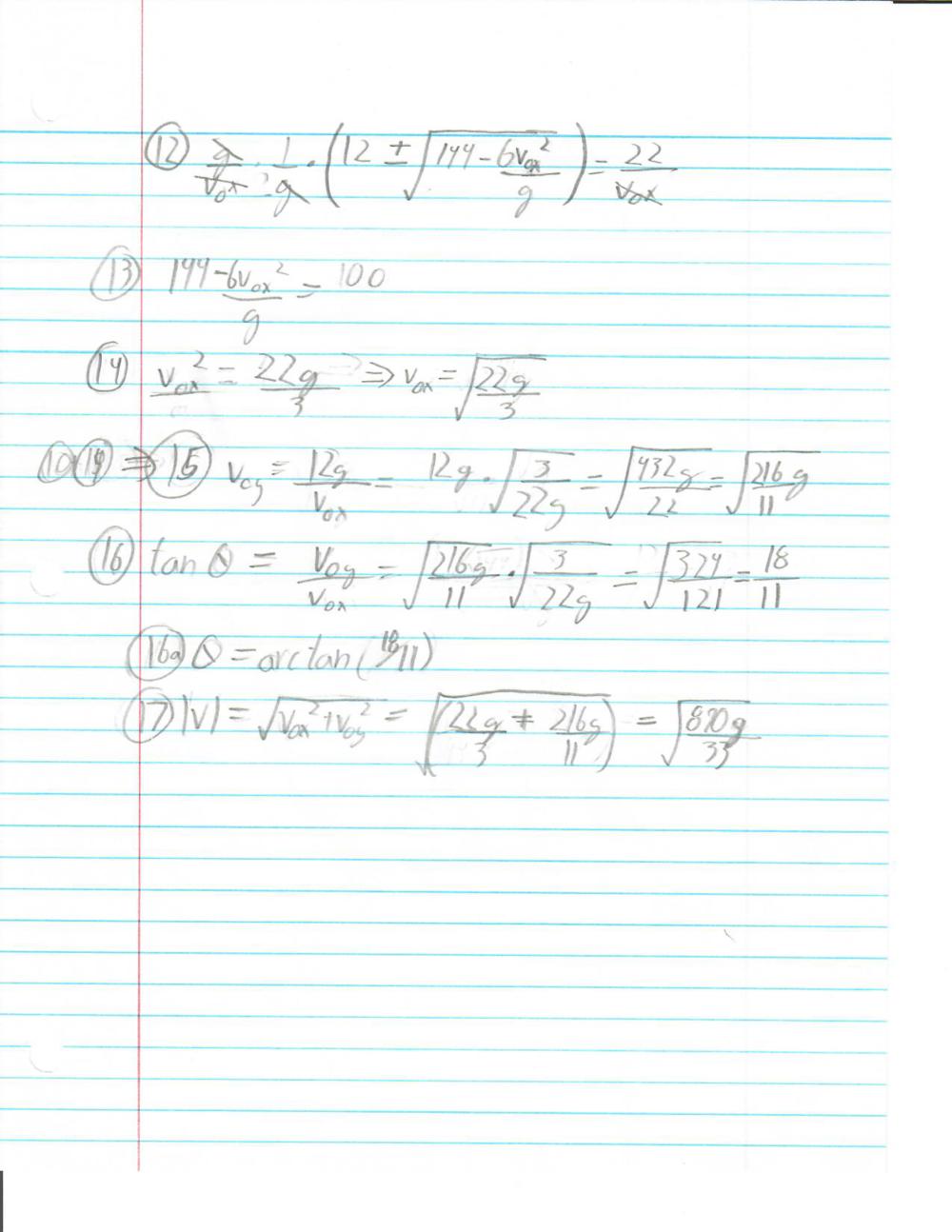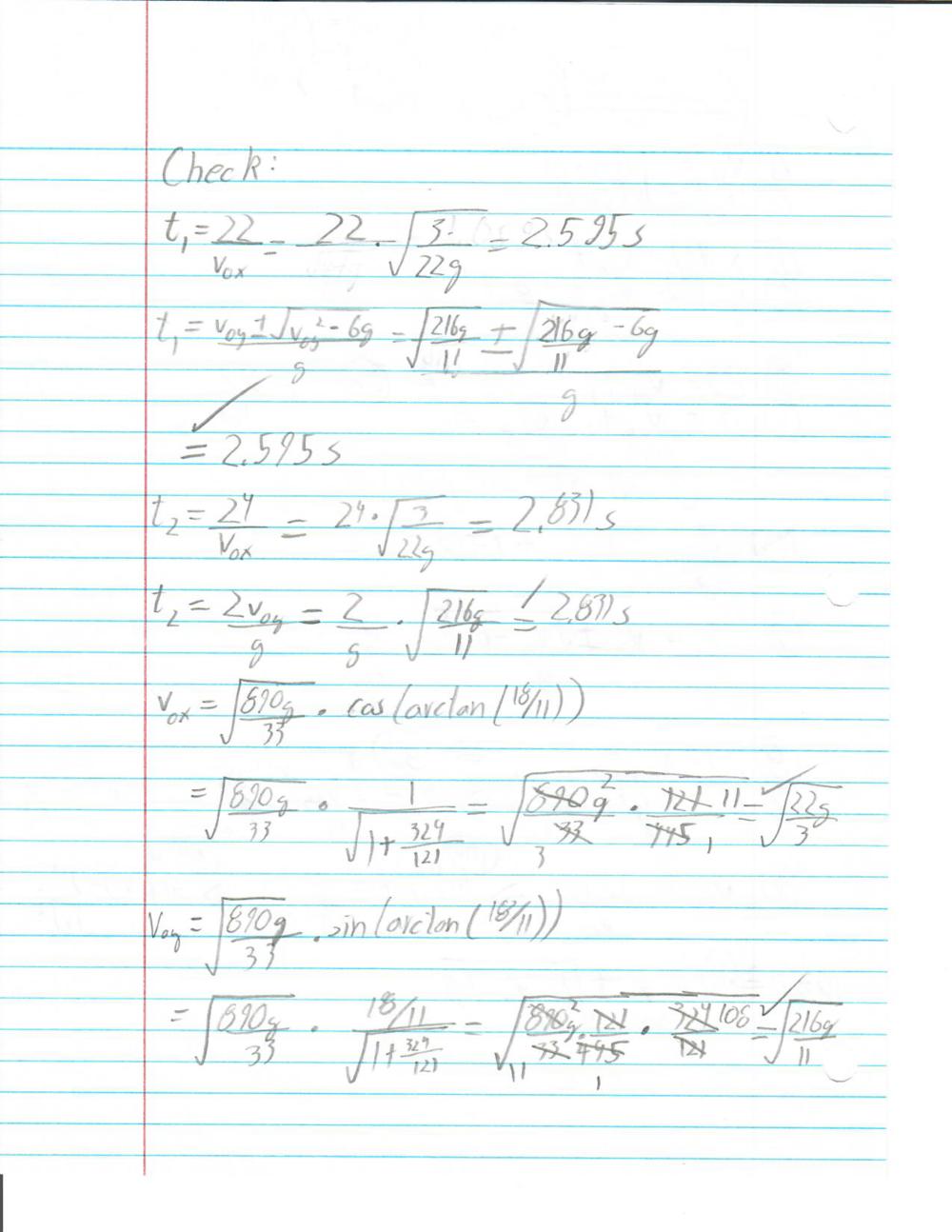Projectile Motion

Motion in which an object is affected only by the constant force of gravity is referred to as projectile motion (and the object as a projectile). This scenario is necessarily a simplification, since one larger scales gravity is not constant as one moves away from the attracting object, and there is also usually air resistance acting upon the object. However, it is a useful approximation, and an instructive use of kinematics.

The Main Idea

Projectile motion is a branch of classical mechanics which analyzes the motion of objects (projectiles) under the influence of the constant acceleration of gravity near the surface of the earth. Often, the projectiles are propelled prior to being analyzed under the influence of gravity, giving them initial velocities that affect their trajectories. Two classic examples of projectile motion are the firing of a cannon and throwing a ball off a tower. An object is a projectile if it is subject only to the constant force of gravity. For real projectiles, other forces such as air resistance are usually present, but these make the mathematical model significantly more complicated, and fair estimations may be gotten when disregarding them for many cases (note, however, that the relative importance of these forces increases for a feather vs for a ball). Regardless of the direction of motion of the projectile, the free-body diagram of a projectile is always the same, and constant throughout its trajectory: a particle on which only gravity acts in a downward direction.

A Mathematical Model

Traditionally, the Frame of Reference chosen for projectile motion problems places the origin on the ground below the point of launch and defines t=0 to be the time of launch.The +y direction is usually defined as vertically upwards, so the gravitational force acts in the -y direction. Because there will be no forces horizontal to the ground, it is possible to define our coordinate system with the +x direction as the direction of the horizontal component of the projectile's velocity, and in doing so ignore the third dimension altogether. The y component of the velocity is constantly changing over time due to the gravitational force. Gravity near the surface of the earth causes a constant downward acceleration of 9.8m/s^2. This causes a parabolic trajectory. The constant velocity in the x direction and the constant acceleration in the y direction lend themselves to the Kinematic Equations. Kinematics are used to analytically solve problems related to projectile motion.

The following equations derived from kinematics describe the x and y components of a projectile's position as functions of time.

[math]\displaystyle{ y(t) = - \frac{1}{2} g \cdot t^2 + v_{y, 0} \cdot t + y_i }[/math]

[math]\displaystyle{ x(t) = v_{x, 0} \cdot t }[/math]

It is evident from the above equations that the two components of a projectile's motion are independent; the particle's horizontal position has no effect on its vertical motion and vice versa.

[math]\displaystyle{ v_{y, 0} }[/math] and [math]\displaystyle{ v_{y, 0} }[/math] may each be positive, negative, or 0, depending on how the projectile was launched, resulting in a variety of trajectory shapes. Below are some possible trajectories of projectiles:

Note that all of these shapes are parabolic.

Sometimes, an initial speed and an initial angle (usually with respect to the horizontal) is given. In this case, [math]\displaystyle{ v_{y, 0} = v_0 \sin \theta_0 }[/math] and [math]\displaystyle{ v_{x, 0} = v_0 \cos \theta_0 }[/math].

Sometimes, rather than giving an initial velocity, a projectile motion problem will give the mass of the projectile as well as the magnitude, direction, and duration of the propelling force launching it. From this information, the relationship between Impulse and Momentum can be used to find the initial velocity of the projectile. In these situations, the propelling force is usually considered the only force acting on the object during the pre-trajectory impulse, because even if other forces are present, they are usually negligible compared to the propelling force.

At the highest point in a projectile's trajectory, the projectile's velocity is entirely horizontal; the vertical component is 0. This is because at that point in time, the vertical velocity has stopped being positive and is no longer carrying the projectile higher, but has not yet become negative and has therefore not begun lowering the projectile once more.

A Computational Model

One method used to visualize or predict a projectiles trajectory is to apply our mathematical model using computational programming. Computer models usually use Iterative Prediction rather than Kinematics to determine the path of the projectile. Here is an example of a program in vPython that simulates a projectile:

Simulation of Projectile

Click "view this program" on the top left corner to view the source code.

When working with algebraic solutions such as this one, one may also make use of analytic solution engines such as Mathematica or Maple. The same snippet of code describing projectile motion is used here and in Kinematics:

 (*First Cell*)
 (*Setup for a generic projectile motion problem*)
 launchspeed = 10
 launchangle = Pi/6
 vinit = launchspeed*{Cos[launchangle], Sin[launchangle], 0}
 launchpos = {0, 0, 0}
 yterminus = 0 
 g = 9.8

Naturally, one can edit these values to set up a different problem. The setup and the equation solution itself is separated into two cells (Mathematica has a cell notebook based structure) for cleanliness' sake.

 (*Second Cell*)
 (*Solving for the time of impact, then plugging that in to the original equations to find position in x and y *)
 T = Solve[-g*t^2/2 + vinit[[2]]*t + launchpos[[2]] == yterminus, t]
 finalpos = {(vinit[[1]]*t + launchpos[[1]]) /. T, (-g*t^2/2 + vinit[[2]]*t + launchpos[[2]]) /. T, 0}
 (* This gives 2 answers, the user must determine which is useful: if yinit  = 0, one will be at t=0, if yinit >0, one will be at t <0, if yinit < 0, both will be at t>0, so in the last case 
 you need to think about the situation*)

Examples

1. (Simple)

A ball leaves a table which is [math]\displaystyle{ 1.5 \; m }[/math] high with a horizontal velocity of [math]\displaystyle{ 2.5 \; \frac{m}{s} }[/math]. What is the duration of the flight, and what is the horizontal distance it will travel over this time?

Solution

2. (Middling)

A cannon fires a [math]\displaystyle{ 10 \; kg }[/math] projectile with [math]\displaystyle{ 20,000 \; N }[/math] of force over a duration of [math]\displaystyle{ 0.1 \; s }[/math]. The cannon may be fired at angles of [math]\displaystyle{ 30^\circ, 60^\circ, }[/math] and [math]\displaystyle{ 90^\circ }[/math]. What is the distance the projectile will follow at each of these angles? Which angle will lead to the furthest distance of travel?

Solution

In the example above, the time of flight of each cannonball is determined by finding the time until its highest point and doubling that. This is possible because for this problem the ground is flat; if the cannonball ends up higher or lower than it starts, the time of flight will have to be found using its y-coordinate as a function of time. Once the time of flight is found, it is multiplied by the x component of its velocity to find its horizontal displacement.

3. (Difficult)

The largest snowstorm in a century has come through Atlanta, and you and your friends have decided to have an extremely elaborate snowball fight. You each have constructed snow fort walls 3 meters high (there was a lot of snow), separated by a distance of 20 meters. Now you need to launch your snowball (from a spring loaded cannon, of course) in a perfect parabolic arc in order to hit a target on the ground, exactly two meters behind your friend's snow fort walls. Your cannon is, in turn, exactly two meters behind your wall. Neglecting air resistance, find the angle and launch speed which will allow you to just barely clear the wall, then hit the target on the ground (in other words, the trajectory will have two known points, one at the top point of the wall, and one at the target).

Solution

Since this problem is somewhat tricky, especially in the algebra, the original solution process is attached, along with the set of checks to ensure that the answer is correct.

4. (Bonus)

As a challenge, determine the angle at which the distance traveled will be maximized, and prove that this is the maximum. Hint: find the range of the projectile as a function of the launch angle, then use optimization (find the angle at which the derivative of this function with respect to angle is equal to zero).

Additional examples of projectile motion can be found on the Kinematics page.

Connectedness

[A student should expand upon this]

Projectile motion has many applications in day-to-day life; every dropped, thrown, and launched object massive enough to disregard air friction is an example of projectile motion.

Application: rifle scope industry

A bullet fired from a horizontal hunting rifle obeys the model of projectile motion, so by the time it reaches a given horizontal distance from the hunter, it will have fallen vertically by a predictable amount. The scope of a hunting rifle can be calibrated to specific distances. This angles the scope slightly below the horizontal to take into account the bullet drop; when the bullet reaches the horizontal distance of interest, it will have fallen exactly into the crosshair of the scope. The design and manufacture of the scopes and their calibration mechanisms require a quantitative understanding of projectile motion.

History

The history of projectile motion is closely entwined with the history of Kinematics, and so in many ways the history of one is the history of the other. A few special notes may be made about projectiles though. Aristotle was one of the first to write extensively about the motion of objects, and made a number of claims. First, he argued that heavy objects (like stones) fall because they are made primarily of earth, which is attracted to other earth, whereas smoke rises because it is made of air, and is attracted to other air. He also believed that objects move only due to propelling forces, leading him to conclude that the air itself pushes objects forward, through some form of vacuum interaction.

It was Galileo who recognized the flaws in this argument, and who instead put forth the idea of inertia, that objects will stay in motion unless acted upon by outside forces. Galileo also identified the parabolic arcs characteristic of projectile motion.

These developments were formalized and given greater detail by Newton, who explained them and many other phenomena through his laws and the development of appropriate mathematical techniques.

Several important figures have contributed to the modern understanding of projectile motion.

Aristotle

The first findings of Projectile Motion were contributed by Aristotle. He believed that a projectile modeled by a canon ball travels in a straight line until it lost its 'impetus'. When it lost its 'impetus' which ran out after time, due to a restive force, the projectile would immediately drop and fall to the ground. For objects projected over short distances, at first observation this can visually appear to be true.

Galileo

Galileo's findings were motivated by the Renaissance. Through as series of experiments, he discovered that projectile motion is a result of free fall motion along the y-axis and uniform (constant velocity) motion along x-axis. This model became well-known and led to new insights on projectile motion, such as its parabolic shape. It is still accepted today.

One experiment Galileo performed in developing this model consisted of dropping two objects from equal heights: one from rest, and one with an initial horizontal velocity. Both struck the ground at the same time because both had the same initial vertical velocity. The horizontal component of velocity does not affect its vertical motion because the components of motion are independent.

Isaac Newton

Isaac Newton contributed to the idea of projectile motion with his idea of a cannon on a mountaintop, now known as Newton's cannonball. Newton hypothesized that a cannon on top of a high mountain could fire a ball with varying initial speeds for varying trajectories. A cannonball simply dropped off the mountain would merely return to earth, but if that cannonball were fired from a cannon then it would return to Earth in an arc, or parabolic shape. This would be considered projectile motion. Neither of these scenarios were new or particularly innovative, but Newton also imagined a third scenario in which the cannonball were launched at great speed. In this scenario, he imagined that the ball would travel so far before curving downward that the earth would curve underneath it due to its spherical shape, resulting in a circular orbit. In doing so, Isaac Newton became one of the first to imagine universal gravity and to come up with a cause for orbital motion. It is worth noting that Newton's contribution does not strictly fall under the category of projectile motion as it is defined on this page because in the case of a cannonball orbiting the earth, gravity is not constant and downward, but changes its direction depending on the cannonball's position to point towards the center of the earth.

See also

Kinematics

Velocity

Acceleration

Iterative Prediction

External links

Interactive Projectile Simulator