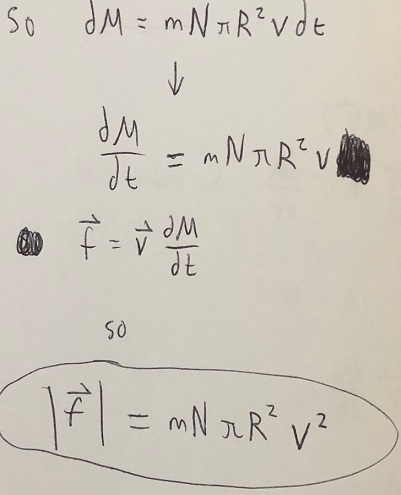Newton's Second Law: the Momentum Principle

This page describes Newton's second law, also known as the momentum principle, which relates net force to the change in linear momentum. This principle is used to predict the effects of forces on the motion of objects.

The Main Idea

Newton's second law, also known as the momentum principle, states that [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}_{system}}{dt} }[/math] where [math]\displaystyle{ \vec{p} }[/math] is the linear momentum of a system, [math]\displaystyle{ \vec{F}_{net} }[/math] is the net external force acting on the system from its surroundings, and t is time. Often, the system in question consists of a single particle whose motion we want to predict. Note that both force and momentum are vector quantities, and that the change in momentum as a result of a force will always be in the direction of that force.

The momentum principle has no derivation, as it is considered the definition of force.

A Mathematical Model

The momentum principle states that [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math]. Recall that [math]\displaystyle{ \vec{p} = m\vec{v} }[/math]. Therefore, by product rule, [math]\displaystyle{ \frac{d\vec{p}}{dt} = m\frac{d\vec{v}}{dt} + \vec{v}\frac{dm}{dt} }[/math]. Under the assumption that mass is constant, the second term becomes 0, and the momentum principle becomes [math]\displaystyle{ \vec{F}_{net} = m\frac{d\vec{v}}{dt} }[/math], or [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math], which may be a more familiar form of Newton's second law. The form [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] is preferred for several reasons:

1. When a particle accumulates mass that was initially at rest, such as a snowball rolling downhill, the term [math]\displaystyle{ \vec{v}\frac{dm}{dt} }[/math] is not 0, and [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] is no longer accurate, while [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] is;
2. As a particle approaches the speed of light, [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] is no longer accurate, while [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] is, as long as relativistic momentum is used; and
3. [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] has a more direct rotational analogue- that is, it will be easier to accurately learn rotational physics if you learn linear physics using this form.

That said, the relation [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] can often be of use when the particle is known to have a constant mass and travel at non-relativistic speeds, particularly in combination with kinematic equations that also use [math]\displaystyle{ \vec{a} }[/math] (see kinematics).

The momentum principle is responsible for the relationship between impulse and momentum.

Examples

1. (Simple)

At t=0, a 4kg particle is released from rest and a constant 12N force begins acting on it. How far way is the particle after 5 seconds?

For this problem, it is easier to use [math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] than [math]\displaystyle{ \vec{F}_{net} = \frac{d\vec{p}}{dt} }[/math] because it allows us to solve for [math]\displaystyle{ \vec{a} }[/math] which can then be used in a kinematic equation. We know this form of Newton's second law is accurate because the particle travels at non-relativistic speeds and is of constant mass.

[math]\displaystyle{ \vec{F}_{net} = m\vec{a} }[/math] can be rearranged into [math]\displaystyle{ \vec{a} = \frac{\vec{F}_{net}}{m} }[/math]

[math]\displaystyle{ a = \frac{12}{4} = 3 }[/math] (direction doesn't matter for this problem.)

[math]\displaystyle{ x_f = \frac{1}{2}at^2 + v_it + x_i = \frac{1}{2}(3)(5^2) = \frac{75}{2} }[/math]

2. (Intermediate)

A cylindrical rocket ship of mass [math]\displaystyle{ M }[/math] and speed [math]\displaystyle{ v }[/math] is cruising through outer space when it encounters a stationary dust cloud. The dust cloud has a number density of [math]\displaystyle{ N }[/math] particles per unit volume, and each dust particle has a mass of [math]\displaystyle{ m }[/math]. The rocket ship has a sticky surface on its front face that allows it to accumulate all of the dust that it hits, absorbing it into its mass. The radius of the rocket ship's circular face is [math]\displaystyle{ R }[/math]. What force does the rocket's thruster need to exert on it in order to preserve its speed as it moves through the dust cloud? (Assume that the consumption of fuel has a negligible impact on the mass of the rocket.)

Advanced Note: in order to use [math]\displaystyle{ \frac{dm}{dt} }[/math] for the accumulation of mass, the accumulated mass (i.e. the dust) must initially be at rest, like in the above problem. Otherwise, one must treat the accumulation of dust particles as a series of collisions, or change one's frame of reference so that the accumulated mass is initially at rest.

3. (Difficult)

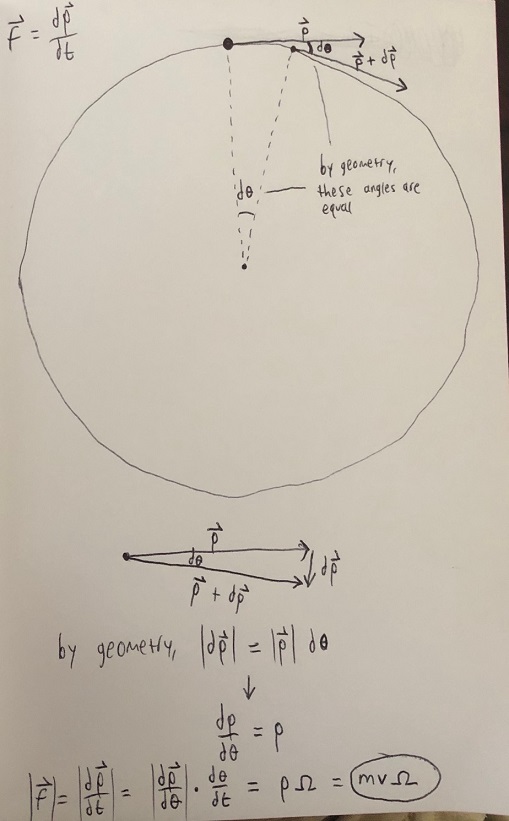
A particle of mass [math]\displaystyle{ m }[/math] and speed [math]\displaystyle{ v }[/math] moves in a circular path. Its angular frequency is [math]\displaystyle{ \Omega }[/math]. (Angular frequency is the rate at which the angle of the particle's position is changing in radians per unit time.) Using the momentum principle, show that

a) a nonzero net force is acting on the particle,

b) the magnitude of the force is given by [math]\displaystyle{ f = mv\Omega }[/math], and

c) the direction of the force is inwards towards the center of the circle.

a) The particle's momentum vector is changing over time; its magnitude is constant (mv), but its direction changes as its position along the circular path changes. It is always tangential to the circular path. Since [math]\displaystyle{ \vec{p} }[/math] changes over time, a nonzero net force must be acting on the particle. In fact, the only way a particle of constant mass can have a net force of 0 acting on it is if it is travelling along a straight line at a constant speed, or if it is at rest.

b)

c) As one can see from the diagram above, [math]\displaystyle{ d\vec{p} }[/math] is pointing towards the center of the circle. If the particle is exactly at the top of the circle, its momentum is to the right (or left if the particle is travelling counterclockwise), and as [math]\displaystyle{ d\theta }[/math] approaches 0, [math]\displaystyle{ d\vec{p} }[/math] approaches a downward direction, which is towards the center of the circle.

For more information, see Centripetal Force and Curving Motion. Our answer agrees with the formulas given on that page.

See also

External links

1. nhttp://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/Part_III/Chapter_3_Stress_Mass_Momentum/Stress_Balance_Principles_02_The_Momentum_Principles.pdf
2. http://acme.highpoint.edu/~atitus/phy221/lecture-notes/2-2-momentum-principle.pdf

References

• William, Harris. "How Newton's Laws of Motion Work" 29 July 2008. HowStuffWorks.com. <https://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion.htm> 11 April, 2018.
• http://www.physicsclassroom.com/class/newtlaws/Lesson-3/Newton-s-Second-Law