Centripetal Force and Curving Motion

Main Idea

Centripetal forces are everywhere in our daily lives, from when we drive a car to when a racer goes around a banked turn and beyond.

A centripetal force is a force acting on a body while it has a curving motion. In these certain situations, the momentum of the system is not constant, since the direction of motion or velocity always changes direction while the speed may remain constant. For example, imagine you are kicking a ball that is moving perpendicular to the direction of motion. Now if you keep kicking the ball in this similar manner for a small duration of time, the ball would move in a circular path (Chabay, Sherwood). In fact, a body cannot travel in a circle if there is no centripetal force.

It is important to note that a centrifugal force is equal and opposite to the centripetal force, however it is the apparent force that throws a body away from the centre of the circle, not the true force, that being the centripetal force.

When an object is moving in vertical centripetal motion, for example when a man is swinging on a rope, the force gravity [math]\displaystyle{ mg }[/math] must be accounted for as well as the tension force [math]\displaystyle{ F_t }[/math].

Mathematical Model

While an object is in circular motion, the centripetal force is always perpendicular to the velocity and momentum of the object, meaning that the object experiences a force towards the centre of the circle while it is moving. The simple mathematical model for centripetal force is normally [math]\displaystyle{ F_c = ma_c = \frac{m v^2}{r} }[/math] for any object moving in a circle, where [math]\displaystyle{ r }[/math] is the radius of the circle, [math]\displaystyle{ v }[/math] is the tangential speed, and [math]\displaystyle{ m }[/math] is the mass of the object in motion. However, since this is circular motion, many times the angular velocity ω in [math]\displaystyle{ \frac{rads}{s} }[/math] of the system moving is given.

In this case

[math]\displaystyle{ v = \omega r }[/math]

meaning

[math]\displaystyle{ F_c = {m\omega^2 r} }[/math]

However sometimes the period of rotation [math]\displaystyle{ T }[/math], in seconds, is given by

[math]\displaystyle{ T = \frac{2\pi}{\omega} \,. }[/math]

Thus, the equation becomes

[math]\displaystyle{ F = m r \left(\frac{2\pi}{T}\right)^2 }[/math]

However in many circumstances, it is helpful to split the centripetal force into parallel and perpendicular forces, or [math]\displaystyle{ F_{\parallel} }[/math] and [math]\displaystyle{ F_{\perp} }[/math] respectively.

This means

[math]\displaystyle{ F_c = F_{\parallel} + F_{\perp} }[/math]

Thus we can rewrite the momentum principle as follows

[math]\displaystyle{ Δp = (F_{\parallel} + F_{\perp})Δt }[/math]

Normally, [math]\displaystyle{ F_{\parallel} }[/math] dictates the velocity of the object, while [math]\displaystyle{ F_{\perp} }[/math] dictates the direction of motion.

Computational Model

A computational representation of centripetal force can be created using VPython.

We can find the initial position, momentum, and forces in VPython.

   while t <30000000:
   rate(100)
   scene.center=moon.pos/2
   scene.range=Earth.radius*60
   p_init=mag(pcraft)
   pcraft_i=pcraft+vector(0,0,0)                                             #craft initial momentum
   r=Earth.pos-craft.pos                                                         #craft initial position from Earth
   rM=moon.pos-craft.pos                                                     #craft initial position from Mon
   Fgrav=G*mEarth*mcraft/(mag(craft.pos-Earth.pos)**2)     #gravity from earth
   FgravM=G*mcraft*mmoon/(mag(craft.pos-moon.pos)**2)      #gravity from moon
   pcraft=pcraft+r/mag(r)*Fgrav*deltat+rM/mag(rM)*FgravM*deltat   #new momentum of the craft based on Earth and Moon

From this we can calculate the change in momentum and the new positions based on the forces.

   deltap=pcraft-pcraft_i      #calculates change in momentum
   Fnet=deltap/deltat          #calculates Fnet from Earth and Moon
   p_final=mag(pcraft)         
   Fnet_tangent=((p_final-p_init)/deltat)*norm(pcraft)     #calculates Fnet par.
   Fnet_tangent_arrow.pos=craft.pos
   Fnet_tangent_arrow.axis=Fnet_tangent*1000000
   Fnet_perp=Fnet-Fnet_tangent                                       #calculates Fnet perp
   Fnet_perp_arrow.pos=craft.pos
   Fnet_perp_arrow.axis=Fnet_perp*1000000
   vcraft=pcraft/mcraft                #calculates new velocity of the craft

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

The purple arrow represents the direction of force on a spacecraft orbiting earth. The yellow arrow represents the velocity of the spacecraft. The yellow line represents the motion of the craft.

Using this computational model, we can model the motion of a space craft by accounting for the forces of the moon and the Earth. This can be used to calculate the initial speed necessary to crash the space craft into the moon (cause why not?).

Examples

Problems taken from Textbook and WebAssign Resources

Simple

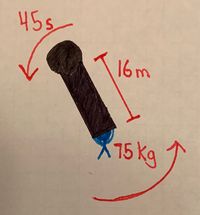
An engineer whose mass is 75 kg holds onto the outer rim of a rotating space station whose radius is 16 m and which takes 45 s to make one complete rotation.

a) What is the magnitude of the force the engineer has to exert in order to hold on?

Using our Mathematical Model, we can answer this in one step.

The force needed to hold on, or the centripetal force is:

[math]\displaystyle{ F_c = m r \left(\frac{2\pi}{T}\right)^2 = 75 \times 16 \left(\frac{2\pi}{45}\right)^2 = 23.39 \ \text{Newtons} }[/math]

Middling

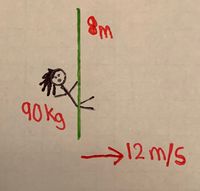
Tarzan, whose mass is 90 kg, is swinging on a vine. At the bottom most point, the 8 m long vine breaks. At that point he is traveling at 12 m/s.

a) What was the tension in the vine at the point it broke?

We know the centripetal force is what kept Tarzan in an arcing motion. This force must have been the difference between the tension in the vine and the downward pull of gravity (which in this case is all of the gravitational force):

[math]\displaystyle{ F_c = \frac{mv^2}{r} = F_T - mg }[/math]

Simplifying for tension gives:

[math]\displaystyle{ F_T = \frac{mv^2}{r} + mg }[/math]

Plugging in values gives:

[math]\displaystyle{ F_T = \frac{90 \times 12^2}{8} + 90 \times 9.81 }[/math]

Therefore:

[math]\displaystyle{ F_T = 2502.9 \ \text{Newtons} }[/math]

Difficult

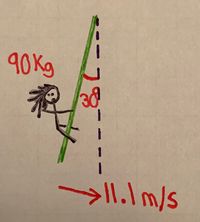
Tarzan, whose mass is 90 kg, is swinging on a vine. When the vine makes an angle of [math]\displaystyle{ \theta = 30^\text{o} }[/math] with the vertical, the 8 m long vine breaks. At that point he is traveling at [math]\displaystyle{ 11.1 \ \frac{m}{s} }[/math].

a) What was the tension in the vine at the point it broke?

We will follow the Middling example's strategy. We know the centripetal force will be the difference between the perpendicular forces, namely the perpendicular component of the gravitational force and the tension force:

[math]\displaystyle{ F_c = \frac{mv^2}{r} = F_T - F_{g_\perp} }[/math] (1)

The perpendicular component of the gravitational force can be found using right triangles. In the end, we find that:

[math]\displaystyle{ F_{g_\perp} = F_g \ \text{sin}(90 - \theta) = mg \ \text{sin}(60^\text{o}) }[/math]

Plugging this in to (1) gives:

[math]\displaystyle{ \frac{mv^2}{r} = F_T - mg \ \text{sin}(60^\text{o}) }[/math]

Simplifying for tension gives:

[math]\displaystyle{ F_T = \frac{mv^2}{r} + mg \ \text{sin}(60^\text{o}) }[/math]

Plugging in values gives:

[math]\displaystyle{ F_T = \frac{90 \times 11.1^2}{8} + 90 \times 9.81 \times \text{sin}(60^\text{o}) }[/math]

Therefore::

[math]\displaystyle{ F_T = 2150.7 \ \text{Newtons} }[/math]

Connectedness

How is this topic connected to something that you are interested in?

I really enjoy sitting in rollercoasters. Every time I visit any amusement park, that is my number one object, to ride as many rollercoasters as possible. I always feel strange forces on a rollercoaster. For example, I feel a sinking feeling every time I go through a dip and feel light when the car goes over a loop. These sensations are very strange, and sometimes you can feel them in a car as well. However, now I know that these are simply forces felt when the normal force is equal to the gravitational force.

How is it connected to your major?

In Aerospace Engineering, centripetal force always needs to be calculated to keep a body in orbit. This can define how fast a body is to be traveling and how heavy it should be to continue in orbit. It also defines how close to the planet it is to be. The force can also be used in the calculation gravity as a propelling force, by orbiting a planet to increase velocity.

Is there an interesting industrial application?

Applications of centripetal forces are used mostly in mechanical systems. For example, tire manufacturers need to know the amount of centripetal force that their tires need to be made to handle. This can influence how and of what material they make their tires. A centrifuge is also a device that uses centripetal force to separate materials, and are normally used in medical and chemical applications. A centrifuge is also an amusement park ride, that lets people stick to the wall while the centrifuge spins.

History

Sir Issac Newton discovered that the centripetal force is always towards the center of the circle using Kepler's Laws of Planetary Motion around the year 1666 in England. However, his perception of circular motion was incorrect, mainly since he thought it was caused by the balance of two forces, one centripetal, and the other centrifugal. Newton concluded that the centripetal force of any body must decrease as the inverse square of its distance from the center of its motion (Newton).

Centripetal Force and Curving Motion

Contents

Main Idea

Mathematical Model

Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu