Collisions: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
Line 1: Line 1:
Claimed by mdumenci3 for Fall 2017.
This entry covers collisions, the processes in which large interactions are
seen constrained in a short time period, with little interaction preceding and
succeeding the same period.


This topic covers Collisions, a comprehensive way to combine the Momentum and Energy Principles.
==Idea==
Collisions aren't special case events. They are commonly seen everywhere in our
daily lives: hopping a basketball, dropping our overly expensive phones and
car crashes being a few examples. As with everything we've learned so far,
collisions behave according to the fundamental principles. We're analyzing
them separately, because the nature of collisions allows us to make assumptions
that help us reason about these processes, and solve for unknowns.


==The Main Idea==
==Assumptions==
===Conserved momentum and energy===
If we take the colliding objects as the system, what assumption can we make
about the total momentum and energy of this system?


Collisions are special types of contact interactions between objects. From a physics standpoint, collisions are a way to combine the Momentum and Energy Principles. In the case of collisions, if we choose a system of the two objects interacting, the change in momentum of the system and the change in energy of the system are both zero. With this in mind, calculations with collisions become very simple. We are able to choose a system of only the two objects (excluding external forces such as the Earth's gravity) because the collision takes place during such a short time that the external forces have a negligible effect.
In our definition of a collision, we've said that interactions preceding
There are two types of collisions, [[Elastic Collisions]] and [[Inelastic Collisions]].  
and succeeding the process are tiny compared to the ones we see during the
process. The forces that contribute to this sudden spike of interactions is
internal to the system: they are between the colliding objects. Since we take
them as the system, we can make the assumption that the forces that act on the
system are negligible.


===A Mathematical Model===
By this assumption, the change in the total momentum and energy of the system
<math>{E}_{f} = {E}_{i}</math> where <math>{E}_{f}</math> is the total final energy of the system and <math>{E}_{i}</math> is the total initial energy of the system.
(of both the colliding objects) is negligible.


<math>{p}_{f} = {p}_{i}</math> where <math>{p}_{f}</math> is the total final momentum of the system and <math>{p}_{i}</math> is the total initial momentum of the system. (ie. <math>m_{f_1}v_{f_1} + m_{f_2}v_{f_2} + ... + m_{f_n}v_{f_n} = m_{i_1}v_{i_1} + m_{i_2}v_{i_2} + ... + m_{i_n}v_{i_n}</math>)
For <math>\Delta p = F * \Delta t</math>, <math>F</math> is negligible, thus
<math>\Delta p</math> is negligible.


===A Computational Model===
For <math>\Delta E = W_{surr} + Q</math>, <math>W_{surr} = F_{surr} * \Delta x</math>
The following situation was used for this model created using python:
and <math>Q = m * C * \Delta t</math>. <math>F_{surr}</math> and <math>\Delta t</math>
are negligible. Thus <math>\Delta E</math> is negligible.


Two objects are initially moving towards a third stationary object. Object 1 (in red) at position (-10,0,-2)m has a mass of 2kg and velocity (10,0,2)m/s. Object 2 (in blue) at position (0,6,3)m has a mass of 4kg and velocity (0,-6,3)m/s. Object 3 (in orange) at the origin has a mass of 5kg. The objects collide at the origin and after the collision it is observed that object 1 has embedded in object 3 (hence it is no longer visible in the model) and the combined object moves with velocity (5,-6,0)m/s (This is an example of a [[Maximally Inelastic Collision]]). The final velocity of object 2 is calculated and used in the rest of the simulation. (NOTE: the white sphere visible after the collision represents the origin to add dimension to the model and the delay during the collision is there to emphasis when and where the collision happens. Also use the link below the model for a more detailed explanation of the calculations and concepts.).
Therefore, we can assume that the total momentum and energy of the system
(of both the colliding objects) don't change during the collision.


[[File: CollisionsExample.gif]]
===Elasticity/Inelasticity and Kinetic Energy===
We can further characterize collisions by looking at the energy interactions
within the systems of collision.


Check out the code used for the simulation at [http://www.glowscript.org/#/user/samsaxlaxman/folder/Private/]. The code is commented pretty heavily (but it does assume some knowledge of python and python animations) in hopes that future students can modify some of the variables to experiment with creating different results.
In [[Elastic Collisions]], the total kinetic energy is conserved. None of the
kinetic energy of the system is transformed from or into <math>E_{internal}</math>,
such as thermal energy and spring potential energy.


==Examples==
An example for such a process is a Newton's Cradle, where the kinetic energy
of the colliding ball gets transformed into the kinetic energy of the last
ball in the cradle. The total kinetic energy is conserved.


Be sure to show all steps in your solution and include diagrams whenever possible
In [[Inelastic Collisions]], the total kinetic energy is not conserved. Some/all
of the kinetic energy of the system can be transformed from or into
<math>E_{internal}</math>.


===Simple===
An example for such a process is a car crash, where the kinetic energy of the
Example 1)
colliding car gets transformed into thermal energy and internal energy contained
A 0.5 kg soccer ball is moving with a speed of 5 m/s directly toward to 0.7 kg basket ball which is at rest.
in the crumbled, tense parts of the car chassis.
When two balls collide and stick together what will their final velocity be?


Before Collision: [[File: PhysicsWikiExample.png]]                                           After Collision: [[File: PhysicsWikiExampleb.png]]
([[Inelastic Collisions]] where there's maximum kinetic energy dissipation
are called [[Maximally Inelastic Collision]]. This doesn't necessarily mean
that _all_ of the kinetic energy gets transformed into <math>E_{internal}</math>,
since the total momentum is conserved, so there has to be some movement, thus
kinetic energy. Collisions where the objects stick together are
[[Maximally Inelastic Collision]].)


___
==Mathematical model==
By our assumptions, <math>p_f = p_i</math> and <math>E_f = E_i</math>
where subscripts <math>f</math> and <math>i</math> mean final and initial,
respectively.


Variables:
In an elastic collision, <math>K_{total, f} = K_{total, i}</math>.


<math>m_1 = 0.5</math> <math>kg</math>
In an inelastic collision, this equation doesn't hold, since
<math>\Delta E = \Delta K + \Delta E_{internal} = 0</math>, and
<math>\Delta E_{internal}</math> might be nonzero.


<math>v_{i_1} = 5</math> <math>m/s</math>
==Computational model==
In this model, two objects of different masses are moving towards each other
with equal magnitude, but opposite direction momenta.


<math>m_2 = 0.7</math> <math>kg</math>
The objects collide, and after the collision, it is observed that the objects
are embedded within each other with final velocity zero.


<math>v_{i_2} = 0</math> <math>m/s</math>
This is an example of a [[Maximally Inelastic Collision]]: none of the kinetic
energy is conserved.


<math>v_f = ?</math>
[https://trinket.io/glowscript/e600a7595e Computational Model]


Note: The behavior of the colliding objects are hardcoded in the model to
embed (vs. bouncing, etc.) This is an assumption we make about the
materials/internal structure of the balls. Correctly modeling deforming
objects without simplifying assumptions is a very complex task.


So, <math>m_1v_{i_1} + m_2v_{i_1} = (m_1 + m_2)v_f</math>


<math>LHS = (0.5</math> <math>kg)</math><math>(5</math> <math>m/s) +</math> <math>(0.7</math> <math>kg)</math><math>(0</math> <math>m/s) =</math> <math>2.5</math> <math>kg*m/s</math>
==Examples==


<math>RHS = (0.5</math> <math>kg +</math> <math>0.7</math> <math>kg)</math><math>(v_f) =</math> <math>(1.2</math> <math>kg)</math><math>(v_f)</math>
===Question 1===
A <math>0.5 kg</math> soccer ball is moving with a speed of <math>5 m/s</math>
directly towards a <math>0.7 kg</math> basket ball, which is at rest.


<math>LHS = RHS</math> in an inelastic collision
The two balls collide and stick together. What will be their final speed?


<math>2.5</math> <math>kg*m/s =</math> <math>(1.2</math> <math>kg)</math><math>(v_f)</math>
[[File:Collision-example-1-mert.png|500px]]


<math>v_f =</math> <math>(2.5</math> <math>kg*m/s)</math> <math>/</math> <math>(1.2</math> <math>kg) =</math> <math>2.08333</math> <math>m/s</math>
===Answer 1===
Let <math>m_1 = 0.5 kg</math>, <math>v_1 = 5 m/s</math>,
<math>m_2 = 0.7 kg</math>, <math>v_2 = 0 m/s</math>, where
subscripts <math>1</math> and <math>2</math> signify objects 1 and 2.


We're going to compute <math>v_f</math> for the collided mass.


Thus, the final velocity is 2.08 m/s. Since the two balls stick together, this is an example of a [[Maximally Inelastic Collision]].
We know that momentum is conserved. <math>p_f = p_i \implies p_f = p_1 + p_2
\implies p_f = (m_1 * v_1) + (m_2 * v_2)</math>.


===Middling===
We know that the objects stick together, hence their mass <math>m_1 + m_2</math>.
Example 2)
Then <math>p_f = (m_1 + m_2) * v_f \implies (m_1 + m_2) * v_f
A bullet of 50 caliber machine gun is 42 grams. It strikes a wooden target block of mass 10 kg stationed on a friction-less surface. The wooden block gains velocity of 1.8 m/s after being embedded with the bullet.
= (m_1 * v_1) + (m_2 * v_2)</math>.
What was the velocity of the bullet before it collided with the target?


Before Collision: [[File: PhysicsWikiExample2.png]]                                    After Collision: [[File: PhysicsWikiExample2b.png]]
If we solve for <math>v_f</math>, we get


----
<math>
\begin{aligned}
    v_f &= \frac{(m_1 * v_1) + (m_2 * v_2)}{m_1 + m_2} \\
        &= \frac{(0.5 * 5) +(0.7 * 0)}{0.5 + 0.7} \\
        &= 2.083 m/s
\end{aligned}
</math>


Variables:
This is a [[Maximally Inelastic Collision]], as the collided objects stuck
together. <math>K_{tot, f} < K_{tot, i}</math>.


<math>m_1 = 42</math> <math>g</math> <math>/</math> <math>1000</math> <math>g = </math><math>0.042</math> <math>kg</math>
-----


<math>v_{i_1} = ?</math>
===Question 2===
A <math>10 kg</math> asteroid with a velocity of <math><10, 0, 0> m/s</math>
crashes into the Earth in the Sahara Desert and bounces back into the space with
the same speed and opposite direction.


<math>m_2 =</math> <math>10</math> <math>kg</math>
Nobody is hurt, but some say that they felt the Earth recoil during
this unusual collision. Find the recoil velocity of the earth to see if it was
significant enough for people to have felt it. (Keep in mind that the human
sensory facilities aren't very precise.)


<math>v_{i_2} =</math> <math>0</math> <math>m/s</math>
[[File:Collision-example-2-mert.png|500px]]


<math>m_{1+2} = (m_1+m_2) = 0.042</math> <math>kg +</math> <math>10.0</math> <math>kg =</math> <math>10.042</math> <math>kg</math>
===Answer 2===
Let <math>m_a = 10 kg</math>, <math>m_e = 6 * 10^{24} kg</math>,
<math>v_{a, i} = <10, 0, 0> m/s</math>, <math>v_{a, f} = <-10, 0, 0> m/s</math>,
and <math>v_{e, i} = <0, 0, 0> m/s</math>, where subscripts <math>a</math>
and <math>e</math> signify the asteroid and the earth respectively.


<math>v_f =</math> <math>1.8</math> <math>m/s</math>
We're going to compute <math>v_{e, f}</math>


We know that momentum is conserved.


<math>(m_1)(v_{i_1}) + (m_2)(v_{i_2}) = (m_{1+2})(v_f)</math>
<math>
\begin{aligned}
    &p_f = p_i \\
    \implies &p_{a, f} + p_{e, f} = p_{a, i} + p_{e, i} \\
    \implies &(m_a * v_{a, f}) + (m_e * v_{e, f})
    = (m_a * v_{a, i}) + (m_e * v_{e, i})
\end{aligned}
</math>


<math>(0.042</math> <math>kg)(v_{i_1}) =</math> <math>(10.042</math> <math>kg)(1.8</math> <math>m/s)</math>
Solving for <math>v_{e, f}</math>, we get


<math>v_{i_1} = (18.0756</math> <math>kg*m/s)</math> <math>/</math> <math>(0.042</math> <math>kg) =</math> <math>430.37</math> <math>m/s</math>
<math>
\begin{aligned}
    v_{e, f}
        &= \frac{(m_a * v_{a, i}) + (m_e * v_{e, i}) - (m_a * v_{a, f})}{m_e} \\
        &= \frac{(10 * <10, 0, 0>) + (6 * 10^{24} * <0, 0, 0>)
            - (10 * <-10, 0, 0>)}{6 * 10^{24}} \\
        &= \frac{<100, 0, 0> + <100, 0, 0>}{6 * 10^{24}} \\
        &= <3.33 * 10^{-23}, 0, 0> m/s
\end{aligned}
</math>


The recoil velocity of the earth is too small for anyone to feel it--turns out
if humans want to believe in something, they will sometimes ignore facts and
do it anyway.


Final Answer: The bullet's initial speed is 430.37 m/s.
-----


===Difficult===
===Question 3===
Example 3) Two rocks in space are approaching a third stationary rock. Rock 1 has mass 30kg moves with velocity (13,-10,-2)m/s. Rock 2 has mass 60kg and moves with velocity (-3,23,3)m/s. Rock 3 has mass 35kg and is stationary. The rocks collide at rock 3's location. After the collision it is observed that Rock 1 has embedded into Rock 3, but a chunk of mass 15kg has broken off of the combined rock, Rock 3'. It is also noticed that Rock 2 is now moving with velocity (-2,12,2)m/s. (NOTE: due to the difficulty and use of three dimensions it is suggested to use a computer to solve this problem. Therefore the sample solution will involve code, but conceptually everything remains the same. Additionally some code is omitted for the sake of saving space, but the important calculations are included. See the entire code at [http://www.glowscript.org/#/user/samsaxlaxman/folder/Private/] with a model of the collision )
Two rocks in space are approaching a third, stationary rock. Rock 1 has a mass
of <math>30 kg</math> and moves with a velocity <math><13, -10, -2> m/s</math>.
Rock 2 has a mass of <math>60 kg</math>, and moves with a velocity
<math><-3, 23, 3> m/s</math>. Rock 3 has a mass of <math>35 kg</math>
and is stationary. The rocks collide at Rock 3's location.


'''First determine the momentum of Rock 3' plus the momentum of the 15kg chunk.'''
[[File:Collision-example-3a-mert.png|500px]]


<code>
After the collision, it is observed that Rock 1 has embedded
Having defined the rocks as o1, o2, and o3 respectively, and defined there initial masses and velocities to calculate their individual momenta
into Rock 3, which is now moving with a new velocity of <math><3, 5, 2> m/s</math>,
and that a chunk of mass <math>15 kg</math> has broken off of the combined rock.


calculated the total momentum of the system by adding
Rock 2, in the meantime, has a new velocity of <math><-2, 12, 2> m/s</math>.


totalP = o1.p+o2.p+o3.p #total momentum of the system
[[File:Collision-example-3b-mert.png|500px]]


Next update the o1, o2 and o3 objects with the information observed after the collosions
What is the change in the internal energy <math>\Delta E_{internal}</math> in
the system as a result of this three-way collision?


mChunk = 15 # in kg
===Answer 3===
Due to the complexity of this question, we are going to use a computer to
solve this problem. Conceptually, everything remains the same, but instead of
computing things by hand, we're getting help from a computer. Feel free to
solve it by hand if you want to!


m1f = 0 #final mass object 1 in kg
    # Define the initial masses/velocities of the rocks.
    mass_1_i = 30
    mass_2_i = 60
    mass_3_i = 35
   
    v_1_i = vector(13, -10, -2)
    v_2_i = vector(-3, 23, 3)
    v_3_i = vector(0, 0, 0)
   
    # Calculate the initial total momentum.
    total_p_i = (mass_1_i * v_1_i) + (mass_2_i * v_2_i) + (mass_3_i * v_3_i)
   
    # Calculate the masses/velocities of the rocks after the collision.
    mass_chunk = 15
   
    mass_2_f = 60
    mass_3_f = mass_1_i + mass_3_i - mass_chunk
   
    v_2_f = vector(-2, 13, 2)
    v_3_f = vector(3, 5, 2)
   
    # Calculate the velocity of the chunk. Remember that the momentum is conserved.
    v_chunk = (total_p_i - ((v_2_f * mass_2_f) + (v_3_f * mass_3_f))) / mass_chunk
   
    # Calculate the initial total kinetic energy.
    def kinetic_energy(mass, velocity):
        return 1/2 * mass * magnitude(velocity) ** 2
    k_tot_i = kinetic_energy(mass_1_i, v_1_i) \
            + kinetic_energy(mass_2_i, v_2_i) \
            + kinetic_energy(mass_3_i, v_3_i)
   
    # Calculate the final total kinetic energy.
    k_tot_f = kinetic_energy(mass_2_f, v_2_f) \
            + kinetic_energy(mass_3_f, v_3_f) \
            + kinetic_energy(mass_chunk, v_chunk)
   
    # Calculate the change in internal energy.
    d_e_internal = k_tot_f - k_tot_i


m2f = 60 #final  mass object 2 in kg
This Python snippet, when evaluated, will show that
<math>\Delta E_{internal} = 5175 J</math>.


v2f = vector(-2,12,2) #final  elocity object 2 in m/s
==Connectedness==
 
As we mentioned in the introduction to this article, collisions are everywhere
m3f = o1.m + o2.m - mChunk #final mass object 3 in kg
in our daily lives. Some examples are a bat colliding with a baseball in your
 
neighbor's backyard, two cars crashing in the highway in front of you, and so
create a new sphere object with mass 15kg (code omitted)
on.
 
calculate the final momentum of rock 2
 
o2.p = o2.v*o2.m
 
finally determine the combined momentum of rock 3' and the chunk using the momentum principle
 
pOfRock3PrimeAndChunk = totalP - o2.p #for now we are only calculating the combined momentum of rock 3' and the chunk
</code>
 
''The combined momentum of Rock 3' and the Chunk is <330, 360, 0>kg*m/s''
 
'''Later Rock 3' is observed moving with velocity (3,5,2)m/s, what is the velocity of the 15kg chunk?'''
 
<code>
Now we know the momentum of Rock 3' plus the chunk, AND we know the velocity and mass of Rock 3'
 
pRock3Prime = m3f*vector(3,5,2) #calculate the momentum of Rock3'
 
pChunk = pOfRock3PrimeAndChunk - pRock3Prime #calculate the momentum of the chunk
 
chunk.v = pChunk/chunk.m #calculate the final velocity of the chunk
</code>
 
''The velocity of the chunk is <7, -1, -10>''
 
'''With the information you know, determine the combined change in internal energy for all of the rocks.'''
 
<code>
Start by calculating the total Kinetic Energy initial and the total Kinetic Energy final (In the actual program this has to go above the update statements for after the collision)


<math>o1.K = .5*o1.m*o1.v**2</math>
Depending on the nature of the collision we can usually guess whether it's
an [[Elastic Collision]] or an [[Inelastic Collision]], and reason about it.
(If it's a car crash, things crumble, so there's increase in thermal energy, etc.)


o2.K= .5*oK.m*o1.v**2
Another very interesting application of collisions is in the field of astronomy.
The universe is ever-changing and we never know what might come our way.
A large meteor could be flying at the Earth with a very high speed and we could
use our knowledge of collisions to find out how the Earth will move after the
collision, what the temperature change of the area would be, and how the rest
of the Earth would be effected by the collision. By using our collision skills,
we could evacuate anyone who is prone to harm during the collision.


o3.K = 0 #because it is stationary
Since collisions are ubiquitous processes, knowledge about them is instrumental
 
for any engineer who deals with the physical world.
kTotInitial = o1.K+o2.K
 
Now after the collision (in the actual program these go after the update statements for after the collision)
 
o2.K = .5*o2.m*o2.v**2
 
kRock3Prime = .5*m3f*mag(vector(3,5,2))**2
 
chunk.K = .5*chunk.m*chunk.v**2
 
kTotFinal = o2.K + kRock3Prime + chunk.K
 
Now since there aren't any outside forces doing work and contributing energy, we know that change in internal energy equals -1*change in Kinetic energy, or kTotInitial - kTotFinal
 
changeInInternalEnergy = kTotInitial - kTotFinal
</code>
 
''The change in internal energy is 5175J''
 
==Connectedness==
Collisions are interesting phenomenons that are applicable to everyday situations. Some examples are when a bat collides with a baseball in your neighbor's backyard, two cars crashing in the highway in front of you, and two linebackers running into each-other at your local College's spring football game. Depending on the type of collision, you can predict if there will be a change in internal energy (thermal energy, chemical energy etc.). Another very interesting application of collisions is in the field of astronomy. The universe is ever-changing and we never know what might come our way. A large meteor could be flying at the Earth with a very high speed and we could use our knowledge of collisions to find out how the Earth will move after the collision, what the temperature change of the area would be, and how the rest of the Earth would be effected by the collision. By using our collision skills, we could evacuate anyone who is prone to harm during the collision.
 
Knowledge of collisions is also a must for many engineering majors. Industrial engineers must take in collisions when they are trying to optimize complex systems. For instance, an Industrial engineer must make sure that the bridge he or she builds can withstand the forces the cars can exert on it. Architects and Civil engineers must design houses in a certain way so that slight collisions with other objects won't completely knock the house down. And of course, Mechanical engineers and Aerospace engineers must take into account collisions when designing and maintaining mechanical systems.


==History==
==History==
In 1661, Christiaan Huygens, a Dutch physicist, concluded that when a moving body struck a stationary object of equal mass, the initial moving body would lose all of its momentum while the second object would pick up the same amount of velocity that the moving body had before the collision. He also stated that the total "quantity of motion" should be the same before and after the collision. This was the first thought of the conservation of momentum.
We've mentioned that collisions are not special case events in Physics--
 
the fundamental principles apply fully for them, and we reason about them
In 1687, Sir Isaac Newtons went a little further and stated in his third law of motion that the forces of action and reaction between two bodies are opposite and equal.  
using these principles. Then it won't surprise us that the history of collisions
 
is tangled with the history of the fundamental principles.
In Rutherford's Gold Foil Experiment in 1899, Rutherford found out that the plum pudding model of the atom was inaccurate and that there was actually a massive center of atoms. He did this through investigating atomic collisions between atoms and gold foil. Because some particles were scattered through angles larger than 90 degrees during the collisions, he was able to conclude that the atom had most of it's mass concentrated in a dense center rather than spread out evenly throughout the atom.
 
== See also ==


[[Maximally Inelastic Collision]] , [[Inelastic Collisions]] , [[Elastic Collisions]], [[Momentum Principle]], [[Net Force]].
In 1661, Christiaan Huygens, a Dutch physicist, concluded that when a moving
body struck a stationary object of equal mass, the initial moving body would
lose all of its momentum while the second object would pick up the same amount
of velocity that the moving body had before the collision. He also stated that
the total "quantity of motion" should be the same before and after the
collision. This was the first thought of the conservation of momentum.


===Further reading===
In 1687, Sir Isaac Newton went a little further and stated in his third law of
motion that the forces of action and reaction between two bodies are opposite
and equal. Because of this law; the total momentum of a closed system is constant.
Every force in the system has a reciprocal pair with an opposing direction, which
implies that their momentas cancel out, keeping the total momentum constant.


Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. 4th ed. Vol. 1. Hoboken, NJ: Wiley, 2015. Print. Matter and Interactions.
In Ernest Rutherford's famous Gold Foil Experiment of 1899, he found out that the plum
pudding model of the atom was inaccurate, and that there was a concentrated
core at the center of the atom (nucleus) and a lot of empty space around.
He didn't have access to the sophisticated tools/knowledge that we have now to
assist in his discovery: he did this through investigating atomic collisions
between alpha particles and gold foil. He shot alpha particles to a piece of
thin gold foil, and observed that some of the particles were scattered
through angles larger than 90 degrees during the collisions. Using collisions
principles, he was then able to reason that the atom had most of its mass
concentrated in a dense core, rather than spread out evenly throughout the atom
as the plum pudding model suggested.


Ehrhardt, H., and L. A. Morgan. Electron Collisions with Molecules, Clusters, and Surfaces. New York: Plenum, 1994. Print.
==See also==
[[Maximally Inelastic Collision]], [[Inelastic Collisions]],
[[Elastic Collisions]], [[Momentum Principle]], [[Energy Principle]],
[[Kinetic Energy]], [[Net Force]].


===External links===
==Further reading==
"The Collision Theory - Boundless Open Textbook." Boundless. N.p., n.d. Web. 17 Apr. 2016.
Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. 4th ed. Vol. 1.
Hoboken, NJ: Wiley, 2015. Print. Matter and Interactions.


"Momentum and Collisions – Background Material." Momentum and Collisions. School of Physics Sydney, Australia, n.d. Web. 17 Apr. 2016.
Ehrhardt, H., and L. A. Morgan. Electron Collisions with Molecules, Clusters,
and Surfaces. New York: Plenum, 1994. Print.


==References==
==References==
Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. 4th ed. Vol. 1.
Hoboken, NJ: Wiley, 2015. Print. Matter and Interactions.


Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. 4th ed. Vol. 1. Hoboken, NJ: Wiley, 2015. Print. Matter and Interactions.
"The Gold Foil Experiment." The Gold Foil Experiment. N.p., n.d. Web. 17 Apr.
 
2016.
"The Gold Foil Experiment." The Gold Foil Experiment. N.p., n.d. Web. 17 Apr. 2016.

Revision as of 18:21, 27 November 2017

This entry covers collisions, the processes in which large interactions are seen constrained in a short time period, with little interaction preceding and succeeding the same period.

Idea

Collisions aren't special case events. They are commonly seen everywhere in our daily lives: hopping a basketball, dropping our overly expensive phones and car crashes being a few examples. As with everything we've learned so far, collisions behave according to the fundamental principles. We're analyzing them separately, because the nature of collisions allows us to make assumptions that help us reason about these processes, and solve for unknowns.

Assumptions

Conserved momentum and energy

If we take the colliding objects as the system, what assumption can we make about the total momentum and energy of this system?

In our definition of a collision, we've said that interactions preceding and succeeding the process are tiny compared to the ones we see during the process. The forces that contribute to this sudden spike of interactions is internal to the system: they are between the colliding objects. Since we take them as the system, we can make the assumption that the forces that act on the system are negligible.

By this assumption, the change in the total momentum and energy of the system (of both the colliding objects) is negligible.

For [math]\displaystyle{ \Delta p = F * \Delta t }[/math], [math]\displaystyle{ F }[/math] is negligible, thus [math]\displaystyle{ \Delta p }[/math] is negligible.

For [math]\displaystyle{ \Delta E = W_{surr} + Q }[/math], [math]\displaystyle{ W_{surr} = F_{surr} * \Delta x }[/math] and [math]\displaystyle{ Q = m * C * \Delta t }[/math]. [math]\displaystyle{ F_{surr} }[/math] and [math]\displaystyle{ \Delta t }[/math] are negligible. Thus [math]\displaystyle{ \Delta E }[/math] is negligible.

Therefore, we can assume that the total momentum and energy of the system (of both the colliding objects) don't change during the collision.

Elasticity/Inelasticity and Kinetic Energy

We can further characterize collisions by looking at the energy interactions within the systems of collision.

In Elastic Collisions, the total kinetic energy is conserved. None of the kinetic energy of the system is transformed from or into [math]\displaystyle{ E_{internal} }[/math], such as thermal energy and spring potential energy.

An example for such a process is a Newton's Cradle, where the kinetic energy of the colliding ball gets transformed into the kinetic energy of the last ball in the cradle. The total kinetic energy is conserved.

In Inelastic Collisions, the total kinetic energy is not conserved. Some/all of the kinetic energy of the system can be transformed from or into [math]\displaystyle{ E_{internal} }[/math].

An example for such a process is a car crash, where the kinetic energy of the colliding car gets transformed into thermal energy and internal energy contained in the crumbled, tense parts of the car chassis.

(Inelastic Collisions where there's maximum kinetic energy dissipation are called Maximally Inelastic Collision. This doesn't necessarily mean that _all_ of the kinetic energy gets transformed into [math]\displaystyle{ E_{internal} }[/math], since the total momentum is conserved, so there has to be some movement, thus kinetic energy. Collisions where the objects stick together are Maximally Inelastic Collision.)

Mathematical model

By our assumptions, [math]\displaystyle{ p_f = p_i }[/math] and [math]\displaystyle{ E_f = E_i }[/math] where subscripts [math]\displaystyle{ f }[/math] and [math]\displaystyle{ i }[/math] mean final and initial, respectively.

In an elastic collision, [math]\displaystyle{ K_{total, f} = K_{total, i} }[/math].

In an inelastic collision, this equation doesn't hold, since [math]\displaystyle{ \Delta E = \Delta K + \Delta E_{internal} = 0 }[/math], and [math]\displaystyle{ \Delta E_{internal} }[/math] might be nonzero.

Computational model

In this model, two objects of different masses are moving towards each other with equal magnitude, but opposite direction momenta.

The objects collide, and after the collision, it is observed that the objects are embedded within each other with final velocity zero.

This is an example of a Maximally Inelastic Collision: none of the kinetic energy is conserved.

Computational Model

Note: The behavior of the colliding objects are hardcoded in the model to embed (vs. bouncing, etc.) This is an assumption we make about the materials/internal structure of the balls. Correctly modeling deforming objects without simplifying assumptions is a very complex task.


Examples

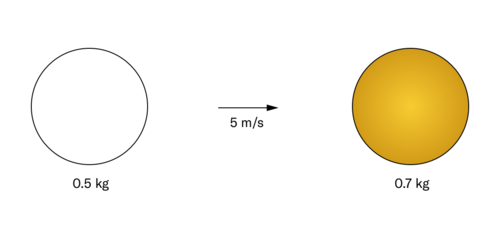
Question 1

A [math]\displaystyle{ 0.5 kg }[/math] soccer ball is moving with a speed of [math]\displaystyle{ 5 m/s }[/math] directly towards a [math]\displaystyle{ 0.7 kg }[/math] basket ball, which is at rest.

The two balls collide and stick together. What will be their final speed?

Answer 1

Let [math]\displaystyle{ m_1 = 0.5 kg }[/math], [math]\displaystyle{ v_1 = 5 m/s }[/math], [math]\displaystyle{ m_2 = 0.7 kg }[/math], [math]\displaystyle{ v_2 = 0 m/s }[/math], where subscripts [math]\displaystyle{ 1 }[/math] and [math]\displaystyle{ 2 }[/math] signify objects 1 and 2.

We're going to compute [math]\displaystyle{ v_f }[/math] for the collided mass.

We know that momentum is conserved. [math]\displaystyle{ p_f = p_i \implies p_f = p_1 + p_2 \implies p_f = (m_1 * v_1) + (m_2 * v_2) }[/math].

We know that the objects stick together, hence their mass [math]\displaystyle{ m_1 + m_2 }[/math]. Then [math]\displaystyle{ p_f = (m_1 + m_2) * v_f \implies (m_1 + m_2) * v_f = (m_1 * v_1) + (m_2 * v_2) }[/math].

If we solve for [math]\displaystyle{ v_f }[/math], we get

[math]\displaystyle{ \begin{aligned} v_f &= \frac{(m_1 * v_1) + (m_2 * v_2)}{m_1 + m_2} \\ &= \frac{(0.5 * 5) +(0.7 * 0)}{0.5 + 0.7} \\ &= 2.083 m/s \end{aligned} }[/math]

This is a Maximally Inelastic Collision, as the collided objects stuck together. [math]\displaystyle{ K_{tot, f} \lt K_{tot, i} }[/math].

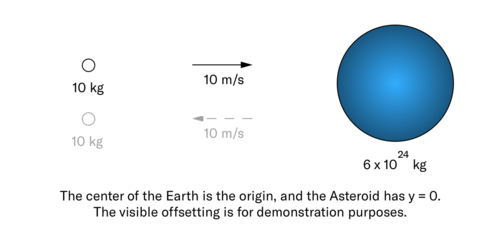
Question 2

A [math]\displaystyle{ 10 kg }[/math] asteroid with a velocity of [math]\displaystyle{ \lt 10, 0, 0\gt m/s }[/math] crashes into the Earth in the Sahara Desert and bounces back into the space with the same speed and opposite direction.

Nobody is hurt, but some say that they felt the Earth recoil during this unusual collision. Find the recoil velocity of the earth to see if it was significant enough for people to have felt it. (Keep in mind that the human sensory facilities aren't very precise.)

Answer 2

Let [math]\displaystyle{ m_a = 10 kg }[/math], [math]\displaystyle{ m_e = 6 * 10^{24} kg }[/math], [math]\displaystyle{ v_{a, i} = \lt 10, 0, 0\gt m/s }[/math], [math]\displaystyle{ v_{a, f} = \lt -10, 0, 0\gt m/s }[/math], and [math]\displaystyle{ v_{e, i} = \lt 0, 0, 0\gt m/s }[/math], where subscripts [math]\displaystyle{ a }[/math] and [math]\displaystyle{ e }[/math] signify the asteroid and the earth respectively.

We're going to compute [math]\displaystyle{ v_{e, f} }[/math]

We know that momentum is conserved.

[math]\displaystyle{ \begin{aligned} &p_f = p_i \\ \implies &p_{a, f} + p_{e, f} = p_{a, i} + p_{e, i} \\ \implies &(m_a * v_{a, f}) + (m_e * v_{e, f}) = (m_a * v_{a, i}) + (m_e * v_{e, i}) \end{aligned} }[/math]

Solving for [math]\displaystyle{ v_{e, f} }[/math], we get

[math]\displaystyle{ \begin{aligned} v_{e, f} &= \frac{(m_a * v_{a, i}) + (m_e * v_{e, i}) - (m_a * v_{a, f})}{m_e} \\ &= \frac{(10 * \lt 10, 0, 0\gt ) + (6 * 10^{24} * \lt 0, 0, 0\gt ) - (10 * \lt -10, 0, 0\gt )}{6 * 10^{24}} \\ &= \frac{\lt 100, 0, 0\gt + \lt 100, 0, 0\gt }{6 * 10^{24}} \\ &= \lt 3.33 * 10^{-23}, 0, 0\gt m/s \end{aligned} }[/math]

The recoil velocity of the earth is too small for anyone to feel it--turns out if humans want to believe in something, they will sometimes ignore facts and do it anyway.

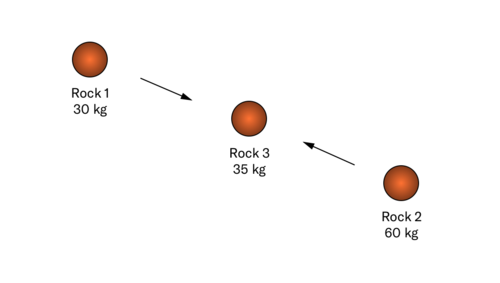
Question 3

Two rocks in space are approaching a third, stationary rock. Rock 1 has a mass of [math]\displaystyle{ 30 kg }[/math] and moves with a velocity [math]\displaystyle{ \lt 13, -10, -2\gt m/s }[/math]. Rock 2 has a mass of [math]\displaystyle{ 60 kg }[/math], and moves with a velocity [math]\displaystyle{ \lt -3, 23, 3\gt m/s }[/math]. Rock 3 has a mass of [math]\displaystyle{ 35 kg }[/math] and is stationary. The rocks collide at Rock 3's location.

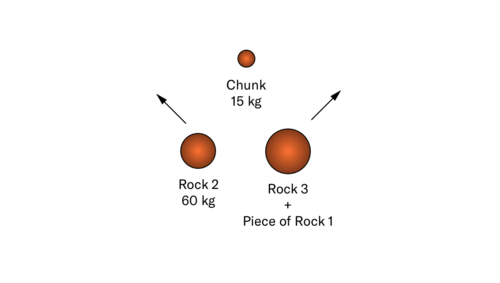
After the collision, it is observed that Rock 1 has embedded into Rock 3, which is now moving with a new velocity of [math]\displaystyle{ \lt 3, 5, 2\gt m/s }[/math], and that a chunk of mass [math]\displaystyle{ 15 kg }[/math] has broken off of the combined rock.

Rock 2, in the meantime, has a new velocity of [math]\displaystyle{ \lt -2, 12, 2\gt m/s }[/math].

What is the change in the internal energy [math]\displaystyle{ \Delta E_{internal} }[/math] in the system as a result of this three-way collision?

Answer 3

Due to the complexity of this question, we are going to use a computer to solve this problem. Conceptually, everything remains the same, but instead of computing things by hand, we're getting help from a computer. Feel free to solve it by hand if you want to! 

   # Define the initial masses/velocities of the rocks.
   mass_1_i = 30
   mass_2_i = 60
   mass_3_i = 35
   
   v_1_i = vector(13, -10, -2)
   v_2_i = vector(-3, 23, 3)
   v_3_i = vector(0, 0, 0)
   
   # Calculate the initial total momentum.
   total_p_i = (mass_1_i * v_1_i) + (mass_2_i * v_2_i) + (mass_3_i * v_3_i)
   
   # Calculate the masses/velocities of the rocks after the collision.
   mass_chunk = 15
   
   mass_2_f = 60
   mass_3_f = mass_1_i + mass_3_i - mass_chunk
   
   v_2_f = vector(-2, 13, 2)
   v_3_f = vector(3, 5, 2)
   
   # Calculate the velocity of the chunk. Remember that the momentum is conserved.
   v_chunk = (total_p_i - ((v_2_f * mass_2_f) + (v_3_f * mass_3_f))) / mass_chunk
   
   # Calculate the initial total kinetic energy.
   def kinetic_energy(mass, velocity):
       return 1/2 * mass * magnitude(velocity) ** 2
   k_tot_i = kinetic_energy(mass_1_i, v_1_i) \
           + kinetic_energy(mass_2_i, v_2_i) \
           + kinetic_energy(mass_3_i, v_3_i)
   
   # Calculate the final total kinetic energy.
   k_tot_f = kinetic_energy(mass_2_f, v_2_f) \
           + kinetic_energy(mass_3_f, v_3_f) \
           + kinetic_energy(mass_chunk, v_chunk)
   
   # Calculate the change in internal energy.
   d_e_internal = k_tot_f - k_tot_i

This Python snippet, when evaluated, will show that [math]\displaystyle{ \Delta E_{internal} = 5175 J }[/math].

Connectedness

As we mentioned in the introduction to this article, collisions are everywhere in our daily lives. Some examples are a bat colliding with a baseball in your neighbor's backyard, two cars crashing in the highway in front of you, and so on.

Depending on the nature of the collision we can usually guess whether it's an Elastic Collision or an Inelastic Collision, and reason about it. (If it's a car crash, things crumble, so there's increase in thermal energy, etc.)

Another very interesting application of collisions is in the field of astronomy. The universe is ever-changing and we never know what might come our way. A large meteor could be flying at the Earth with a very high speed and we could use our knowledge of collisions to find out how the Earth will move after the collision, what the temperature change of the area would be, and how the rest of the Earth would be effected by the collision. By using our collision skills, we could evacuate anyone who is prone to harm during the collision.

Since collisions are ubiquitous processes, knowledge about them is instrumental for any engineer who deals with the physical world.

History

We've mentioned that collisions are not special case events in Physics-- the fundamental principles apply fully for them, and we reason about them using these principles. Then it won't surprise us that the history of collisions is tangled with the history of the fundamental principles.

In 1661, Christiaan Huygens, a Dutch physicist, concluded that when a moving body struck a stationary object of equal mass, the initial moving body would lose all of its momentum while the second object would pick up the same amount of velocity that the moving body had before the collision. He also stated that the total "quantity of motion" should be the same before and after the collision. This was the first thought of the conservation of momentum.

In 1687, Sir Isaac Newton went a little further and stated in his third law of motion that the forces of action and reaction between two bodies are opposite and equal. Because of this law; the total momentum of a closed system is constant. Every force in the system has a reciprocal pair with an opposing direction, which implies that their momentas cancel out, keeping the total momentum constant.

In Ernest Rutherford's famous Gold Foil Experiment of 1899, he found out that the plum pudding model of the atom was inaccurate, and that there was a concentrated core at the center of the atom (nucleus) and a lot of empty space around. He didn't have access to the sophisticated tools/knowledge that we have now to assist in his discovery: he did this through investigating atomic collisions between alpha particles and gold foil. He shot alpha particles to a piece of thin gold foil, and observed that some of the particles were scattered through angles larger than 90 degrees during the collisions. Using collisions principles, he was then able to reason that the atom had most of its mass concentrated in a dense core, rather than spread out evenly throughout the atom as the plum pudding model suggested.

See also

Maximally Inelastic Collision, Inelastic Collisions, Elastic Collisions, Momentum Principle, Energy Principle, Kinetic Energy, Net Force.

Further reading

Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. 4th ed. Vol. 1. Hoboken, NJ: Wiley, 2015. Print. Matter and Interactions.

Ehrhardt, H., and L. A. Morgan. Electron Collisions with Molecules, Clusters, and Surfaces. New York: Plenum, 1994. Print.

References

Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. 4th ed. Vol. 1. Hoboken, NJ: Wiley, 2015. Print. Matter and Interactions.

"The Gold Foil Experiment." The Gold Foil Experiment. N.p., n.d. Web. 17 Apr. 2016.

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Collisions&oldid=29726"