Inelastic Collisions
Created by Csorensen6
Edited/Claimed by Jessica Ouyang, Fall 2018
Edited/Claimed by Vansh Kareer, Spring 2017
Edited/Claimed by Abigail Brady, Fall 2017
This topic covers the concept of inelastic collisions and the results of the collisions on the bodies involved. Included are the methods that can be applied to solve problems related to these types of collisions, along with worked examples.
The Main Idea
There are two types of collisions: inelastic and elastic. The big identifying characteristics of inelastic collisions that distinguish them from elastic collisions is that in inelastic collisions, the momentum of the interacting bodies are conserved, but the kinetic energy is not. This change in kinetic energy from initial to final states is what differentiates inelastic collisions from elastic collisions. Generally, the forces involved in an inelastic collisions are so large relative to external forces that those external forces can be ignored. Consequently, given that [math]\displaystyle{ ΔP_{system} = F_{net,ext}ΔT }[/math], if we approximate [math]\displaystyle{ F_{net,ext} }[/math]as zero, then [math]\displaystyle{ ΔP_{system} = 0 }[/math], and [math]\displaystyle{ P_i = P_f }[/math].
Because the final kinetic energy differs from the initial kinetic energy, inelastic collisions witness a change in the internal energy of the objects involved in the collision. A change in internal energy often manifests itself in the form of deformation, rotation, heat, vibration, explosions, or energy state excitation.
Types of Inelastic Collisions
One type of inelastic collisions is the maximally inelastic collision, also known as the perfectly inelastic collision, in which two objects collide and then remain connected for the duration of the observable interaction. This does not indicate an end to movement, as momentum must be conserved by the end of the interaction. See problem 1 for an example. More information about such problems can be found in the page Maximally Inelastic Collision.
Most inelastic collisions are considered partially inelastic collisions. In these types, two or more objects collide but do not stick together (unlike maximally inelastic collisions), but as a result of their collision, one or both begin to rotate, vibrate, deform, heat up, etc.
In these problems, there is a positive ΔEint and a negative ΔK, and Ki > Kf. An example of a typically inelastic collision is a car crash.
Explosions are a somewhat special case of inelastic collisions. In these types of problems, an object bursts apart, and some of its internal energy is converted into kinetic energy. As a result, ΔK is actually positive and ΔEint is actually negative, in that internal energy is used up in the course of the explosion and causes an increase in the speed of the particles involved. This can be seen in the relation Ki < Kf, wherein the change in internal energy of the lends itself to the increase in kinetic energy from Ki to Kf, which directly correlates to an increase in particle speed in the explosion's aftermath.
Mathematical Model
In inelastic collisions, the change in internal energy is equal to the negative change in kinetic energy. Based on these characteristics, and applying the momentum principle, a few basic equations can be set to outline an inelastic collision.
The picture below illustrates some characteristics of a typical, inelastic collision: a car crash.
In the car crash depicted above, there is a loss of kinetic energy, which is converted into internal energy in the form of produced heat and deformation of the car and the tree.
This is in accordance with the relation [math]\displaystyle{ ΔE_{internal} = -ΔK_{trans}=-0.5(mass)(Δvelocity)^2 }[/math].
A very simple way to approach many inelastic collision problems is using the conservation of momentum principle. Since the two objects would not bounce and thus stick together- they become one object in terms of calculations. So the final equation would be: [math]\displaystyle{ m_1v_1 + m_2v_2 = (m_1 + m_2)v_f }[/math].
Computational Model
Using the Collision Lab [1], you can model different scenarios for the inelastic collision. Such as when the two bodies have the same mass, or when one is moving at a higher speed than the other. This simulation can help visualize inelastic collisions under different circumstances.
Examples
Typical Process for Solving
In such problems, it is often necessary to apply both the momentum principle and the energy principle.
Momentum Principle: [math]\displaystyle{ p_{1f} + p_{2f} = p_{1i} }[/math]
Energy Principle: [math]\displaystyle{ K_{1f} + K_{2f} + E_{int,f} = K_{1i} + E_{int,i} }[/math]
As shown above, the change in internal energy is directly related to the change in kinetic energy, in the Energy Principle.
The steps for solving inelastic collision problems are often as follows:
1) Draw a picture of the initial and final states.
2) Given that collisions involve extremely large forces acting over short time intervals, it is accurate to say that [math]\displaystyle{ F_{net,ext} = 0 }[/math], because the external forces are typically much, much smaller than the internal forces involved in the collision.
3) Knowing that [math]\displaystyle{ F_{net,ext} = 0 }[/math], this means that momentum is conserved and that [math]\displaystyle{ P_f = P_i }[/math]. This comes from the momentum principle, in that [math]\displaystyle{ ΔP_{system} = F_{net,ext}ΔT }[/math], and if [math]\displaystyle{ F_{net,ext} }[/math] is zero, then the right side of that equation is also zero.
4) Next, knowing that [math]\displaystyle{ P_f = P_i }[/math], you can solve for any unknown velocities of the objects involved via the momentum principle.
5) Having determined the velocity of each object, you can then determine the initial and final kinetic energies of the system using [math]\displaystyle{ K = (1/2)m|v|^2 }[/math] for each object.
6) Next, you can find the change in kinetic energy, or ΔK, and this will be equal to the negative change in the internal energy (whether it be heat, rotation, etc.) gained by the objects in the course of the collision. In other words [math]\displaystyle{ ΔE_{int} = -ΔK }[/math].
Simple
Question
Block A moves on a friction-less surface at a speed of 5 m/s towards block B. Block B is moving towards Block A at a speed of 2 m/s. Block A has a mass of 2 kg and block B has a mass of 1.5 kg. Assume the blocks are moving directly toward each other in the x direction and stick together on colliding. What is the speed of the blocks after the collision?
Answer
Using conservation of momentum, we can say that the momentum of the two blocks before the collision is equal to the momentum of the blocks after the collision.
[math]\displaystyle{ p_{1i} + p_{2i} = p_{f} }[/math]
[math]\displaystyle{ m_{A}v_{A,i} + m_{B}v_{B,i} = m_{f}v_{f} }[/math]
[math]\displaystyle{ (2)(5) + (1.5)(2) = (2 + 1.5)(v_f) }[/math]
[math]\displaystyle{ 10 + 3 = 3.5v_f }[/math]
[math]\displaystyle{ v_f = 3.714 m/s }[/math]
Middling
Question
There are two hockey pucks traveling across the surface of a frozen pond. The first puck has a mass of 0.15 kg and is moving with a velocity of <2.5, 3.4, 0> m/s. The second puck has a mass of 0.13 kg and is moving with a velocity of <-3.1, 1.7, 0> m/s. After colliding, the first puck then has a velocity of <-1.9, 3.0, 0> m/s. (Reference the image below).
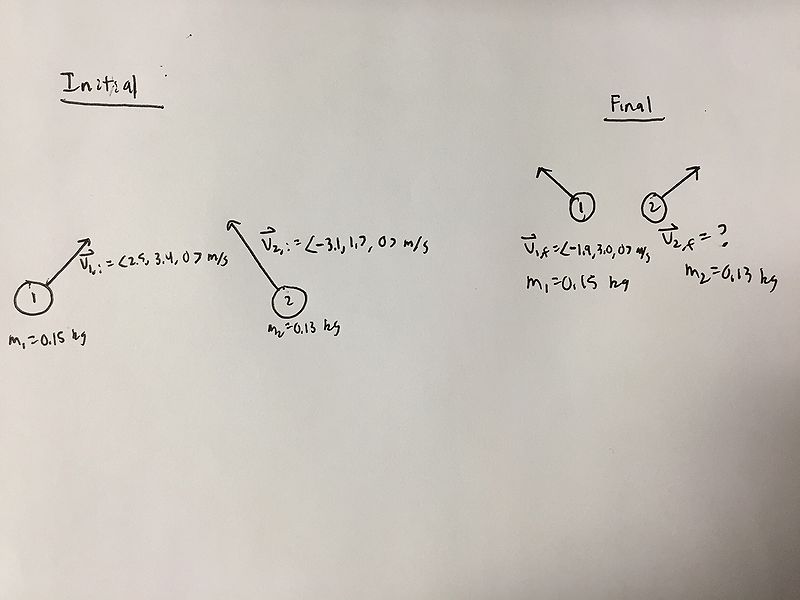
a) What is the velocity of the second puck after the collision?
b) What is the initial kinetic energy?
c) What is the final kinetic energy?
d) What is the change of the internal energy of the two pucks?
Answer
a)
ΔP = Pf - Pi = Fnet,ext*ΔT = 0 Pi = Pf
0.15kg<2.5, 3.4, 0> m/s + 0.13kg<-3.1, 1.7, 0> m/s = 0.15kg<-1.9, 3.0, 0> m/s + 0.13kg*v <-0.028, 0.731, 0> kg*m/s = <-0.285, 0.45, 0> kg*m/s + 0.13kg*v <0.257,0.281,0> kg*m/s = 0.13kg*v
v = <1.977, 2.162, 0> m/s
b)
K = (1/2)*m*|v|^2
|v| = (vx^2 + vy^2 + vz^2)^(1/2)
|v|^2 = vx^2 + vy^2 + vz^2
Ki = (1/2)*0.15kg*((2.5 m/s)^2 + (3.4 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((-3.1 m/s)^2 + (1.7 m/s)^2 + (0 m/s)^2)
Ki = 1.336 J + 0.813 J
Ki = 2.149 J
c)
K = (1/2)*m*|v|^2 |v| = (vx^2 + vy^2 + vz^2)^(1/2) |v|^2 = vx^2 + vy^2 + vz^2
Kf = (1/2)*0.15kg*((-1.9 m/s)^2 + (3.0 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((1.977 m/s)^2 + (2.162 m/s)^2 + (0 m/s)^2) Kf = 0.946 J + 0.558 J
Kf = 1.504 J
d)
ΔE = Q + W = ΔK + ΔEinternal + ΔU + ΔErest ΔE = ΔK + ΔEinternal = 0 = Kf - Ki + ΔEinternal
1.504 J - 2.149 J + ΔEinternal = 0 -0.645J + ΔEinternal = 0
ΔEinternal = 0.645 J
Question
A bullet of mass 0.071 kg traveling horizontally at a speed of 100 m/s embeds itself in a block of mass 2 kg that is sitting at rest on a nearly frictionless surface.
(a) What is the speed of the block after the bullet embeds itself in the block?
(b) Calculate the kinetic energy of the bullet plus the block before the collision:
(c) Calculate the kinetic energy of the bullet plus the block after the collision:
(d) Was this collision elastic or inelastic?
(e) Calculate the rise in thermal energy of the bullet plus block as a result of the collision:
(f) What was the transfer of energy Q (microscopic work) from the surroundings into the block+bullet system during the collision? (Remember that Q represents energy transfer due to a temperature difference between a system and its surroundings.)
Answer
a)
ΔP = Pf - Pi = Fnet,ext*ΔT = 0 pi1+pi2=pf m1*v1+m2*v2=mf*vf vf=(m1*v1+m2*v2)/mf vf=(0.071 kg*100 m/s+2 kg*0 m/s)/(2.071 kg) vf=3.43 m/s
b)
Ki=0.5*m1*v1i^2+0.5*m2*v2i^2 Ki=0.5*0.071 kg*(100 m/s)^2+0.5*(2 kg)*(0 m/s)^2 Ki=355 J
c)
Kf=0.5*mf*vf^2 Ki=0.5*2.071 kg*(3.43 m/s)^2 Ki=12.18 J
d)
Due to the fact that the final kinetic energy is less than the initial kinetic energy (change in kinetic energy), while the momentum of the interaction is conserved, the interaction can be said to be inelastic. The result of the change in kinetic energy is a rise in internal/thermal energy.
e)
ΔEthermal,bullet + ΔEthermal,block = ΔK=Ki-Kf ΔEthermal,bullet + ΔEthermal,block = 355 J-12.18 J ΔEthermal,bullet + ΔEthermal,block = 342.8 J
e)
As the collision takes place in a closed system, and the collision considers forces that render frictional forces by surroundings negligible, there is no transfer of energy Q between the surroundings and the system. Q=0 J
Difficult
Question
A lit firework of mass 15 kg is launched into the sky with an initial velocity of <10,17,0> m/s. Eventually, its fuse burns up and the firework explodes, bursting into four parts. One piece has a mass of 3 kg and a velocity of <8,7,0> m/s. Another has a mass of 4 kg and a velocity of <15,0,0> m/s. The third has a mass of 3.5 kg and a velocity of <12,-5,0> m/s.
Reference the picture below.
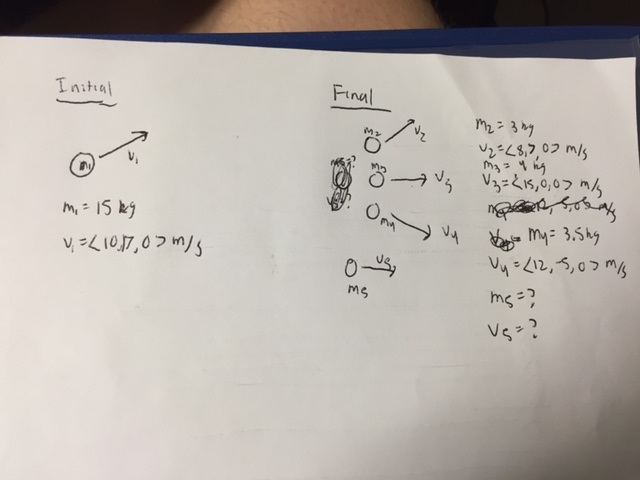
a) What is the mass of the fourth piece?
b) What is the momentum and velocity of that piece?
c) What is the change in internal energy?
d) Justify the sign of the answer found in part c).
Answer
a)
m1 = m2 + m3 + m4 + m5 15 kg = 3 kg + 4 kg + 3.5 kg + m5 15 kg = 10.5 kg + m5 m5 = 4.5 kg
b)
ΔP = Pf - Pi = Fnet,ext*ΔT = 0 Pi = Pf 15 kg <10,17,0> m/s = 3 kg <8,7,0> m/s + 4 kg <15,0,0> m/s + 3.5 kg <12,-5,0> m/s + p5 <150,255,0> kg*m/s = <24,21,0> kg*m/s + <60,0,0> kg*m/s + <42,-17.5,0> kg*m/s + p5 <150,225,0> kg*m/s = <126,3.5,0> kg*m/s + p5 p5 = <24,251.5,0> kg*m/s
p = mv p5 = m5v5 <24,251.5,0> kg*m/s = 4.5kg*v5 v5 = <5.33,55.89,0> m/s
c)
ΔE = Q + W = ΔK + ΔEinternal + ΔU + ΔErest = 0 ΔE = ΔK + ΔEinternal = 0 = Kf - Ki + ΔEinternal ΔEinternal = Ki - Kf
ΔEinternal = (1/2)(15)(10^2 + 17^2 + 0^2) - (1/2)(3)(8^2 + 7^2 + 0^2) - (1/2)(4)(15^2 + 0^2 + 0^2) - (1/2)(3.5)(12^2 + (-5)^2 + 0^2) - (1/2)(4.5)(5.33^2 + 55.89^2 + 0^2) ΔEinternal = 2971.5 - 169.5 - 450 - 295.75 - 7092 ΔEinternal = -5036 J
d)
The final kinetic energy is greater than the initial kinetic energy, and this is because by exploding, some of the internal energy stored in the firework was released and then harnessed as kinetic energy. Consequently, the change in internal energy is negative.
Connectedness
The science of collisions and the study of momentum are especially prominent when it comes to the sport of football, and particularly in regards to concussions, or traumatic brain injuries sustained due to hard blows to the head. Significant research within the biomedical field is being conducted into how to reduce concussion frequency and severity, and this often entails specifically designing helmets to minimize the impact of high-speed, hard-hitting tackles. This research has come to greater prominence with the relatively recent discovery of the role football plays in the acquisition of CTE, a degenerative disease which slowly causes the loss of cognitive function, similar to dementia, and is especially prominent among football players and other athletes who suffer repeated head trauma.
The concepts presented through collisions are also the founding physics principles for studying car crashes, or car safety, as well as other real world events that contain collisions. By using the mathematical models introduced earlier, studies can be done to improve the user experience and overall safety of many things including vehicles.
.jpg)
History
The idea of inelastic collisions is rooted in the conservation of linear momentum, which is implied by Newton's Laws. Newton published his book, the Philosophiae Naturalis Principia Mathematica, in 1687. This book, commonly known as Principia, described Newton’s findings on collisions and laid a foundation for the different types of collisions we study today.
The history of collisions in modern physics starts with Rutherford’s Gold Foil experiment. He found that while they did not touch, the alpha particles and the gold nucleus collided elastically. It is essential that the collision was elastic, in that it gives us the famous scatting pattern and led to the discovery of the positively charged nucleus.
See Also
Further reading
For more information about the momentum principle, check out this page!
For more on the energy principle, check here:
If you want to learn more about elastic or maximally inelastic collisions, check out these pages:
External links
A different explanation of inelastic collisions
A Khan Academy video on elastic and inelastic collisions
References
Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print