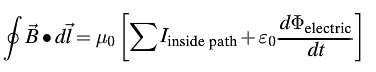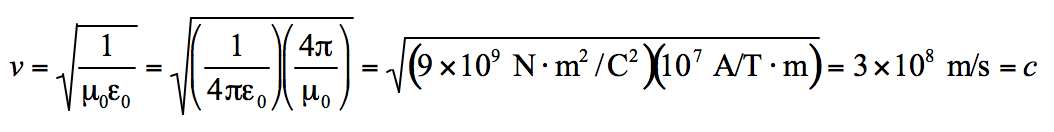Ampere-Maxwell Law: Difference between revisions
No edit summary |
|||
| Line 18: | Line 18: | ||
*B is the magnetic field, | *B is the magnetic field, | ||
*dl is the change in path, | *dl is the change in path, and | ||
* | *the sum of I is the sum of the charges inside the path. | ||
==Examples== | ==Examples== | ||
Revision as of 22:35, 29 November 2017
Claimed by Maria Rivero Claimed by Yeon Jae Cho (FALL 2016)
Claimed by Stella Chen (Fall 2017)
Ampere-Maxwell Law
The Ampere-Maxwell Law expands on Ampere's Law relating magnetic field and current on a closed loop. The Ampere-Maxwell Law accounts for situations in which the electric field for a certain system is changing with regard to time.
Ampere-Maxwell Law is also known as the Ampere's Circuital Law, and it shall not be confused with Ampere's Force Law.
Mathematical Model
Where
- B is the magnetic field,
- dl is the change in path, and
- the sum of I is the sum of the charges inside the path.
Examples
Simple
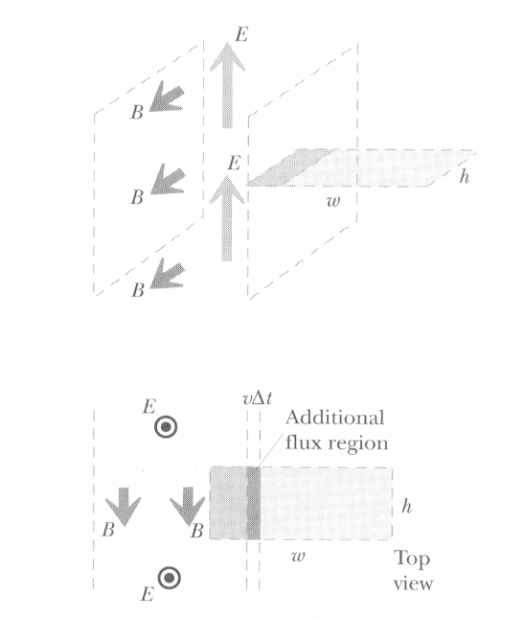
Pick a closed, rectangular path in the xz plane with a height h and a width w. Calculate the speed v of the slab.
At a time change in t, we can calculate the area as the height (h) times the speed over the change in time. ⩟ A = v (⩟ t) h Because the electric field is constant in this region we can also calculate the change in electric flux over time as Evh(⩟ t) /(⩟ t) which is the same as Evh Calculating the path integral for the magnetic field we get that ∮B . dl = Bh cos 0 = Bh An important thing to notice is that there is no current I, so, using the Ampere-Maxwell Law we can see that
Bh = μ. [I+ ε. (vEh)]
but since there is no current,
B = μ. ε. (vE)
From Faraday's law we get that the emf equals the rate of change of the magnetic flux: Eh = Bvh
Substituting E = Bv into our previous equation we get that
B = μ. ε. (v(vB))
Solving for v we get that:
From the picture we see that the speed of light relates the a time varying electric and magnetic field.
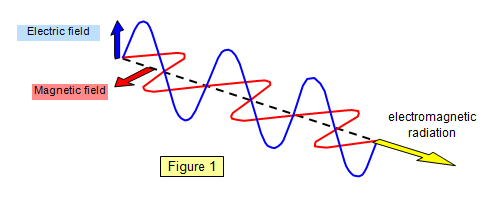
What this implies
In the example above we saw that the speed of light relates the a time varying electric and magnetic field. This translates to the fact that an electromagnetic wave propagates at the speed of light.
Conceptual Question
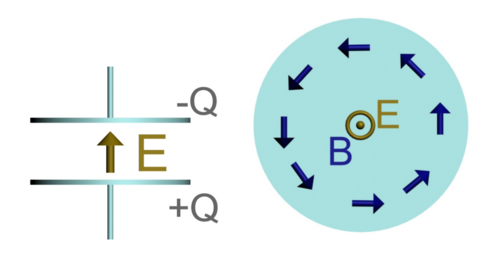
The plot above shows a side and a top view of a capacitor with charge Q with electric and magnetic fields E and B at time t. The charge Q is:
1) Increasing in time
2) Decreasing in time
3) Constant in time
4) I don't know
Answer:
The unit vector N points out of the plane. Given that the magnetic field curls clockwise, the electric flux would be positive and decreasing. Hence E is decreasing. Thus Q must be decreasing, since E is proportional to Q.
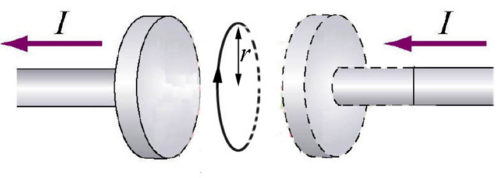
Consider a circular capacitor, with an Amperian circular loop (radius r) in the plane midway between the plates. When the capacitor is charging, the line integral of the magnetic field around the circle (in direction shown) is
1) Zero
2) Positive
3) Negative
4) Can’t tell
Answer:
One thing to notice is that there is no enclosed current through the disk. When integrating in the direction shown, the electric flux is positive. Because the plates are charging, the electric flux is increasing. Therefore the line integral is positive.
Connectedness
How is this topic connected to something that you are interested in?
I am particularly interested in understanding medicine and how using all these waves we can help doctors understand and see different aspects of the human body.
How is it connected to your major?
I do not know how this would be connected to Industrial Engineering, however it is very useful for Electrical Engineering and Mechanical Engineering.
Is there an interesting industrial application?
As I mentioned before, this is very useful in medicine when creating the images for the MRI scanners in hospitals. But it is also important to generate electricity, to build computers and phones, etc. More generally, Maxwell's equations work for all devices that use electricity and magnets.
History
You may remember Ampere's Law equation from chapter 21 of the textbook (Ampere's Law). This equation had to be modified to address time-varying electric fields and their associated magnetic fields. If Ampere's Law were applied to a situation with a time-varying electric field, at different points along the chosen Amperian path, different answers for the current enclosed would be obtained. In the same way that Faraday discovered that a time-varying magnetic field is accompanied by an electric field, James Clerk Maxwell resolved this issue when he discovered that an electric field that changed with time was accompanied by a resulting magnetic field. Specifically, when the plates of a capacitor grows as the capacitor is charged, the electric field changes (with time) which produces a magnetic field.
See also
The Ampere-Maxwell Law relates to the other Maxwell equations:
It might also help to read up on Maxwell's Electromagnetic Theory
Also for continuity purposes, it can be helpful to look at the incomplete Ampere's Law:
Further Reading
Matter and Interactions: Volume 2 by Ruth Chabay and Bruce Sherwood (4th Edition)
External Links
Maxwell's Equations: http://study.com/academy/lesson/maxwells-equations-definition-application.html
James Maxwell Biography: http://www.biography.com/people/james-c-maxwell-9403463
References
http://bulldog2.redlands.edu/fac/eric_hill/Phys232/Lectures/Ch%2023%20lect%201.pdf http://ocw.mit.edu/high-school/physics/exam-prep/electromagnetism/maxwells-equations/ http://ocw.mit.edu/courses/physics/8-02-physics-ii-electricity-and-magnetism-spring-2007/readings/summary_w13d1.pdf http://www.schoolphysics.co.uk/age16-19/Wave%20properties/Wave%20properties/text/Electromagnetic_radiation/index.html