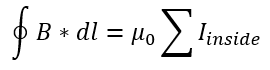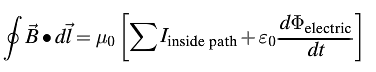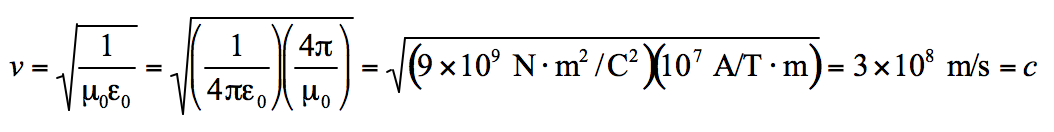Ampere-Maxwell Law

Claimed by Maria Rivero Claimed by Yeon Jae Cho (FALL 2016)

Claimed by Stella Chen (Fall 2017)

Ampere-Maxwell Law

The Ampere-Maxwell Law expands on Ampere's Law relating magnetic field and current on a closed loop. Ampere's Law:

allowed us to explore the relationship between current and magnetic field on a chosen closed loop called an "Amperian path". However, for certain examples in which electric field varies with time, simply using Ampere's Law is not sufficient. The Ampere-Maxwell Law accounts for these situations and establishes that a time dependent electric field is associated with a corresponding magnetic field.

The Ampere-Maxwell Law is also known as the Ampere's Circuital Law, and should not be confused with Ampere's Force Law.

Mathematical Model

Where

B is the magnetic field,

dl is the change in path, and

the sum of I is the sum of the charges inside the path.

Examples

Simple

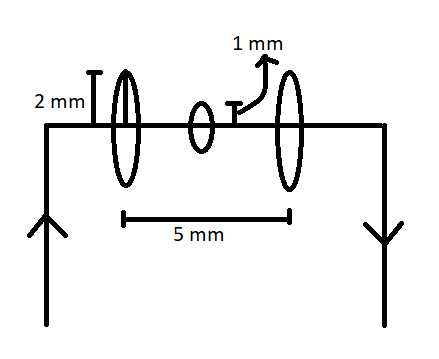
Question: A 30-A current is charging a capacitor that has circular plates 5 mm in diameter. The plate separation is 4 mm. What is the magnetic field between the plates 1 mm from the center?

Answer:

[math]\displaystyle{ \oint \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \mu_0 ε_0 \frac{d\Phi_E}{dt} }[/math]

this is simply the Ampere-Maxwell Law

[math]\displaystyle{ \oint \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \mu_0 ε_0 \frac{d}{dt}(\frac{q \pi r^2}{ε_0 A}) }[/math]

this step breaks down the electric flux part of the equation

[math]\displaystyle{ \mathbf{B} \cdot 2\pi r = \mu_0 ε_0 \frac{dq}{dt}\frac{\pi r^2}{ε_0 A} }[/math]

Since the path is a circle, replace dl with circumference of the circle

[math]\displaystyle{ \mathbf{B} = \frac{\mu_0 I r}{2A} = \frac{\mu_0 I r}{2 \pi R^2} }[/math]

Continue to simplify and plug in I for dq/dt and plug in values (where I = 30 A, r = 1 mm, R = 2.5 mm)

[math]\displaystyle{ \mathbf{B} = 1 mT }[/math]

Middling

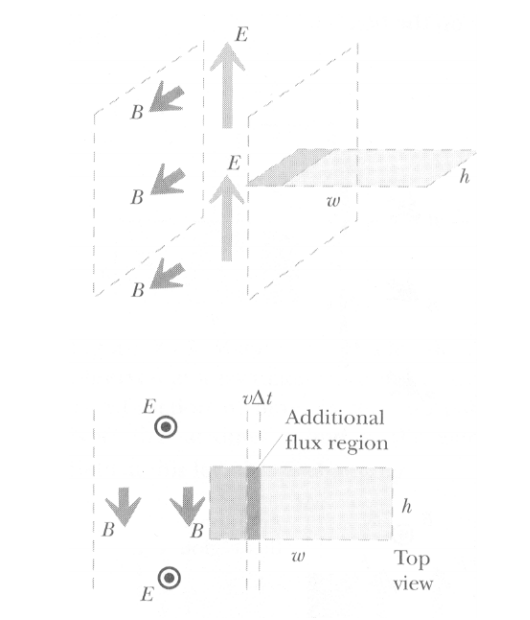
Pick a closed, rectangular path in the xz plane with a height h and a width w. Calculate the speed v of the slab.

At a time change in t, we can calculate the area as the height (h) times the speed over the change in time. ⩟ A = v (⩟ t) h Because the electric field is constant in this region we can also calculate the change in electric flux over time as Evh(⩟ t) /(⩟ t) which is the same as Evh Calculating the path integral for the magnetic field we get that ∮B . dl = Bh cos 0 = Bh An important thing to notice is that there is no current I, so, using the Ampere-Maxwell Law we can see that

Bh = μ. [I+ ε. (vEh)]

but since there is no current,

B = μ. ε. (vE)

From Faraday's law we get that the emf equals the rate of change of the magnetic flux: Eh = Bvh

Substituting E = Bv into our previous equation we get that

B = μ. ε. (v(vB))

Solving for v we get that:

The example shows that the speed of light relates the a time varying electric and magnetic field.

What this implies

In the example above we saw that the speed of light relates a time varying electric and magnetic field. This translates to the fact that an electromagnetic wave propagates at the speed of light.

Difficult

Question 1: First find the line integral of B around a loop of radius R located just outside the left capacitor plate.

Answer:

[math]\displaystyle{ \int \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \mu_0 I(t) }[/math]

Question 2: Now find an expression for the same line integral of B around the same loop located just outside the left capacitor plate as before. Use the surface that passes between the plates of the capacitor, where there is no conduction current. This should be found by evaluating the amount of displacement current in the Ampère-Maxwell law above.

Answer:

[math]\displaystyle{ \Phi_E = \int E \cdot dA = A E(t) }[/math]

[math]\displaystyle{ I = ε_0 d \frac{(AE(t))}{dt} = A ε_0 \frac{dE(t)}{dt} }[/math]

[math]\displaystyle{ \int \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \mu_0 I }[/math]

[math]\displaystyle{ \int \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \mu_0 A ε_0 \frac{dE(t)}{dt} }[/math]

Question 3: Express the normal current in terms of the charge on the capacitor plate.

Answer:

[math]\displaystyle{ I = ε_0 \frac{d\frac{q}{ε_0}}{dt} }[/math]

the expression for the normal current is:

[math]\displaystyle{ I = \frac{dq(t)}{dt} }[/math]

the current is directly related to charge on left capacitor plate

Conceptual Questions

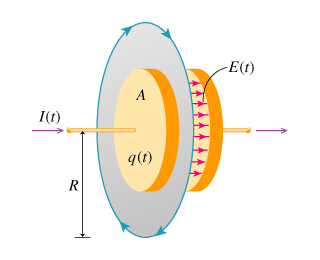
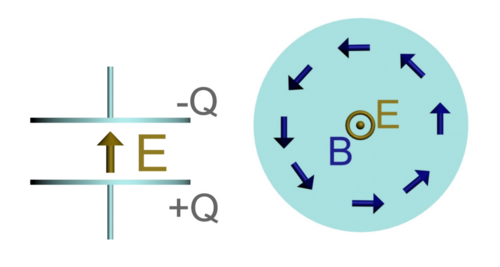
The plot above shows a side and a top view of a capacitor with charge Q with electric and magnetic fields E and B at time t. The charge Q is:

1) Increasing in time

2) Decreasing in time

3) Constant in time

4) I don't know

Answer:

The unit vector N points out of the plane. Given that the magnetic field curls clockwise, the electric flux would be positive and decreasing. Hence E is decreasing. Thus Q must be decreasing, since E is proportional to Q.

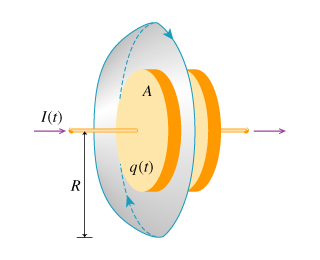
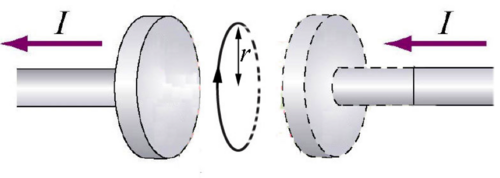
Consider a circular capacitor, with an Amperian circular loop (radius r) in the plane midway between the plates. When the capacitor is charging, the line integral of the magnetic field around the circle (in direction shown) is

1) Zero

2) Positive

3) Negative

4) Can’t tell

Answer:

One thing to notice is that there is no enclosed current through the disk. When integrating in the direction shown, the electric flux is positive. Because the plates are charging, the electric flux is increasing. Therefore the line integral is positive.

Connectedness

The Ampere-Maxwell Law is extremely useful in many aspects of life. It relates current and time-varying electric fields and allow us to derive a magnetic field from these situations. The Ampere-Maxwell Law can help with understanding and building generators and transformers.

History

You may remember Ampere's Law equation from chapter 21 of the textbook (Ampere's Law). This equation had to be modified to address time-varying electric fields and their associated magnetic fields. If Ampere's Law were applied to a situation with a time-varying electric field, at different points along the chosen Amperian path, different answers for the current enclosed would be obtained. In the same way that Faraday discovered that a time-varying magnetic field is accompanied by an electric field, James Clerk Maxwell resolved this issue when he discovered that an electric field that changed with time was accompanied by a resulting magnetic field. Specifically, when the plates of a capacitor grows as the capacitor is charged, the electric field changes (with time) which produces a magnetic field.

Ampere-Maxwell Law

Contents