Maxwell's Electromagnetic Theory

Claimed by Griffin Bonnett Spring 2017. Edited by Danielle Saracino Spring 2018. Claimed by Braeden Collins Fall 2018.Claimed by Carissa Lucas Fall 2023.

Written by Megan Sales. Edited by Grace Newville.

A general description of "A Dynamical Theory of the Electromagnetic Field," proposed by Maxwell in 1865.

The Main Idea

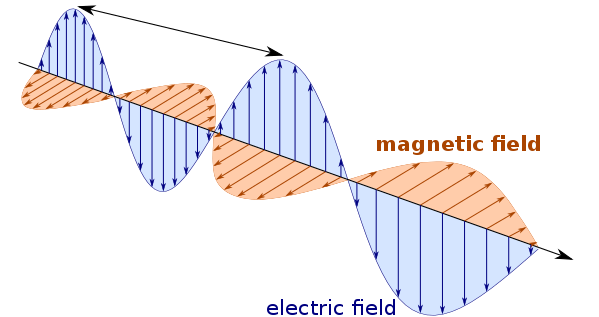
Source: https://commons.wikimedia.org/wiki/File:Electromagnetic_wave_EN.svg (Used through Creative Commons License)

"Light consists in transverse undulations of the same medium which is the cause of electric and magnetic oscillations" - James Maxwell

In short, Maxwell suggested that light, an electric field, and a magnetic field could all be explained in a single electromagnetic theory. Maxwell’s theory describes that the electric and magnetic fields which were once thought to be two separate fields are actually distinctly different, paired components of the same field. James Clerk Maxwell developed his theory, with the help of Einstein's prior special relativity theory, that brought together two of the main concepts discussed in this class: electric fields and magnetic fields. These fields have largely been discussed separately, but when Maxwell's Equations were first introduced, the connections became more and more apparent. Maxwell's Electromagnetic Theory brought about the deep relation between electric and magnetic fields, i.e. electromagnetic fields. Maxwell's theory proposed that electric and magnetic fields move as waves at the speed of light. This was the first time electricity, magnetism, and light had been related in such a way. Together, the four equations give a complete description of all of the spatial patterns of magnetic and electric fields that are possible anywhere in space for many different varying scenarios.

Brief Overview of Maxwell's Electromagnetic Theory: https://www.youtube.com/watch?v=50v75xPfhQI

A Mathematical Model

Maxwell Equations:

These are the four complete Maxwell Equations in their integral form.

1) Gauss's Law relates electric field to the charge enclosed by a "Gaussian Surface." The integral represents the sum of electric flux, so by finding this and multiplying by epsilon-zero, the charge enclosed by the surface may be calculated. The electric flux out of any closed surface is proportional to the total charge enclosed within the surface.

2) Gauss's Law for magnetism states that the sum of magnetic flux for a specific area is equal to zero. This amounts to a statement about the sources of magnetic field. For a magnetic dipole, any closed surface the magnetic flux directed inward toward the south pole will equal the flux outward from the north pole.

3) Faraday's Law directly relates electric and magnetic fields by being able to find the non-Coulomb Electric field that is produced due to a magnetic field and current. The line integral of the electric field around a closed loop is equal to the negative of the rate of change of the magnetic flux through the area enclosed by the loop.

4) Ampere-Maxwell Law is perhaps the most complex of Maxwell's Equations, and involves the derivative of electric flux. In the case of static electric field, the line integral of the magnetic field around a closed loop is proportional to the electric current flowing through the loop.

These are the four complete Maxwell Equations in their differential form.

A Computational Model

Maxwell's equations can be used to model a multitude of scenarios, but the key idea is that a time-varying magnetic field is associated with an electric field and vice versa. This leads to the concept that by solving the partial differential equations given by these four equations, all fields traveling through space may be modeled, but for most cases the calculations are so complex that they must be done computationally.

Here is a model of the electric and magnetic waves that are described in Maxwell's theory, note that they are perpendicular to each other and oscillate together. Source Code: https://trinket.io/glowscript/fa14ed42b6?toggleCode=true (Made by Carissa Lucas, a Georgia Tech Student)

Check out this resource for several interesting demonstrations.

Examples

Maxwell's 1st Equation (Gauss's Law for Electric Fields)

Problem

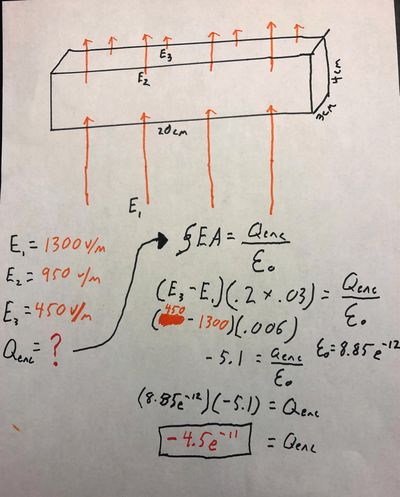
An electric field has been measured to be vertically upward everywhere on the surface of a box 20 cm long, 4 cm high, and 3 cm deep, shown in the figure. All over the bottom of the box E = 1300 V/m, all over the sides E = 950 V/m, and all over the top E = 450 V/m.

Find the charge Q enclosed by the box.

Solution

Creater by Braeden Collins, a Georgia Tech Student

Maxwell's 2nd Equation (Gauss's Law for Magnetic Fields)

Problem

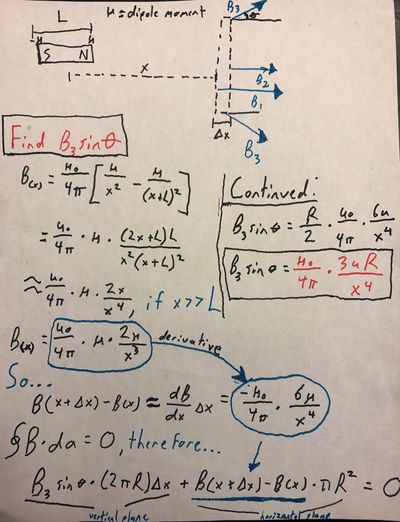
Apply Gauss's law for magnetism to a thin disk of radius R and thickness Δx located where the current loop will be placed. Use Gauss's law to determine the component of the magnetic field that is perpendicular to the axis of the magnet at a radius R from the axis. Assume that R is small enough that the component of magnetic field is approximately uniform everywhere on the left face of the disk and also on the right face of the disk (but with a smaller value). The magnet has a magnetic dipole moment μ. (See illustration in solution)

Find B₃sinθ.

Solution

Created by Braeden Collins, a Georgia Tech Student

Maxwell's 3rd Equation (Faraday's Law)

Problem

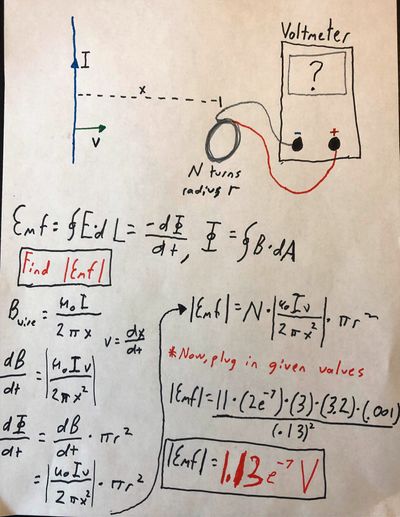
At a particular instant, a long straight wire carrying current 3A is moving with speed 3.2m/s toward a small circular coil of wire with a radius of 0.032m containing 11 turns, which is attached to a voltmeter as shown. The long wire is in the plane of the coil. (Only a small portion of the wire is shown in the picture below.) The distance from the wire to the center of the coil is 0.13m.

Find the magnitude of the reading on the voltmeter, and the direction of the current.

Solution

Created by Braeden Collins, a Georgia Tech Student

The direction of the current in the coil is counter-clockwise. This is because the direction of dB/dt is into the page, which is determined by pointing your thumb in the direction of I and curling your fingers to find B, and then using the fact that the wire is moving towards the loop to determine that it is growing larger over time. In order to counter-act this, the current produced in the coil will make a magnetic field out of the page. By applying right-hand rule again, you can determine that the current must go counter-clockwise to do this.

Gauss's Law Example

https://www.youtube.com/watch?v=c0S7U6uldsc

Derivation

Lengthy, but very informative:

https://www.youtube.com/watch?v=AWI70HXrbG0

Connectedness

Maxwell’s theory proved that electric and magnetic forces are not separate, but different versions of the same thing, the electromagnetic force. This became a motivation to attempt to unify the four basic forces in nature—the gravitational, electrical, strong, and weak nuclear forces.

Although changing electric fields create relatively weak magnetic fields that could not be detected during Maxwell’s lifetime, he realized they existed. He predicted that these changing fields would propagate from the source like waves generated on a lake by a jumping fish. Maxwell concluded that light is an electromagnetic wave having such wavelengths that it can be detected by the eye.

This video shows the derivation of the equations for thermodynamics, something a lot of students will use here at Georgia Tech if they take Thermodynamics.

Maxwell's equations also have a direct industrial application. They are used in magnetic machines and to accurately predict electrical machine performance. They also led to the development of the Maxwell stress tensor.

History

While in Copenhagen in 1820 Hans Christian Oersted embarked on a series of experiments in which he hoped to connect magnetism and electricity. This became an early inspiration for Maxwell’s work as well as many other physicists hoping to discover the fundamental nature of this “mysterious connection.”

A decade after Oersted’s experiment, Michael Faraday successfully converted electric energy into magnetic energy using an insulated wire and a galvanometer. This experiment was later used in a paper ‘On Faraday’s Lines of Force’ which derived electric and magnetic equations by comparing the flow of liquid to lines of electrical and magnetic force.

When James Clerk Maxwell came out with his paper, "A dynamical theory of the electromagnetic field," in 1865, it was found hard to understand and widely ignored. Even so, it is one of the most important pieces of theory in our history. He himself downplayed the importance of his theory, putting more emphasis on Kelvin's vortex theory during his own address. Furthermore, it was hard to grasp the concept of intangible fields. Scientists, including Maxwell, tried to picture fields as tangible structures, but to use these mechanical models with the Maxwell equations, they had to be exceedingly complicated. Later, other physicists such as Hertz, Lorentz, and Einstein clarified his theory.

When the paper first was written, it was read to the Royal Society. It was next read and reviewed by many other notable physicists, all prior to its publication. Even once it was published, very few copies were produced.

There were originally 20 equations. These were reduced by Heaviside into 8 equations, and these later became the four equations we are familiar with.

Impact

Maxwell was the first to show how to calculate stresses in framed arch and suspension bridges.

He invented the term "curl" for the vector operator that appears in his equations for the electromagnetic field.

Maxwell postulated that light is a form of electromagnetic radiation exerting pressure and carrying momentum. He provided the basis for Einstein's work on relativity from which the relationship between energy, mass and velocity contributed to the theory underlying the development of atomic energy.

Maxwell made fundamental contributions to the development of thermodynamics. He was also a founder of the kinetic theory of gases. This theory provided the new subject of statistical physics, linking thermodynamics and mechanics, and is still widely used as a model for rarefied gases and plasmas.

The discovery of electromagnetic radiation led to the development of radio and infra-red telescopes, currently exploring the farthest reaches of space.