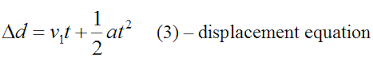Kinematics
This page describes the field of kinematics and presents some of the most important kinematic equations.
The Main Idea
The field of kinematics is the study of particle motion from a mathematical rather than physical point of view. More specifically, it studies the relationships between time and the position, velocity, and acceleration of particles, without regard for the forces that cause the acceleration. The equations that describe these relationships are called the kinematic equations, which are useful tools and the subject of most of this page. Often, these kinematic equations are used in combination with other branches of physics to predict the motion of an object at different points in time. For example, non-kinematic equations might be used to calculate the magnitude and direction of a force acting on a particle, and about the acceleration that the particle undergoes as a result. These equations are not kinematic because they describe the causes and effects of forces. Then, kinematic equations might be used to calculate the position of the particle as a function of time based on the acceleration found. These equations are kinematic because they relate position, acceleration, and time.
A Mathematical Model
Quantities of Kinematics
In order to understand the kinematic equations, the quantities they relate must be understood. The following are the quantities that the kinematic equations deal with:
- Time ([math]\displaystyle{ t }[/math]) Time is (in classical physics) a universal scalar variable whose value continually increases.
- Position ([math]\displaystyle{ \vec{r} }[/math]) The position of a particle is a property of that particle describing where it can be found in space. It is a vector quantity; three components are necessary to fully describe the position of a particle because our universe is three-dimensional. In Cartesian coordinates, these components are the x, y, and z coordinates. This is called motion.
- Velocity ([math]\displaystyle{ \vec{v} }[/math]) The velocity of a particle is the rate at which the particle's position changes over time. In calculus terms, it is the first time derivative of position, which you will recall is a function of time. The derivative of a vector is itself a vector, so velocity is a vector quantity. This makes sense because the position of a particle changes with both speed (the magnitude of velocity) and direction.
- Acceleration ([math]\displaystyle{ \vec{a} }[/math]) The acceleration of a particle is the rate at which the particle's velocity changes over time. In calculus terms, it is the first time derivative of velocity, and the second time derivative of position. Like position and velocity, acceleration is a vector, since the velocity vector changes with both speed and direction. Acceleration is caused by force, but this relationship lies outside the field of kinematics, which is concerned only with the relationship acceleration has with the other quantities listed here.
- Subsequent Time Derivatives of Position (less common) The "jerk" of a particle is the first time derivative of acceleration, the second time derivative of velocity, and the third time derivative of position. The fourth, fifth, and sixth time derivatives of position are "snap", "crackle", and "pop" respectively. These also fall in the realm of kinematics, but they can be difficult to develop an intuition for. Kinematic equations involving these quantities are not necessary for this course, do not appear on this page, and are rarely used by anyone. These quantities are only listed here to improve your understanding of what the field of kinematics does and does not encompass.
Many of the values listed above depend on the Frame of Reference, or coordinate system, chosen because the reference frame defines which points in space and time are considered x = 0, y = 0, z = 0, and t = 0. The following kinematic equations assume a reference frame of arbitrary spatial origin but with time t=0 defined as the time at which the particle is in its initial position. This assumption is made to avoid having to write [math]\displaystyle{ \Delta t }[/math] instead of [math]\displaystyle{ t }[/math] everywhere the time variable occurs, and because other definitions of t=0 are rarely used.
Subscripts of i and f respectively denote the initial and final values of these quantities over some time interval, the beginning of which is t=0.
Some of the kinematic equations make use of the average velocity ([math]\displaystyle{ \vec{v}_{avg} }[/math]). The instantaneous velocity often changes as a function of time like position, but over a given time interval, it has an average value. The average velocity is given by the displacement over a time interval divided by the duration of that time interval. (See Derivation of Average Velocity.) If the velocity is constant over time, that velocity is the average velocity.
Kinematic Equations
- [math]\displaystyle{ \vec{r}_f = \vec{r}_i + \vec{v}_{avg} * t }[/math]
- [math]\displaystyle{ \vec{v}_f = \vec{v}_i + \vec{a} * t }[/math] (assumes constant acceleration)
- [math]\displaystyle{ \vec{r}_f = \frac{1}{2} \vec{a} * t^2 + \vec{v}_i * t + \vec{r}_i }[/math]
- [math]\displaystyle{ }[/math]
These equations are not the entirity of kinematics, but they are the useful bits. (there are other eqtns.)
Instead of vector eqtns these can be considered 1D eqtns, which is how youll normally see them. For example:, this eqtn decomposes into these
A Strategy for Solving Kinematics Problems
1. Draw a figure of the given situation
2. Identify the principle that applies to the problem
3. Identify the given information and variables
4. Determine the unknown information need to be found from known information.
6. Substitute known values into the necessary equation and follow the mathematical process necessary.
7. Check your answer and indicate appropriate units.
Examples
Easy
An airplane accelerates down a runway at 3.20 m/s2 for 32.8 s until is finally lifts off the ground. Determine the distance traveled before takeoff.
Solution: d=1720 m
Using the following formula
Medium
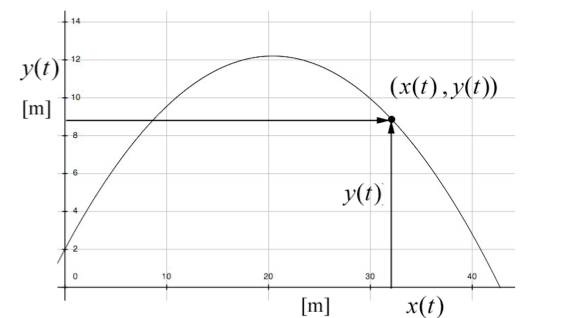
A person throws a stone at an initial angle θ = 45 from the horizontal with an initial speed of v =20m⋅s-1. The point of release of the stone is at a height d=2m above the ground. You may neglect air resistance. a) How long does it take the stone to reach the highest point of its trajectory? b) What was the maximum vertical displacement of the stone? Ignore air resistance.
Solution: Choose the origin on the ground directly underneath the point where the stone is released. We choose upwards for the positive y-direction and along the projection of the path of the stone along the ground for the positive x-direction. Set t = 0 the instant the stone is released. At t = 0 the initial conditions are then x0 = 0 and y0 = d . The initial x- and y-components of the velocity are given by Eqs. (5.1.5) and (5.1.6). At time t the stone has coordinates (x(t), y(t)) . These coordinate functions are shown in the following image:
Difficult
A person is standing on a ladder holding a pail. The person releases the pail from rest at a height h1 above the ground. A second person standing a horizontal distance s2 from the pail aims and throws a ball the instant the pail is released in order to hit the pail. The person releases the ball at a height h2 above the ground, with an initial speed v0 , and at an angle θ0 with respect to the horizontal. You may ignore air resistance. a) Find an expression for the angle θ0 that the person aims the ball in order to hit the pail. b) Find an expression for the height above the ground where the collision occurred as a function of the initial speed of the ball v0 , and the quantities h1 , h2 , and s2 .
Connectedness
Kinematics is at the core of all concepts in physics. Understanding the interaction between forces and how these interactions translate to motion, leaves nearly infinite possibilities. There are thousands of real world examples, such as cars, planes, bow and arrows, and essentially everything that moves.
History
Although humans have questioned the nature of motion for thousands of years, Isaac Newton is credited for the advancement of most topics in kinematics. In 1669, Newton was appointed professor of mathematics at Trinity College. In January 1672, he was elected to the Royal Society, a loose organizations of scientists and intellectuals. Shortly thereafter, he presented a paper detailing his discoveries in optics, and developed a rivalry with the scientist Robert Hooke, who harshly criticized Newton's research. This rivalry would percolate throughout the 1670s, as Newton continued to work out the mathematics of gravity, and would again flare up in the mid 1680s when Newton finally published his work, some of which Hooke felt had been stolen from him.
Newton's research was organized into a three-volume book, the Philosophiae Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy"), known to posterity as the Principia Mathematica. It set forth Newton's three laws of motion, and proceeded to set forth the theory of gravitation, and back it up with rigorous mathematical proofs. Although the theory had many detractors at first, the scientific community would ultimately embrace it, and the Newtonian world-view would dominate physics until the 20th century.
See also
[Vectors] [1]
[Momentum Principle] [2]
[Curving Motion] [3]
[Projectile Motion] [4]
[Newton's Laws and Linear Momentum] [5]
[Net Force] [6]
[Momentum with respect to external Forces][7]
Further reading
Matter and Interactions, 4th Edition
References
http://web.mit.edu/8.01t/www/materials/modules/chapter05.pdf
http://web.mit.edu/8.01t/www/materials/modules/chapter04.pdf
http://www.sparknotes.com/biography/newton/summary.html
http://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations