Superposition Principle
The Superposition Principle states that the net result of multiple vectors acting on a given place and time is equal to the vector sum of each individual vector. For intro physics, this mostly relates to effect that multiple electric or magnetic fields and forces have on a certain location. Claimed by jnmng3 (Fall 2017)
A Mathematical Model
The Superposition Principle is derived from the properities of additivity and homogeneity for linear systems which are defined in terms of a scalar value of a by the following equations:
[math]\displaystyle{ F(x_1 + x_2) = F(x_1) + F(x_2)\quad Additivity }[/math]
[math]\displaystyle{ aF(x) = F(ax)\quad Homogeneity }[/math]
The principle can be applied to any linear system and can be used to find the net result of functions, vectors, vector fields, etc. For the topic of introductory physics, it will mainly apply to vectors and vector fields such as electric forces and fields.
If given a number of vectors passing through a certain point, the resultant vector is given by simply adding all the the vectors at that point. For example, for a number of uniform electric fields passing though a single point, the resulting electric field at that point is given by:
[math]\displaystyle{ \vec{E} = \vec{E}_{1} + \vec{E}_{2} +...+ \vec{E}_{n} = \sum_{i=1}^n\vec{E}_{i} }[/math]
This same concept can be applied to electric forces as well as to magnetic fields and forces. This is more useful when dealing with the effect that multiple point charges have on each other is an area of void of other electric fields. By adding together each of the contributing electric field vectors at a specific point you can figure out the net contribution that all of the present charges have on the overall electric field experienced at said location.
You can calculate the electric field of a single point charge by using the following equation: [math]\displaystyle{ \vec{E} = \frac{1}{4 \pi \epsilon_0}\sum_{i=1}^n\frac{q_i}{r_i^2}\hat{r_i} }[/math]
Examples
When attempting to solve these problems be sure to show all steps in your solution and include diagrams whenever possible.
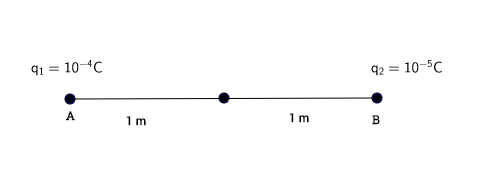
Simple - Two Point Charges and One Dimension
If [math]\displaystyle{ Q_1 }[/math] equals 1e-4 C and [math]\displaystyle{ Q_2 }[/math] equals 1e-5C, what is the net electric field at the midpoint of both charges?
Click for Solution
We know that the distance of each charge to the midpoint is [math]\displaystyle{ 1m }[/math]. Since this value is the magnitude of the distance it will serve as our [math]\displaystyle{ r_i }[/math] value for both of the electric field formulas.
Our [math]\displaystyle{ \hat{r_1} }[/math] value for [math]\displaystyle{ E_1 }[/math] will be [math]\displaystyle{ 1 }[/math] and the [math]\displaystyle{ \hat{r_2} }[/math] value for [math]\displaystyle{ E_2 }[/math] will be [math]\displaystyle{ -1 }[/math], if you use the midpoint as your observation point in the x-direction.
Now that we have all the necessary values to use the electric field formula, we can plug them in.
[math]\displaystyle{ \vec{E_1} = \frac{1}{4 \pi \epsilon_0}\frac{q_1}{r_1^2}\hat{r_1} = (9e9)\frac{1e-4C}{1m^2}(1m) = 9e5\frac{N}{C} }[/math] [math]\displaystyle{ \vec{E_2} = \frac{1}{4 \pi \epsilon_0}\frac{q_2}{r_2^2}\hat{r_2} = (9e9)\frac{1e-5C}{1m^2}(-1m) = -9e4\frac{N}{C} }[/math]
By this point, you have the individual contributions of each charge. To get the net contribution of all the charges, you only need to add them.
[math]\displaystyle{ \vec{E_1}+\vec{E_2}=9e5\frac{N}{C}-9e4\frac{N}{C}= 8.1e5\frac{N}{C} }[/math]
This means that the net electric field will point towards the right with a magnitude of [math]\displaystyle{ 8.1e5\frac{N}{C} }[/math].
Medium - Two Point Charges and Two Dimensions
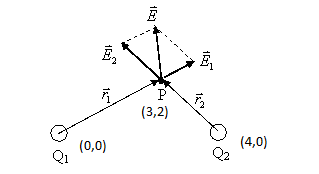If [math]\displaystyle{ Q_1 }[/math] and [math]\displaystyle{ Q_2 }[/math] are positive point charges with a charge of e, what is the net electric field at point P?
Click for Solution
To begin this problem, the first step is to find [math]\displaystyle{ r_1 }[/math] and [math]\displaystyle{ r_2 }[/math], the vectors from the charges to point P as well as their magnitudes:
[math]\displaystyle{ \vec{r_1} = 3\hat{i}+2\hat{j}-(0\hat{i}+0\hat{j})\Rightarrow\vec{r_1} = 3\hat{i}+2\hat{j} }[/math]
[math]\displaystyle{ ||\vec{r_1}|| = \sqrt{3^2 + 2^2} =\sqrt{13} }[/math]
[math]\displaystyle{ \vec{r_2} = 3\hat{i}+2\hat{j}-(4\hat{i}+0\hat{j})\Rightarrow\vec{r_2} = -1\hat{i}+2\hat{j} }[/math]
[math]\displaystyle{ ||\vec{r_2}|| = \sqrt{-1^2 + 2^2} =\sqrt{5} }[/math]
Using these in the equation for an electric field from a point charge, you get:
[math]\displaystyle{ \vec{E_1} = \frac{1}{4 \pi \epsilon_0}\frac{Q_1}{||r_1||^2}\hat{r_1}=\frac{1}{4 \pi \epsilon_0}\frac{e}{13}\lt \frac{3}{\sqrt{13}}\hat{i}+\frac{2}{\sqrt{13}}\hat{j}\gt = \lt 9.21E-11\hat{i}+6.14E-11\hat{j}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_2} = \frac{1}{4 \pi \epsilon_0}\frac{Q_2}{||r_2||^2}\hat{r_2}=\frac{1}{4 \pi \epsilon_0}\frac{e}{5}\lt \frac{-1}{\sqrt{5}}\hat{i}+\frac{2}{\sqrt{5}}\hat{j}\gt = \lt -1.29E-10\hat{i}+2.58E-10\hat{j}\gt }[/math]N/C
Then, simply add the two electric fields together:
[math]\displaystyle{ \vec{E}=\vec{E_1}+\vec{E_2} = \lt -3.69E-11\hat{i}+3.19E-10\hat{j}\gt }[/math]
Difficult - Five Point Charges and Three Dimensions
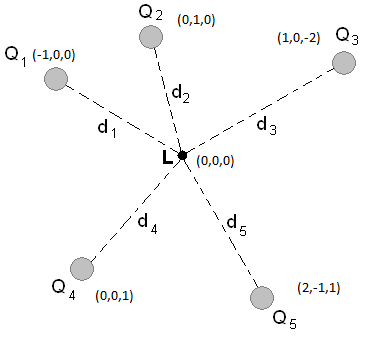If all point charges have a charge of e, what the the net electric field present at point L?
Click for Solution
This problem is similar to the previous example but the now includes the z axis and more points. Since there are 5 points, we'll only focus on one, but work through the whole problem. Again, first each vector and magnitude:
[math]\displaystyle{ \vec{d_5} = 0\hat{i}+0\hat{j}+0\hat{k}-(2\hat{i}-1\hat{j}-1\hat{k})-\Rightarrow\vec{d_5} = -2\hat{i}+1\hat{j}+1\hat{k} }[/math]
[math]\displaystyle{ ||\vec{d_5}|| = \sqrt{(-2)^2 + 1^2 + 1^2} = 2 }[/math]
Do the same for each of the other point charges and plug them into the electric field formula:
[math]\displaystyle{ \vec{E_5} = \frac{1}{4 \pi \epsilon_0}\frac{Q_5}{||d_5||^2}\hat{d_5}=\frac{1}{4 \pi \epsilon_0}\frac{e}{4}\lt \frac{-2}{2}\hat{i}+\frac{1}{2}\hat{j}+\frac{1}{2}\hat{k}\gt = \lt -3.6E-10\hat{i}+1.8E-10\hat{j}+1.8E-10\hat{k}\gt }[/math]N/C
Doing the same steps for the other electric fields and add them all together:
[math]\displaystyle{ \vec{E_1} = \lt 1.44E-9\hat{i}+0\hat{j}+0\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_2} = \lt 0\hat{i}-1.44E-9\hat{j}+0\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_3} = \lt -1.29E-10\hat{i}+0\hat{j}+2.58E-10\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E_4} = \lt 0\hat{i}+0\hat{j}-1.44E-9\hat{k}\gt }[/math]N/C
[math]\displaystyle{ \vec{E} = \vec{E_1}+\vec{E_2}+\vec{E_3}+\vec{E_4}+\vec{E_5}=\lt 9.51E-10\hat{i}-1.26E-9\hat{j}+1.00E-9\hat{k}\gt }[/math]N/C
Connectedness
The superposition principle is critical as you progress to more complicated topics in Physics.
History
The superposition principle was supposedly first stated by Daniel Bernoulli, a famous scientist known for his work in fluid mechanics, statistics, and the Bernoulli Principle. In 1753, he stated that, "The general motion of a vibrating system is given by a superposition of its proper vibrations." This idea was at first rejected by some other popular scientists until it became widely accepted due to the work of Joseph Fourier, a famous scientist known for his work on the Fourier Series, which is used in heat transfer and vibrations, as well as his discovery of the Greenhouse Effect.
See also
Further reading
Books, Articles or other print media on this topic
Superposition of Waves Schrodingers' Cat from a Superposition Point of View
Next Topics
Now that you have a solid understanding of the Superposition Principle, you can move on to these topics:
References
Electric Fields Superposition Principle Daniel Bernoulli Biography Joseph Fourier Biography