Transformation of Energy

Main Idea

Energy Transformation is the process in which energy changes from one form to another. Examples of forms of energy include: Kinetic, Chemical, Thermal, Potential etc. Whenever energy changes its form, there is no net loss of energy (Conservation of Energy). Virtually every process we engage in is accompanied by a transformation of energy. Some common everyday examples of energy transformation include, the chemical energy of coal being converted to thermal energy when burned, or the conversion of electromagnetic energy from the sun into chemical energy in plants.

It is important to account for the efficiency of an energy transformation. Every energy transformation is accompanied by some change in thermal energy. In other words, it is not possible to convert 100 J of chemical energy to 100 J of kinetic energy; some of the chemical energy will be converted to thermal energy. This is usually due to friction.

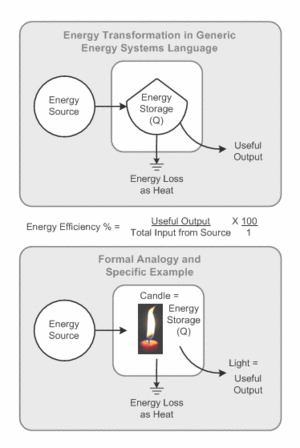
In the figure on the right, there is a candle being burned. When something is burned, the energy stored within the chemical bonds that hold the object together are broken and energy is released. In the figure, the chemical energy of the candle is being converted into both Heat and light. Practically, it would be much more useful if 100% of the chemical energy of the candle was converted into light (the purpose of a candle). If this were the case, either the candle would burn much brighter, or burn longer, since energy is no longer being wasted as Heat. As stated above however, this process is not 100% efficient; Thus, some energy will inevitably be converted into Heat energy.

Mathematical Model

If we assume a system has energy [math]\displaystyle{ E_{0} }[/math] initially, no energy is being converted to work, and no energy energy is being lost or added as Heat, then we can simply say:

[math]\displaystyle{ E_{0} = E_{f} }[/math], where

[math]\displaystyle{ E_{f} = }[/math] the final energy of the system

Note that [math]\displaystyle{ E_{0} }[/math] and [math]\displaystyle{ E _{f} }[/math] don't specify what form the energy takes, merely that their values are equal in Joules when summed. The energy could be transformed in a myriad of ways that are consistent with the above equation.

Computational Model

Insert Computational Model here

The VPython model below demonstrates a space probe orbiting the Earth and Moon. The probe is under the influence of the Earth's gravity and the Moon's gravity. The probe has its own initial velocity.

The graph illustrates the conservation of energy of this system. The yellow curve represents the kinetic energy of the space probe, the blue curve shows the gravitational potential energy of the space probe in orbit, and the green line represents the sum of the kinetic and potential energies. Notice the green line is always the same value... a negative value, meaning the space probe is locked into orbit around the Earth and Moon for now.

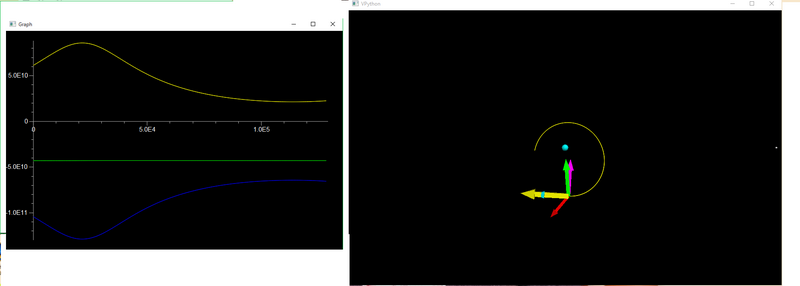
In a more realistic model, some energy would be lost as Heat over time.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A candle has [math]\displaystyle{ 500 \ J }[/math] of chemical energy stored in its wick. After some time, when the entire candle is burned, and all the chemical energy is expended, it is found that the candle heated the surroundings with [math]\displaystyle{ 60 \ J }[/math] of Thermal Energy.

a) Assuming the candle only released Heat and light when it was burned, how much energy must the light have had?

We assume:

[math]\displaystyle{ E_{0} = E_{f} }[/math]

We also know the initial energy was all chemical energy, with an amount of [math]\displaystyle{ 500 \ J }[/math]. We know one of the two components of the final energy also. Therefore, we can solve for the energy of the light:

[math]\displaystyle{ E_{0} = 500 \quad \And \quad E_{f} = E_{light} + 60 }[/math]

[math]\displaystyle{ \therefore E_{light} = E_{0} - 60 = 500 - 60 = 440 \ J }[/math]

Middling

When a person goes fora run, conversions of energy take place to propel the runner forward, to speed them up, and to slow them down. In this example, use the Earth and the person as the system.

a) Write an energy equation that actually depicts the change in energy of the person and Earth system as the person runs down a slope. Assume that the only forms of energy in this equation are gravitational potential, chemical energy, Heat, and kinetic energy.

First, imagine the person is at the top of the slope. They have not begun their run yet. At this point, the person has some gravitational potential energy due to the Earth's gravity and some potential chemical energy. Then, the person pushes off the ground, using chemical energy to make the push, and thus converting it to kinetic energy and Heat. Also, this movement allows the person to head down the slope, decreasing their gravitational potential energy, which is converted into more kinetic energy and Heat (from the friction of the person and the air). Thus, we imagine a conservation of energy equation for this person would be something like:

[math]\displaystyle{ E_{chemical_{0}} + E_{gravity_{0}} = E_{chemical_{f}} + E_{gravity_{f}} + E_{kinetic} + E_{thermal} }[/math]

This equality states the person's energy is initially comprised of the person's chemical energy and gravitational potential energy, and this initial energy is equal to the leftover chemical energy energy, the leftover gravitational potential energy, the gained kinetic energy from the chemical and gravitational potential, and the energy lost in this process as Heat. It is worth noting this can be rewritten as:

[math]\displaystyle{ (E_{chemical_{0}} - E_{chemical_{f}}) + (E_{gravity_{0}} - E_{gravity_{f}}) = E_{kinetic} + E_{thermal} }[/math]

[math]\displaystyle{ -( \Delta E_{chemical} + \Delta E_{gravity}) = E_{kinetic} + E_{thermal} }[/math]

[math]\displaystyle{ \Delta E_{chemical} + \Delta E_{gravity} + E_{kinetic} + E_{thermal} = 0 }[/math]

More succinctly:

[math]\displaystyle{ \Delta U_{potential} + E_{kinetic} + Q = 0 }[/math]

This is a form of the Energy Principle, where the initial kinetic energy of the system is [math]\displaystyle{ 0 }[/math].

Difficult

A stirring water heater is built to heat water. We will imagine a water heater where the water is heated by a stirrer, that does work on the water/supplies kinetic energy to the water.

[math]\displaystyle{ 20 \ kg }[/math] of water at [math]\displaystyle{ 25°C }[/math] is heated and forced to evaporate at [math]\displaystyle{ 100°C }[/math] every second.

Assume the specific heat capacity of water varies little within the given Temperature range, this process takes place at a pressure of 1 atmosphere, the efficiency of the stirrer in applying its kinetic energy to warming the water is [math]\displaystyle{ 70% }[/math], the process is continuous, with 0 accumulation, no other Heat is added or lost by the water heater, and the closed system keeps a constant volume and pressure.

a) How much energy must the stirrer transfer to the water per second to achieve this? Assume the process takes place in an adiabatic closed system with a constant volume and pressure.

We must first find the total energy needed to vaporize the water. This comes in two parts:

The Thermal Energy that must be added to the water to heat it from [math]\displaystyle{ 25°C }[/math] to [math]\displaystyle{ 100°C }[/math]
The Thermal Energy that must be added to the water to vaporize it once it is at [math]\displaystyle{ 100°C }[/math]

We will tackle part 1 first by using:

[math]\displaystyle{ \Delta Q = m C \Delta T }[/math]

We know the mass of the water, the specific heat of water, and the Temperature change we are examining. Thus, the change in Thermal Energy will be:

[math]\displaystyle{ \Delta Q = 20 \ (kg) \times 4.18 \left(\frac{kJ}{kg \cdot °C}\right) \times (100 - 25) \ (°C) = 20 \times 4.18 \times 75 = 6,270 \ kJ }[/math]

Now, to find the energy needed to vaporize the water, we must use the Heat of Vaporization of water [math]\displaystyle{ (V_{w}) }[/math]:

[math]\displaystyle{ V_{w} = 2,257 \ \left(\frac{kJ}{kg}\right) }[/math]

Multiplying the Heat of Vaporization by the mass of the water will give the necessary Heat:

[math]\displaystyle{ Q_{vaporize} = mV_{w} = 20 \ (kg) \times 2,257 \ \left(\frac{kJ}{kg}\right) = 45,140 \ kJ }[/math]

The total energy that must be added to vaporize the [math]\displaystyle{ 20 \ kg }[/math] of water is:

[math]\displaystyle{ Q_{total} = \Delta Q + Q_{vaporize} = 6,270 + 45,140 = 51,410 \ kJ }[/math]

This energy is equal to the amount of Thermal Energy that must be added by the stirring, but since the stirrer is only working at [math]\displaystyle{ 70% }[/math] efficiency, the kinetic energy of the stirrer will be greater than this. In fact, it will be greater than the needed Thermal Energy according to:

[math]\displaystyle{ 0.7KE_{stirrer} = Q_{total} }[/math]

or:

[math]\displaystyle{ KE_{stirrer} = \frac{Q_{total}}{0.7} = 73,442.86 \ kJ }[/math]

The energy the stirrer must produce every second to heat the water accordingly is [math]\displaystyle{ 73,442.86 \ kJ }[/math], or [math]\displaystyle{ 73,442.86 \ kW }[/math].

Connectedness

I am currently very interested in oil refinery and as a chemical engineer, I hope to some day work in this sector. Oil is probably one of the most converted energy sources in the world. The whole point of refinery is to extract the maximum amount of usable energy from the chemical bonds of oil. This is accomplished through the use of changing parameters such as pressure, temperature, volume etc. This is directly applicable to energy transformation since the whole point of this process is to use what we know about the properties of oil and make energy efficiency as close to 100% as possible.

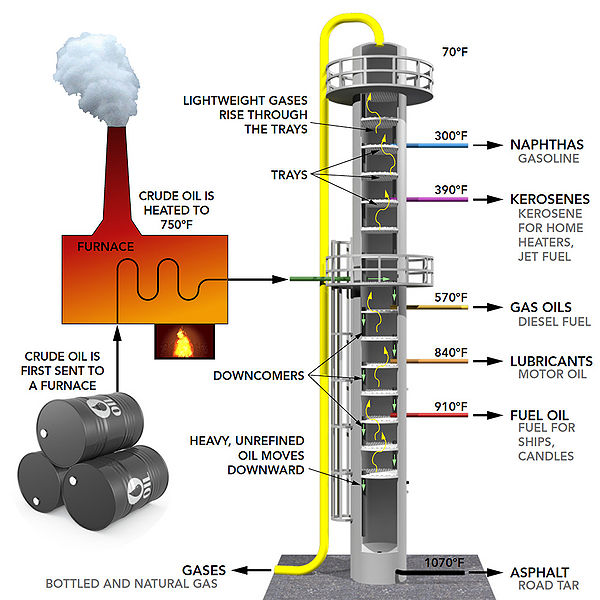
History

Energy has been converted through many forms since the beginning of time with the Big Bang, and the formation of the first stars. Humans themselves are constantly converting chemical energy into kinetic energy as we go about our daily lives. It can be argued that transformation of energy really began happening on a large scale with the entrance of the Industrial Revolution in the late 1700's. At this point in time, the chemical energy in coal was being converted to thermal energy to heat up water, which was then used to turn turbines and generate usable energy. Today, energy conversion is all around us. Perhaps the most common form of energy transformation is electrical energy. A myriad of appliances exist that can convert electrical energy into any form of energy depending on what type of energy is required that situation.

Transformation of Energy

Contents

Main Idea

Mathematical Model

Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu