Quantum Theory

Claimed by Nathan Donagi Fall 24

https://www.glowscript.org/#/user/Nathan_Donagi/folder/MyPrograms/program/HydrogenAtom

Visualization of the Bohr Model of the atom.

The Main Idea

Quantum theory is the accepted modern explanation of the observed behaviors of matter based upon atomic energy and particle interactions. After many notable physicists had hypothesized and disproved various theories to describe the structure of the atom, scientists arrived at the Bohr Model, which currently has the most support from other work and theories from quantum mechanics. After the Rutherford's Gold Foil Experiment, the idea came about that the atom actually exists as many particles held together or near each other by electromagnetic force, which is the attraction or repulsion of charged particles, or the strong force, which holds protons and neutrons together at the nucleus of an atom, and that between these particles there is nothing but empty space. Why these particles stay together in certain configurations and their reactions to incidence with energy or other other particles is explained by quantum physics. The atomic and subatomic characterizations made possible by quantum mechanics differentiate it from classical mechanics. For example, a quantum description of the universe indicates that all objects exhibit a Wave-Particle Duality, meaning all entities express the characteristics of both waves an particles. Additionally, as opposed to classical physics, the elements of momentum, angular momentum, and energy are quantized. In a bound system, they are constrained to discrete values.

History

The theory and all of its applications, much like any other scientific development of the 20th century, comes from contributions of multiple notable scientists over the course of many years. Initially, Newtonian Laws dominated physics, but the atom was represented by the plum pudding model, which developed after the discovery of the electron and the idea that atom must be made from more particles than previously suspected. None of the leading theories at the time, though, could explain electric discharges or the phenomenon of black lines appearing in the spectra from light passed through various materials. Some scientists were unsure of whether electrons existed as particles or if the electrons themselves were the energy and radiation observed from interactions with atoms. One of the earliest elements that lead to the current model was Max Planck's idea that energy could be quantified or defined by smaller units, which he called "quanta". Later, Albert Einstein applied Planck's work to radiation via what is called the photoelectric effect, where he determined that the results of electron particle interaction with incident radiation, not just energy, depended specifically upon the frequency of the radiation. Niels Bohr determined his model of atomic structure in 1913; rejecting that idea that electrons orbiting the nucleus eventually radiate energy and fall into the nucleus, he proposed that electrons were held in fixed orbits by electromagnetic forces and that they could shift to other orbits, or other energy levels, by absorption or emission of energy. Werner Heisenberg also suggested that electrons simply could not possibly be defined by an exact location or momentum by physicists, not without applying some radiation incident to the electron and measuring the disturbance of the system in effect- this idea known as the uncertainty principle. All of these ideas come together to form our current understanding of quantum physics, which greatly impacts the practice of modern physics.

1900 - Max Planck proposed Planck's radiation law to explain the radiation emission of blackbody. He also proposed the quantization of photons, which is now known as the equation e=h ν。 Therefore, quantum mechanics was born.

1902 - Hendrick Lorentz explained the Zeeman effect through Lorent's ether theory.

1905 - Albert Einstein explained the photoelectric effect. He regarded light as particles, so he advocated Newton's particle theory. He also introduced the special theory of relativity to the world.

1909 - Ernst Rutherford α The concept of atomic nucleus is proposed in the X-ray scattering experiment (also known as the gold foil experiment).

1909 - Geoffrey Taylor proved the formation of single photon interference mode, which rekindled the Newton Huygens debate for more than two centuries.

1913 - Johannes stark discovered the Stark effect, an electric field phenomenon similar to the Zeeman effect.

1913 - Niels Bohr introduced his atomic model and put forward the theory of quantifying atomic radius.

1915 - Einstein proposed general relativity and Einstein's field equations (see quantum field theory).

1916 - Einstein theoretically pointed out that Planck's energy quantum has particle like momentum.

1916 -- Arnold Sommerfeld proposed the concept of atomic sub shell, which extended Bohr's atomic theory.

1918 - Ernst Rutherford discovered protons (and coined the word) in atoms.

1921 - Theodore Kaluza published Kaluza theory (the first theory related to quantum field theory).

After the previous discoveries and the sudden prosperity of scientific discoveries led by quantum and relativity, the formalization of quantum mechanics, a new field of physics, has become clear. Bohr, Heisenberg and Schrodinger began to develop this formalization in the 1920s, and soon Max Born, Paul Dirac and John von Neumann joined the ranks.

1922 - Arthur Compton discovered the Compton effect.

1922 - Otto stern and Walter graher conducted the stern graher experiment, which proved the quantification of spin.

1923 - Louis de Broglie assumed wave particle duality and de Broglie wavelength λ= h/mv。

1924 - Wolfgang Pauli explained the fine structure of spectral lines with the concept of internal angular momentum of electrons.

1925 - George Ulenbeck and Samuel goodschmidt proposed the existence of electron spin.

In 1925, Heisenberg, born and Pascal Jordan proposed the matrix mechanics expression of quantum physics.

1925 - Frederick hund theoretically proposed the principle of maximum multiplicity in atoms, which is now known as the hund rule.

1926 - Erwin Schrodinger proposed the Schrodinger wave equation, which is the most important equation in quantum mechanics.

1926 - Oscar Klein explains the Kaluza hypothesis (one of the earliest ideas about quantum gravity) by integrating the quantum mechanics created by Heisenberg and Schrodinger.

1927 - Werner Heisenberg published an article introducing Heisenberg's uncertainty principle: Δ p· Δ x≥h/4π。

1927 - Solvay conference, proposed the Copenhagen interpretation of quantum mechanics.

1928 - Paul Dirac established the Dirac equation of quantum mechanics.

1929 - Oscar Klein predicted the Klein paradox, the quantum tunneling effect.

1930 - Paul Dirac postulated positrons.

1930 - Paul Dirac proposed hole theory (also known as Dirac sea model).

1932 - John von Neumann described the mathematical basis of quantum mechanics from the perspective of Hermite operators and linear algebra.

Mathematical Application

From the development of the quantum theory, we obtain fundamental equations and others which are very useful in introductory physics problems.

As Einstein determined, the incident energy that may be absorbed or emitted from electrons (or any particle for this case) depends on the frequency of the radiation:

[math]\displaystyle{ {E} = {hν} }[/math] in units of joules (J)

where Planck's constant (h) = 64985 Joules/Coloumb and ν(nu) is the frequency of the radiation, which is also [math]\displaystyle{ {ν} = {\frac{c}{λ}} }[/math]

The radius of an electron's orbit may be determined from:

[math]\displaystyle{ {r} = {\frac{Nλ}{2π}} }[/math] or [math]\displaystyle{ {r} = {\frac{Nh}{2π|\vec{p}|}} }[/math] where N is the energy level in which the electron is orbiting and λ is the wavelength

From the derivation of the orbit's radius, we can find the angular momentum of the electron:

[math]\displaystyle{ {\vec{L}} = {\vec{r}x\vec{p}} = {\frac{Nh}{2π}} }[/math]

The centripetal force holding the electron in circular motion is the electromagnetic force produce from the positive charges of the protons in the nucleus and negative charges of the electrons:

[math]\displaystyle{ {F_{perpendicular}} = {\frac{mv^2}{r}} }[/math] [math]\displaystyle{ {F_{electromagnetic}} = {\frac{1}{4πε_0}\frac{q_e^2}{r^2}} }[/math]

from this radius of the orbit may also be found with [math]\displaystyle{ {r} = {\frac{N^2h^2}{ke^24π^2m}} }[/math] where [math]\displaystyle{ {k} = {\frac{1}{4πε_0}} }[/math]

The total energy of an electron, specifically in the case of the hydrogen atom:

[math]\displaystyle{ {E} = {\frac{-13.6}{N^2}} }[/math] in units of electron volts (eV) where [math]\displaystyle{ {1eV} = {1.6x10^{-19} J} }[/math]

Other energy calculations for an electron orbiting a hydrogen nucleus:

Potential Energy [math]\displaystyle{ {U} = {{-}\frac{1}{4πε_0}\frac{q_e^2}{r}} }[/math] may also be found with [math]\displaystyle{ {U} = {\frac{-27.2}{N^2}} }[/math]

Kinetic Energy [math]\displaystyle{ {K} = {\frac{1}{2}\frac{kq_e^2}{r}} }[/math]

Total Energy [math]\displaystyle{ {E_T} = {{U}+{K}} = {{U} + {\frac{-U}{2}}} = {\frac{U}{2}} }[/math]

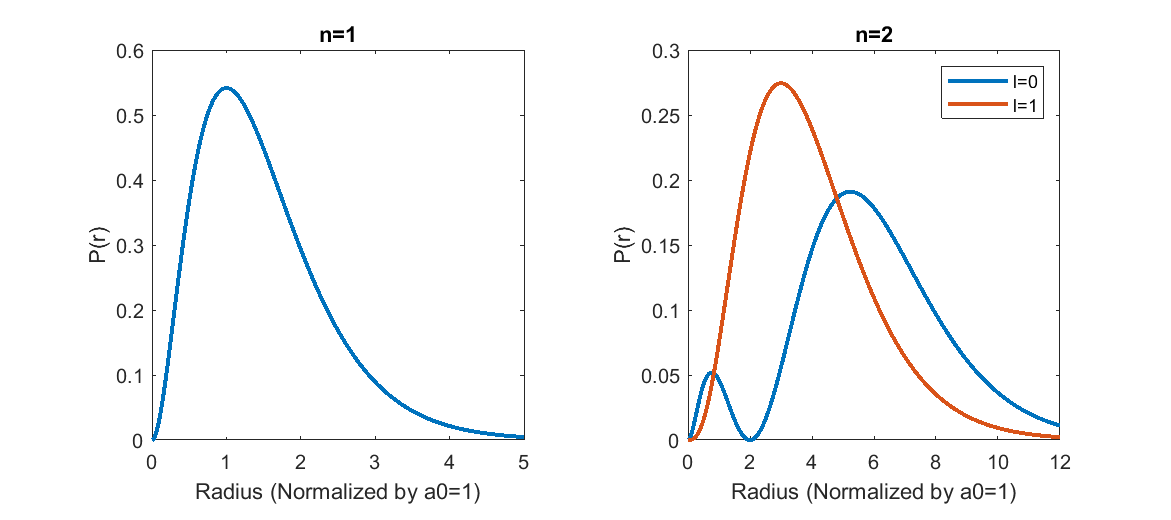
Several indices evolve out of the Schrödinger equation solutions for the three-dimensional hydrogen atom. These parameters include the principle quantum number [math]\displaystyle{ n }[/math], where [math]\displaystyle{ n=1,2,3... }[/math], the angular momentum quantum number [math]\displaystyle{ l }[/math], where [math]\displaystyle{ l=0,1,2,...n-1 }[/math], and the magnetic quantum number [math]\displaystyle{ m_l }[/math], where [math]\displaystyle{ m_l=0,±1,±2,...,±l }[/math].

A complete spatial description of electrons within the hydrogen atom is given for the solution to the three-dimensional Schrödinger Equation. For spherical polar coordinates, the solution is separable. The radial function ([math]\displaystyle{ R }[/math]), polar function ([math]\displaystyle{ \Theta }[/math]), and azimuthal function ([math]\displaystyle{ \Phi }[/math]) can be factored as:

[math]\displaystyle{ {\Psi(r,\theta,\phi)} = R(r)\Theta(\theta)\Phi(\phi) }[/math]

The first several solutions to the wavefunction of the hydrogen atom are given below.

The probability of an electron existing at a given radius from the hydrogen atom can be expressed as:

[math]\displaystyle{ P(r)=|\Psi(r,\theta,\phi)|^2dV }[/math], which simplifies to [math]\displaystyle{ P(r)=r^2|R_n,_l(r)|^2 }[/math]

Integrating over this probability function from one radius to another will provide the probability of an electron appearing in that particular range.

Examples

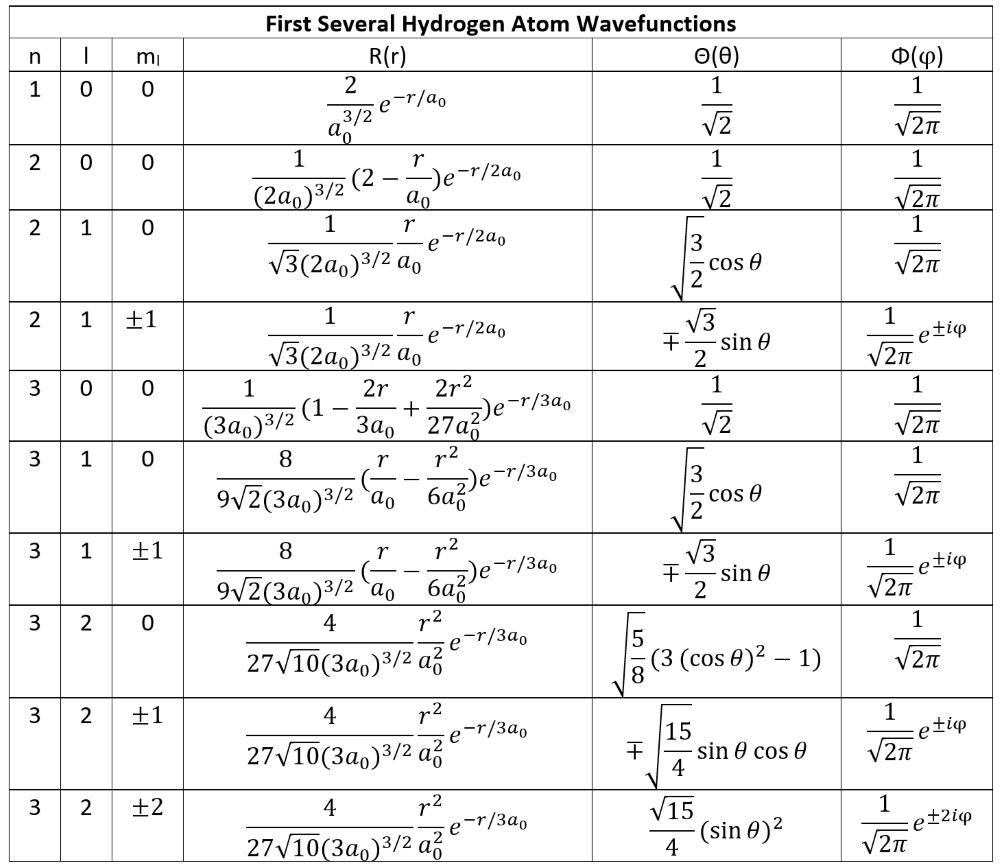
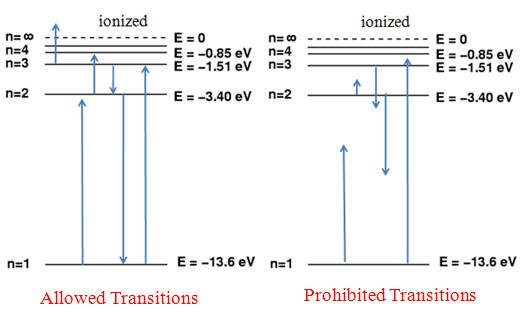
Excitation of Hydrogen's Electron

Adsorption and Emission of Energy by Electrons.

If energy is imparted on the orbiting electron of a hydrogen atom, the resulting transfer of energy will raise the energy level of the electron. Since the electron's only applying force prior to the incident energy is the electromagnetic force holding it to the atom, its total energy is negative. Adding energy increases the value of its total energy by an amount equal to that energy adsorbed; furthermore, the only amounts of energy that the electron will take in are those exactly equal to the amount required to completely move it one or more energy levels (meaning it cannot orbit between energy levels, as that event is not stable and the particle will shift immediately to change it). Although electrons are known to move up in energy levels (excited states), it will always release the energy almost immediately after in order to transition back down to a lower energy state (the lowest level known as the ground state E1) where the atom will be more stable and balanced. Applying the full energy that binds the electron to the atom will be a resulting level greater than the extent of the nucleus' attractive force, and the electron will be released from orbit, effectively ionizing the atom.

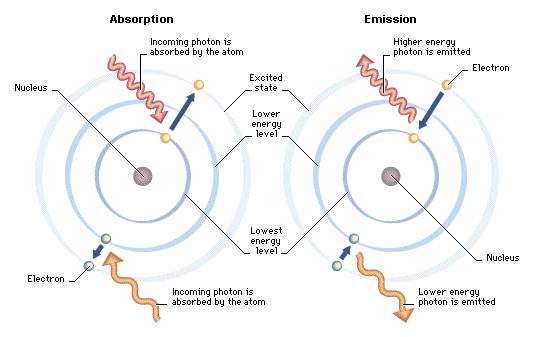
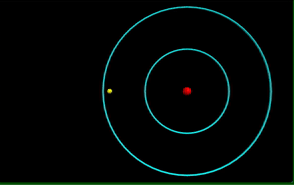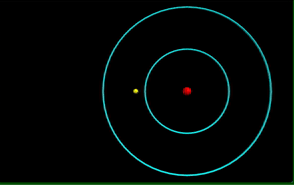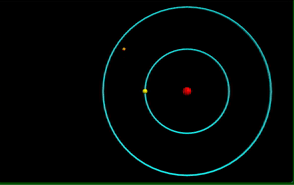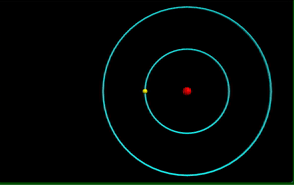
Computational model of photon emission from a hydrogen atom.

Graph illustrating the ground and excited states achieved by electrons with applied radiation. As well, an illustration of how only exact quantities of energy applied have effective results.

Important to note: If another particle such as an electron collides with the electron of our system, then the amount of energy imparted to our system's electron may any amount required to move up by one or more energy level up to a maximum equal to the total kinetic energy of the colliding electron. If our system's electron gains energy from radiation, such as a photon, then the electron will absorb it completely; therefore, this instance may only occur if the total energy of the photon is equal to the amount required to move up by one or more energy levels.

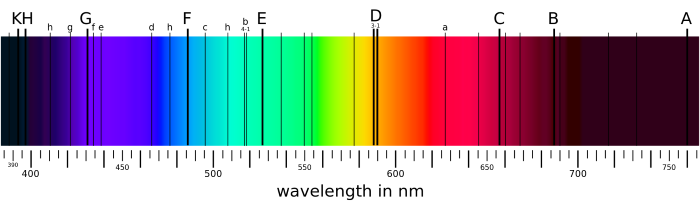
Multiple elements and their corresponding black line regions of the spectrum at wavelengths which their electrons absorb photons.

Applying visible radiation to pure samples allowed scientists to determine which wavelengths of the visible spectrum are absorbed by certain materials and which wavelengths are a reflected. This procedure explained both why we perceive certain colors for specific elements and the black lines of the spectra emitted from samples; the black lines are the locations in the spectra of photons with wavelengths absorbed by the electrons of the atom since they have the exact amount of energy needed to transition to another energy level. All of the other wavelengths are sent away from the atom and eventually taken in by receptors in our eyes.

Probability densities for the first couple levels of the hydrogen atom.

The maximally probable location of the election at the lowest level is at the Bohr Radius [math]\displaystyle{ a_0 }[/math]. As the electron level increases, the average distance of the electron from the center of the atom increases. For an increase from the first to the second electron level, there is also an increase in the number of maxima. The first maxima appears at [math]\displaystyle{ r=n^2a_0 }[/math], and occurs for each [math]\displaystyle{ n }[/math] where [math]\displaystyle{ l=n-1 }[/math]. It is also notable that the probability density [math]\displaystyle{ |\Psi|^2 }[/math] may not equal zero at [math]\displaystyle{ r=0 }[/math], but the [math]\displaystyle{ r^2 }[/math] factor guarantees that [math]\displaystyle{ P(r)=0 }[/math] at that location.

Intro to Spin(Electrons)

what is spin of electrons in Quantum Mechanics

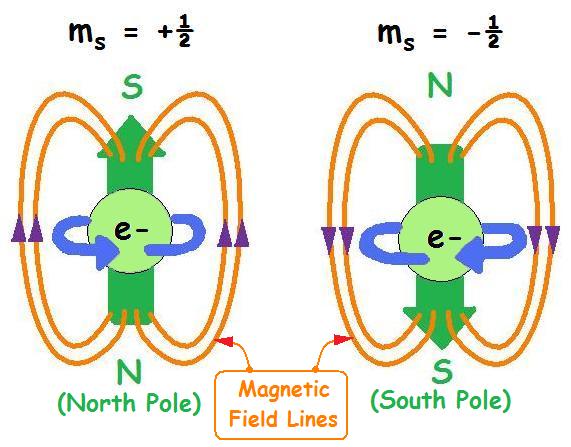
One of the basic properties of electrons. The abbreviation of electron intrinsic motion or quantum number of electron intrinsic motion. In 1925, inspired by the Pauli exclusion principle, G.E. Ulenbeck and S.A. guzmitt analyzed some experimental results of atomic spectroscopy and proposed that electrons have intrinsic motion - spin, and have spin magnetic moments associated with electron spin. This can explain the fine structure of atomic spectra and the abnormal Zeeman effect. Where electron spin s= 1/2. In 1928, p.a.m. Dirac proposed the relativistic wave equation of electrons, which naturally includes electron spin and spin magnetic moment. Electron spin is a quantum effect, which cannot be understood classically. If we regard electron spin as rotation around an axis, we will get a result that is contradictory to relativity.

Spin quantum numbers describe the angular momentum of electrons. The electron rotates around the axis and has both angular momentum and orbital angular momentum. And because one orbit can only hold two electrons, one electron is positive 1/2 and the other is -1/2

Connectedness

Quantum physics is considered one of the fundamental concepts of modern physics studies, promoting the establishment of fields of study such as elementary particles, condensed matter, superconductivity, nuclear physics, chemistry, and other applications of radiation to matter. Understanding atomic structure and behavior with radiation is an important concept for studying most of the real world. Especially in fields of physical chemistry and even analytical chemistry are further developed by innovations in theory and thinking. From this understanding, instrumental observations of other parts of the solar system may be analyzed more effectively to determine chemical make-up and behavior on other bodies. Applications of absorbance and transmittance are useful in determining chemical composition, concentration, or effective uses of synthesized compounds.

Quantum Theory

Contents

Claimed by Nathan Donagi Fall 24

The Main Idea

History

Mathematical Application

Examples

Excitation of Hydrogen's Electron

Intro to Spin(Electrons)

Connectedness

See also

Further reading

External links

References

Navigation menu