Motional Emf using Faraday's Law
Claimed by Aditya Bhairampally, Fall 2025
The Main Idea
We have previously shown that an electromotive force (emf) can be generated by changing the magnetic flux (see week 10, Motional EMF). The emf generated is directly proportional to the negative rate of change of the magnetic flux. The negative sign is a representative of the conservation of energy or Lenz's Law. Basically the magnetic field created by the induced current (induced by the external magnetic field) needs to oppose the external magnetic field otherwise new energy is created which breaks the law of conservation of energy. In the examples provided in the section "Motional Emf" the magnetic flux is changed by changing the areas of the loops. But as per the Magnetic Flux equations, the flux can also be changed by varying the magnitude and/or direction of the applied magnetic field. So what happens when the magnetic field changes and not the area? This is were Faraday comes in. He discovered through his experiments that the Magnetic flux equation is valid no matter how the flux is changing which allowed him to relate the electric and magnetic fields in a new law. Which is named after him as Faraday's Law but Maxwell also wrote down the differential form of the same law before him.
When a wire moves through an area with applied magnetic field with velocity [math]\displaystyle{ {\vec{v}} }[/math], a current begins to flow across it. The wire moving means that the electrons inside the wire are also moving with the same velocity [math]\displaystyle{ {\vec{v}} }[/math] as the wire. As you remember from previous sections that a charge moving in an external magnetic field experience a magnetic force. This force then pushes the electrons to a direction determined by the cross product of the velocity of the electrons [math]\displaystyle{ {\vec{v}} }[/math] and the magnetic field [math]\displaystyle{ {\vec{B}} }[/math] times the charge of an electron which is [math]\displaystyle{ {-e} }[/math]. This makes the electrons accumulate on one side of the wire, thus polarizing the wire. This polarization gives rise to an electric field inside the wire which creates a force on the electrons opposite to the magnetic force on the electrons, hence, in steady the electrons in a wire experience zero net force. Now imagine the ends of the wire are connected to a load. This allows the accumulated electrons to flow around the loop. This means that the electric field decreases hence the net force is doesn't go to zero in steady-state which means a current is induced in the loop and hence and electromotive force (emf).
Originally, we calculated the motional emf in a moving bar by using the equation [math]\displaystyle{ {\frac{q(\vec{v} \times \vec{B})L}{q}} }[/math] where [math]\displaystyle{ {\vec{v}} }[/math] is the velocity of the bar and [math]\displaystyle{ {L} }[/math] is the bar length. However, writing an equation for emf in terms of magnetic flux can yield simpler calculations. Motional emf has a differential relationship to magnetic flux. If an enclosed magnetic field remains constant but the loop changes shape or orientation, the resulting change in the area leads to a change in magnetic flux. For an in-depth conceptual breakdown of motional emf see Motional Emf, for more details on other applications of Faraday's law see Faraday's Law.
A Mathematical Model
Motional emf results when the area enclosing a constant magnetic field changes. Let's observe a specific scenario in which a bar of length L slides along two frictionless bars. We can observe the change in area over a short time as [math]\displaystyle{ \Delta{A} = L\Delta{x} = Lv\Delta{t} }[/math]. We already know that magnetic flux is defined by the formula: [math]\displaystyle{ \Phi_m = \int\! \vec{B} \cdot\vec{n}dA }[/math]. In the case that v is perpendicular to B, we combine these to get: [math]\displaystyle{ \frac{\Delta{\Phi_m}}{\Delta{t}} = BLv }[/math].
Emf is said to be the work done per unit charge: [math]\displaystyle{ emf = \frac{FL}{q} = \frac{qvBL}{q} = vBL }[/math] (again, we are assuming v is perpendicular to B).
Comparing the above two formulas, we can clearly see that [math]\displaystyle{ |{emf}| = |\frac{d\Phi_m}{dt}| }[/math]. This is exactly what Faraday's Law tells us!
where [math]\displaystyle{ \vec{E} }[/math] is the Non-Coulomb electric field along the path, [math]\displaystyle{ l }[/math] is the length of the path you're integrating on, [math]\displaystyle{ \vec{B} }[/math] is the magnetic field inside the area enclosed, and [math]\displaystyle{ \vec{n} }[/math] is the unit vector perpendicular to area A.
A Computational Model
Bar sliding along two frictionless rods
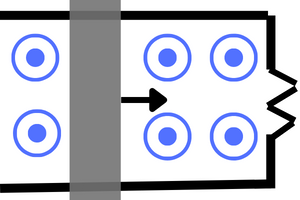
The following simulation animates a bar sliding along two frictionless rods that are connected to a resistor of resistance R. As the bar moves along the area of the loop it creates with the two rods and the resistor increases and decreases depending on the direction of its velocity.
Click here to view the simulation for inducing emf by varying the area of the loop whilst keeping the applied magnetic field constant.
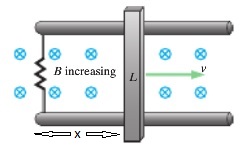
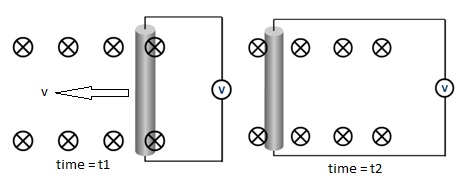
In the image shown to the left, a bar of length [math]\displaystyle{ L }[/math] is moving along two other bars from right to left. The blue circles containing "x"s represent a magnetic field directed into the page. As the bar moves to the right, the system encloses a greater amount of magnetic field.
To explain this concept more clearly, take a look at the figures above. This image shows a bar moving in a magnetic field at two different times. In the first picture, at time [math]\displaystyle{ t_1 }[/math], the system encircles half of two individual magnetic field circles. However, in the second picture taken at time [math]\displaystyle{ t_2 }[/math], the system now encircles 6 full magnetic field circles. Of course, this explanation isn't using technical terms, but the point still stands: the enclosed magnetic field is increasing as time increases.
Returning to the scenario in the first image, because the magnetic field is not constant, we can use Faraday's Law to solve for the motional emf.
As stated above, the formula is as follows:
First, integrate the integral with respect to the area of the rectangle enclosed.
We have the dimensions of the bar in variables: length [math]\displaystyle{ L }[/math] and width [math]\displaystyle{ x }[/math]. Substitute these values for the area, [math]\displaystyle{ A }[/math]
Now that we have this formula, we have to figure out how to take its derivative with respect to [math]\displaystyle{ t }[/math]. Which of the magnitudes of these values is changing?
- The magnitude of the magnetic field is constant. (More "circles" are added as time increases, but the magnitude of each "circle" does not change.
- The magnitude of the normal vector is constant.
- The length, [math]\displaystyle{ L }[/math], of the bar is constant.
- The width of the surface enclosed, [math]\displaystyle{ x }[/math], changes.
As a result, the formula now becomes:
In this case, [math]\displaystyle{ \frac{dx}{dt} = \vec{v} }[/math] because [math]\displaystyle{ x }[/math] is a function of time, where [math]\displaystyle{ \vec{v} }[/math] is the velocity of the moving bar. Substituting that in, we get:
Plugging in these values, we can solve for the motional emf of the bar.
Because the magnetic field is changing with time, however, there is also an induced current flowing through the circuit. We can find the direction of the current using the right-hand rule. To do this, we can use 2 different methods:
- 1. We can use the equation [math]\displaystyle{ \vec{F} = q\vec{v} \times \vec{B} }[/math], where [math]\displaystyle{ \vec{F} }[/math] is the force on the bar, and [math]\displaystyle{ \vec{v} }[/math] is the velocity of the bar. Using the right-hand rule, we can point our fingers in the direction of the velocity of the bar and curl them in the direction of the magnetic field. The direction that our thumb points is the direction of the force on a positive charge. In this case, [math]\displaystyle{ \vec{F} }[/math] points upward, so the positive charges in the bar will move to the top, causing it to polarize with positive charges at the top and negative charges at the bottom. We can now visualize the bar as a battery that causes a current [math]\displaystyle{ I }[/math] to run out of the positive end. In this case, since the bar is polarized with the positive charges at the top, the current will flow out of the top of the bar and continue around the circuit.
- 2. We can use the negative direction of the change in magnetic field, [math]\displaystyle{ -\frac{dB}{dt} }[/math] to find the direction of the current. To do this, make a diagram comparing the magnitude of the magnetic field enclosed at time [math]\displaystyle{ t_1 }[/math] and at time [math]\displaystyle{ t_2 }[/math]. Then, draw an arrow representing the direction of change of the magnetic field. Now, flip the arrow to take the negative of that vector's direction. Using the right-hand rule, point your thumb in the direction of [math]\displaystyle{ -\frac{dB}{dt} }[/math], and the curl of your fingers will give you the direction of the induced current, [math]\displaystyle{ I }[/math].
If the magnetic field is NOT constant, meaning it changes with time, the derivative [math]\displaystyle{ \frac{d}{dt} }[/math] will be distributed to both [math]\displaystyle{ \vec{B} }[/math] and [math]\displaystyle{ x }[/math] in the formula. In this case, we must use the product rule to be able to set up the equation and continue solving for [math]\displaystyle{ emf }[/math].
The B (dA/dt) can be replaced by BLv.
The first term, [math]\displaystyle{ (\frac{d}{dt}\vec{B})A }[/math], represents Faraday's law and is nonzero of there is a varying magnetic field.
The second term, [math]\displaystyle{ B(\frac{d}{dt}A) }[/math], represents motional emf and is nonzero if there is a change in the amount of enclosed area.
Constant velocity rod simulation
The following simulation shows motional EMF in a conducting rod that moves at a constant velocity along two parallel rails in the presence of a uniform magnetic field. As the rod moved through the magnetic field, the charge carriers inside it experience a magnetic force given by [math]\displaystyle{ \vec{F} = q \, \vec{v} \times \vec{B} }[/math] which drives the positive and negative charges toward opposite ends of the rod. This separation of charge produces an electric field inside the rod and results in an induced EMF.
For a rod of length L moving with speed [math]\displaystyle{ \mathbf{\vec{v}} }[/math] through a magnetic field of magnitude B, the induced EMF is [math]\displaystyle{ E = B L \, \mathbf{v} }[/math].
In the simulation, the rod moves with constant speed and the magnetic field is shown by arrows directed into the screen. Since B, L and [math]\displaystyle{ \mathbf{\vec{v}} }[/math] are constant, the induced EMF remains constant as well. The value of the EMF is displayed above the rod and a graph of EMF VS time is shown below the simulation.
Click here to view the simulation: https://trinket.io/glowscript/d47499403833?outputOnly=true
Accelerating rod simulation
The following simulation shows the motional EMF in a conducting rod that accelerates along two parallel rails within a uniform magnetic field. As the rod moves, the charges inside experience a magnetic force given by [math]\displaystyle{ \vec{F} = q \, \vec{v} \times \vec{B} }[/math], where [math]\displaystyle{ \mathbf{\vec{v}} }[/math] is the instantaneous velocity of the rod. This force separates positive and negative charges, creating an induced electric field along the rod, which produces an EMF.
Because the rod is accelerating, its velocity [math]\displaystyle{ v = at }[/math] increases over time causing the motional EMF which is calculated as [math]\displaystyle{ E = B L \, \mathbf{v} }[/math] to increase linearly as the rod moves.
This simulation shows how Faraday's law of induction applies when a conductor moves with changing velocity through a magnetic field.
Click here for the simulation: https://trinket.io/glowscript/142c6680f252?outputOnly=true
Python Visual
Here is a visual to use in GlowScript that shows the polarization of a metal bar as it moves toward a capacitor
First, we create the positive and negative sides of our capacitor:
newCapacitorNegative = box(pos=vec(2, 0, 0), size = vec(1, 3, 0), color = color.white) newCapacitorPositive = box(pos=vec(-2, 0, 0), size = vec(1, 3, 0), color = color.white)
Then, we write code to show our wire
wireVertleft = box(pos = vec(-2, -2.5, 0), size = vec(.25, 2, 0), color = color.yellow) wireVertRight = box(pos = vec(2, -2.5, 0), size = vec(.25, 2, 0), color = color.yellow) wireHorizontal = box(pos = vec(0, -3.5, 0), size = vec(4.25, .25, 0), color = color.yellow)
Next, we initialize our battery, and write a loop to connect the battery to our wire
ybat = -5 battery = box(pos = vec(0, -5, 0), size = vec(.7, .5, 0), color = color.green)
while(ybat < -3.5):
rate(10)
ybat = ybat + .2
battery.pos = vector(0, ybat, 0)
print("Battery is connected!")
Then, we run a loop to show the movement of the current through the battery, wire, and capacitor, and charge our capacitor
count = -1
current = arrow(pos = vec(0, -3.5, 0), color = color.blue)
while(count < 2):
current.pos = vec(0, -3.5, 0)
xvelocity = vec(.1, 0, 0)
dt = 1
while(dt < 5):
rate(15)
current.pos += xvelocity*dt
dt+=1
current.axis = vec(0, 1, 0)
current.pos = vec(2, -3.5, 0)
dt = 1
yvelocity = vec(0, .1, 0)
while(dt<8):
rate(15)
current.pos += yvelocity*dt
dt+=1
negative1 = box(pos=vec(2, count, 0), size = vec(.25, .1, 0), color = color.blue)
dt = 1
current.axis = vec(-1, 0, 0)
current.pos = vec(2, 0, 0)
while(dt<8):
rate(15)
current.pos -= xvelocity*dt
dt+=1
positive1 = box(pos=vec(-2, count, 0), size = vec(.25, .1, 0), color = color.red)
positive1ish = box(pos=vec(-2, count, 0), size = vec(.1, .25, 0), color = color.red)
current.axis = vec(0,-1, 0)
current.pos = vec(-2, 0, 0)
dt = 1
while(dt<8):
rate(15)
current.pos -= yvelocity*dt
dt+=1
current.axis = vec(1, 0, 0)
current.pos = vec(-2, -3.5, 0)
dt = 1
while(dt<5):
rate(15)
current.pos += xvelocity*dt
dt+=1
count +=1
print("capacitor is charged, no more current is flowing")
Now, lets introduce our neutral metal bar (conductor). This code includes the conductor and the initial positions of the charges within
bar = box(pos=vec(0, 5, 0), size=vec(1, .8, 0), color = color.white) y1stRow1stCol = 5.15 y1stRow2ndCol = 5.3 y2ndRow1stCol = 5 y2ndRow2ndCol = 4.7 atomNeg1 = box(pos = vec(-.35,y1stRow1stCol,0), size = vec(.15, .05, 0), color =color.blue) atomPos1 = box(pos=vec(-.1, y1stRow1stCol, 0), size = vec(.15, .05, 0), color = color.red) atomPos1ish = box(pos=vec(-.1, y1stRow1stCol, 0), size = vec(.05, .15, 0), color = color.red) atomNeg2 = box(pos = vec(.1,y1stRow2ndCol,0), size = vec(.15, .05, 0), color =color.blue) atomPos2 = box(pos=vec(.35, y1stRow2ndCol, 0), size = vec(.15, .05, 0), color = color.red) atomPos2ish = box(pos=vec(.35, y1stRow2ndCol, 0), size = vec(.05, .15, 0), color = color.red) atomNeg3 = box(pos = vec(-.1,y2ndRow1stCol,0), size = vec(.15, .05, 0), color =color.blue) atomPos3 = box(pos=vec(-.35, y2ndRow1stCol, 0), size = vec(.15, .05, 0), color = color.red) atomPos3ish = box(pos=vec(-.35, y2ndRow1stCol, 0), size = vec(.05, .15, 0), color = color.red) atomNeg4 = box(pos = vec(.35,y2ndRow2ndCol,0), size = vec(.15, .05, 0), color =color.blue) atomPos4 = box(pos=vec(.1, y2ndRow2ndCol, 0), size = vec(.15, .05, 0), color = color.red) atomPos4ish = box(pos=vec(.1, y2ndRow2ndCol, 0), size = vec(.05, .15, 0), color = color.red)
Now, we add a loop that will move the bar magnet and charges downward (towards our capacitor) and polarize our magnet
barYpos = 5
atom1xPos = -.1
atom2xNeg = .1
atom3xNeg = -.1
atom4xNeg = .35
atom4xPos = .1
atom3xPos = -.35
while(atom1xPos < .35):
rate(15)
barYpos -= 5/9
y1stRow1stCol -= 5/9
y1stRow2ndCol -= 5/9
y2ndRow1stCol -= 5/9
y2ndRow2ndCol -= 5/9
atom1xPos = atom1xPos + .05
atom2xNeg = atom2xNeg - .05
atom3xNeg = atom3xNeg - (.25/9)
atom4xNeg = atom4xNeg - (.7/9)
atom4xPos = atom4xPos + (.25/9)
atom3xPos = atom3xPos + (.7/9)
bar.pos = vec(0, barYpos, 0)
atomNeg1.pos = vec(-.35, y1stRow1stCol, 0)
atomPos1.pos = vec(atom1xPos, y1stRow1stCol, 0)
atomPos1ish.pos = vec(atom1xPos, y1stRow1stCol, 0)
atomNeg2.pos = vec(atom2xNeg,y1stRow2ndCol,0)
atomPos2.pos = vec(.35, y1stRow2ndCol, 0)
atomPos2ish.pos = vec(.35, y1stRow2ndCol, 0)
atomNeg3.pos = vec(atom3xNeg, y2ndRow1stCol, 0)
atomPos3.pos = vec(atom3xPos, y2ndRow1stCol, 0)
atomPos3ish.pos = vec(atom3xPos, y2ndRow1stCol, 0)
atomNeg4.pos = vec(atom4xNeg, y2ndRow2ndCol, 0)
atomPos4.pos = vec(atom4xPos, y2ndRow2ndCol, 0)
atomPos4ish.pos = vec(atom4xPos, y2ndRow2ndCol, 0)
print("our conductor is now polerized")
Here is the GlowScript simulation: https://www.glowscript.org/#/user/abhairampally/folder/Public/program/MotionalEMFbyFaraday'sLaw. Be sure to play around with the code and rates of the loops to properly see the movement of charge as the bar magnet moves towards the capacitor!
Examples
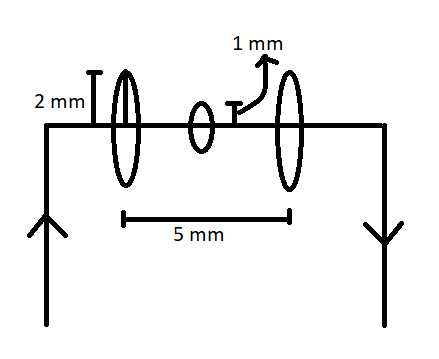
Using the figure below, identify the following.
- a) Direction of magnetic field
- b) Direction of change in magnetic field, [math]\displaystyle{ \frac{d\vec{B}}{dt} }[/math]
- c) Direction of negative change in magnetic field, [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math]
- d) Direction of current, [math]\displaystyle{ I }[/math]
- e) Polarization of moving bar
- f) Direction of electric field inside bar due to polarization
- g) Direction of force on bar
Click for Solution
SOLUTION:
- a) Into the page
- A circle with an 'x' inside of it represents a vector into the page. A circle with a dot inside represents a vector out of the page.
- b) Into the page
- Initially, at the time of the image, there are 4 circles representing magnetic field enclosed by the bars. However, as the bar moves, at some time t, the number of circles enclosed by the bar will increase; therefore, there is more magnetic field inside the loop. This means that the change in magnetic field is in the direction of the magnetic field.
- c) Out of the page
- The negative change in magnetic field is in the opposite direction as change in magnetic field.
- d) Counterclockwise
- Point your thumb in the direction of [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math]. Your fingers will curl in the direction of current.
- e) Positive charges at the top, negative charges at the bottom
- The magnetic force on a particle is [math]\displaystyle{ \vec{F} = q\vec{v} \times \vec{B} }[/math], so point your fingers in the direction of the velocity of the bar and curl them in the direction of magnetic field. The direction of your thumb is the direction of force on a positive particle.
- f) Down
- Positive charges have an electric field that points away from them while negative particles have an electric field that point towards them. If the top of the bar is positively charged, the field will point downward toward the negative particles.
- g) Left
- When a current is involved, [math]\displaystyle{ \vec{F} = I\vec{l} \times \vec{B} }[/math], so point your fingers in the direction of the length of the bar (in the direction of current) and curl them in the direction of magnetic field. The direction of your thumb is the direction of force on the bar.
Easy
A bar of length [math]\displaystyle{ L }[/math] slides to the right at constant speed [math]\displaystyle{ v }[/math] on two metal rails that are connected with a resistor [math]\displaystyle{ 2R }[/math]. There is a constant magnetic field [math]\displaystyle{ B }[/math] going out of the page. What is the magnitude of the [math]\displaystyle{ Emf }[/math] produced?
Click for Solution
SOLUTION:
- Because the magnetic field is constant throughout the area, the flux is equal to the magnetic field times the area. So we have that [math]\displaystyle{ \Phi_B = BA }[/math].
- Given that the bar has length [math]\displaystyle{ L }[/math], we call the changing width [math]\displaystyle{ w }[/math] and say that [math]\displaystyle{ A = Lw }[/math], so [math]\displaystyle{ \Phi_B = BLw }[/math].
- Next, we have from Faraday's Law that [math]\displaystyle{ |Emf| = | \frac{d\Phi}{dt}| }[/math]. So we need to take the derivative of the flux.
- This derivative is [math]\displaystyle{ \frac{d\Phi}{dt} = \frac{d}{dt} (BLw) }[/math].
- Since [math]\displaystyle{ B }[/math] and [math]\displaystyle{ L }[/math] are constant, these are unaffected by the derivative. So we can simplify the derivative to [math]\displaystyle{ \frac{d\Phi}{dt} = BL \frac{d}{dt} (w) = BLv }[/math]. Here, the derivative with respect to time of the width is given by [math]\displaystyle{ v }[/math], the velocity of the bar, since this is the change in the width.
- Therefore, the magnitude is given by [math]\displaystyle{ |Emf| = BLv }[/math].
Medium
A bar of length [math]\displaystyle{ L = 2 }[/math] is moving across two other bars in a region of magnetic field, [math]\displaystyle{ B = 0.0013T }[/math] directed into the page. The bar is moving with a velocity of 10 m/s, and [math]\displaystyle{ x }[/math] is the width of the area enclosed. What is the magnitude of the [math]\displaystyle{ emf }[/math] produced?
Click for Solution
SOLUTION:
- Because the amount of magnetic field enclosed by the system is changing with time, we must use Faraday's Law: [math]\displaystyle{ |emf| = \frac{d}{dt} \int\! \vec{B} \cdot \vec{n}dA }[/math]
- First, integrate through the formula: [math]\displaystyle{ |emf| = \frac{d}{dt} \left(\vec{B} \cdot A\right) }[/math]
- Change in area [math]\displaystyle{ \Delta{A} = L\Delta{x} }[/math]
- In this case, the distance [math]\displaystyle{ x }[/math] is changing and resulting in a change in area, so the formula becomes: [math]\displaystyle{ |emf| = \vec{B} \cdot L\frac{d}{dt}x }[/math]
- The derivative of distance is velocity. [math]\displaystyle{ \frac{dx}{dt} = v }[/math]
- Therefore, |emf| in this problem is equal to [math]\displaystyle{ BLv = .026 V }[/math]
Difficult
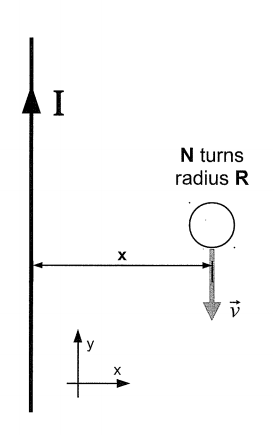
A long straight wire carrying current I = .3 A is moving with speed v = 5 m/s toward a small circular coil of radius R = .005 and 10 turns. The long wire is in the plane of the coil. The coil is very small, so that, at any fixed moment in time, you can neglect the spatial variation of the wire's magnetic field over the area of the coil.
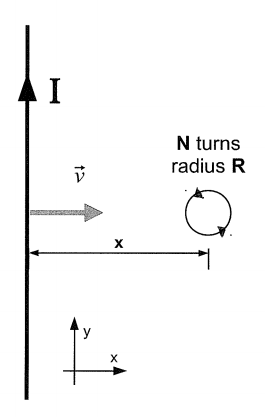
- a) Is the induced current in the coil flowing clockwise or counterclockwise?
- b) At the instant when the long wire is a distance x = 4 m from the center of the coil, determine the magnitude of the induced emf in the coil.
Now consider the case where the wire is stationary and the coil is moving down parallel to the wire with a constant speed, [math]\displaystyle{ v = 2 m/s }[/math].
- c) At the instant when the long wire is a distance x = 4 m from the center of the coil, determine the magnitude of the induced emf in the coil.
Click for Solution
SOLUTION:
- a) Counterclockwise
- Using the right hand rule, if you point your thumb in the direction of current (+y), your fingers will curl in the direction of magnetic field. In this case, magnetic field is pointing into the page at the coil. At the location of the coil, the magnitude of the magnetic field due to the wire is increasing as the wire moves closer; therefore, [math]\displaystyle{ \frac{d\vec{B}}{dt} }[/math] is pointing into the page, and [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math] is pointing out of the page. If you point your thumb in the direction of [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math], your fingers curl in the direction of the induced current.
- b) [math]\displaystyle{ |emf| = 1.47E-11 V }[/math]
- After integrating Faraday's Law, we get [math]\displaystyle{ |emf| = \frac{d}{dt} (\vec{B} \cdot A) }[/math]
- Notice that distance [math]\displaystyle{ x }[/math] is changing with time.
- After doing this derivative, we get [math]\displaystyle{ |emf| = \frac{\mu_0IR^2v}{2x^2} }[/math]
- This is the magnitude of emf for one loop in the coil, so we have to multiply it by the number of loops, [math]\displaystyle{ N }[/math].
- [math]\displaystyle{ |emf| = \frac{N\mu_0IR^2v}{2x^2} }[/math]
- c) |emf| = 0
- Remember that the emf relies on a changing magnetic field, which was dependent on a changing [math]\displaystyle{ x }[/math] in the previous example. Now, however, the coil is moving parallel to the wire, meaning there is no change in [math]\displaystyle{ x }[/math], and no change in magnetic field.
Connectedness
- As an AE major, I'm pleasantly surprised to know that motional EMF has a ton of applications in aerospace engineering. From electric propulsion to sensors to launch vehicles and even hypersonics, it shows up everywhere. Since I'm a huge fan of electric propulsion, I'm going to yap about that. In Hall thrusters, electrons are magnetised by a strong radial magnetic field and undergo an azimuthal E × B drift. Because the electrons are moving across a magnetic field, they experience a motional EMF (the v × B electric field), which plays a key role in cross-field electron transport. This is important because motional EMF influences the discharge current, electron mobility, ion acceleration, and ultimately the thrust efficiency of the thruster.
- Believe it or not, Faraday's law can be applied to musical instruments such as the electric guitar. In many electric instruments, 'pickup coils' sense the vibration of the strings, which causes variations in magnetic flux. These pickup coils often consist of magnet wrapped with a coil of copper wire, where the magnet creates a magnetic field and the vibrations of the string disturb the field, inducing a current in the coiled wire.
- I am a biomedical engineering student, and one application of Faraday's law in the medical field is transcranial magnetic stimulation. During this procedure, magnetic coils are used to stimulate small regions of the brain through electromagnetic induction. Current is discharged from a capacitor into the coil to produce pulsed magnetic fields. This technique can be used to evaluate and diagnose various conditions affecting the connection between the brain and muscles, including strokes and motor neuron diseases. It has also been said to alleviate the symptoms of major depressive disorder.
- I am currently majoring in mechanical engineering, and in this field, we are required to work with both mechanics and circuit-like scenarios. Personally, I am interested in going into the car manufacturing industry, where motional emf plays a very important role. When you move an object through a magnetic field, it resists movement and generates electricity in the loop. If this is done with enough force, it could be used to stop a small car or roller-coaster.
- I am a biomedical engineering major and I have found a surprising amount of connections between Faraday’s law and my major. One such connection is how MRI machines utilize Faraday's law to generate images of tissues/organs. A magnetic field is applied to align atomic spins within the body, and then varying magnetic fields (generated by coils) are applied to said hydrogen atoms, inducing EMF signals from the newly aligned atoms. These EMF signals are collected and later used to provide an image of the tissue or organ in question.
History
Before 1831, the only known way to produce a steady electric current was through a chemical source such as a battery. Physicists believed the current required direct contact between the conductors and nothing suggested that motion or magnetic fields could generate electricity. This changed when Michael Faraday began a series of experiments on electromagnetic induction. He discovered that a current could be produced in a closed loop without a battery, either by moving a conductor through a magnetic field or by changing the magnetic field threading the loop.
Faraday did not initially distinguish between what we now call motional EMF and transformer EMF. Instead, he described them using his concept of lines of magnetic force being cut by the conductor. As he was an experimentalist and didn't have much math background, he came up with the idea which later became [math]\displaystyle{ \mathcal{E} = -\frac{d\Phi_B}{dt} }[/math]. The negative sign was introduced in 1834 by Heinrich Lenz, who said that the induced EMF always acts to oppose the change causing it (Lenz's law).
It was James Maxwell who later gave Faraday's discoveries their mathematical form. Maxwell incorporated induction into what would famously become the Maxwell-Faraday equation, showing that a changing magnetic flux inevitably produces an electric field with a non-zero curl.
See also
You may want to explore the process of calculating motional emf before the use of Faraday's Law. Maxwell's equations and circuits with resistance are also relevant and may be worth looking into.
Motional emf problems can be pretty tricky depending on what the question is asking you to do. It's always a good idea to know how each formula came about, and how it can change bases on different scenarios. This includes the formula for resistance in a circuit, [math]\displaystyle{ V = IR }[/math]. A problem could go as far as to give you a resistance for a circuit, ask you to solve for the potential difference, [math]\displaystyle{ V }[/math], or [math]\displaystyle{ emf }[/math], and then ask you to solve for the current as well.
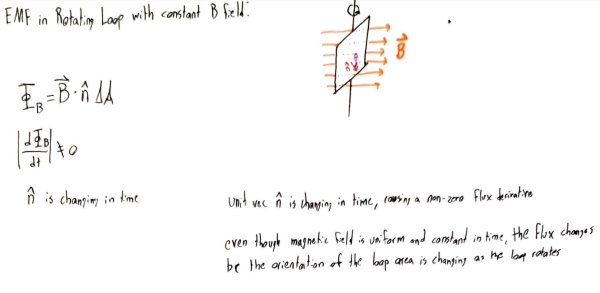
One of the most difficult versions of a Motional EMF problem that probably won't be covered on an exam, but could be interesting, is that of a rotating loop.
This illustration gives a pretty good idea of how the problem is different, but actually very similar to previous ones as the equation now accounts for change in N as opposed to change in A. To get some practice with this new application, try replacing the changing area with a changing orientation in a previous problem, and remember that your period for taking the integral will be from 0 to pi (or whatever starting point is specified). For the most part, this application is out of the scope of Physics Two, so the most helpful resources you will be able to find will be from videos related to the topic on Youtube, Khan Academy,...
Lastly, I advise you to become familiar with Lenz's law because it gives the direction of the induced emf and current resulting from electromagnetic induction.
Further reading
- SparkNotes: SAT Physics
- Matter & Interactions, Vol. II: Electric and Magnetic Interactions, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)
External links
- Video Explanation: https://www.youtube.com/watch?v=Wgtw5lPKFXI
- Text Explanation: https://openstax.org/books/university-physics-volume-2/pages/13-3-motional-emf
References
https://en.wikipedia.org/wiki/Faraday%27s_law_of_induction
http://farside.ph.utexas.edu/teaching/em/lectures/node43.html
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html#c4
https://en.wikipedia.org/wiki/Pickup_(music_technology)
http://www.physics.princeton.edu/~mcdonald/examples/guitar.pdf
https://en.wikipedia.org/wiki/Transcranial_magnetic_stimulation#Technical_information
https://www.physicsbootcamp.org/Motional-EMF.html
https://en.wikipedia.org/wiki/Faraday's_law_of_induction#Motional_emf