Motional Emf
Claimed by Krupa Patel (Fall 2025)
Motional emf is an electromagnetic field caused by current that is produced through the motion of a conductor in a magnetic field. Polarization of the bar occurs which is similar to the Hall effect except that the Hall effect involves polarization through the force of a magnetic field on charged particles that are already moving inside a motionless conductor. Motional emf is difficult to observe visually using batteries, light bulbs, and compasses because it is so small.
Note: This page does involve the use of Faraday's Law.
The Main Idea
Moving a metal bar (or similar conductive material) will naturally also move the mobile charges within the metal bar. if this is done in a magnetic field it will create a magnetic force, which acts on the charged particles inside the bar polarizing it (charge separation). This makes the bar similar to a battery which means that If the bar is part of a circuit, the magnetic force produced causes a current to run through it.
Edited by Aya Petrenko (Fall 2023)==
EMF occurs when the movement of a bar along rails connected to a resistor (effectively creating a circuit) induces an increase in magnetic flux through said circuit. In a short time (dt), the bar moves a distance of [math]\displaystyle{ dx = v \times dt }[/math], and the area surrounded by current-carrying circuit pieces increases by the quantity [math]\displaystyle{ dA = L \times dx = L \times v \times dt }[/math] (where L = length of bar). Again, the result is increased magnetic flux through the circuit.
[math]\displaystyle{ \Delta \Phi }[/math] (Magnetic flux) = (B-field) * (dA - change in area) = B(L*v*dt)
Dividing by dt, we get:
[math]\displaystyle{ \frac{dI_B}{dt} = \frac{B \times L \times v \times dt}{dt} = B \times L \times v }[/math]. This is the case assuming bar velocity is perpendicular to the magnetic field inside the circuit.
Emf is equal to the magnitude of the change in magnetic flux over time. Therefore,
emf = [math]\displaystyle{ \left| \frac{dI_B}{dt} \right| }[/math] = rate of change of magnetic flux
With motional emf, usually several cases cases will occur: the area surrounded by the circuit changes while the magnetic field is uniform and constant, or both the area and magnetic field are changing in magnitude. If the second scenario occurs, we can use the product rule to find the value of the rate of change in magnetic flux:
[math]\displaystyle{ \frac{dI_b}{dt} = \frac{d}{dt}(B \cdot A) }[/math]
[math]\displaystyle{ \frac{dI_b}{dt} = \left( \frac{dB}{dt} \cdot A \right) + \left( B \cdot \frac{dA}{dt} \right) }[/math]
[math]\displaystyle{ \frac{dI_b}{dt} = \left( \frac{dB}{dt} \cdot A \right) + \left( B \cdot L \cdot \frac{dx}{dt} \right) }[/math]
[math]\displaystyle{ \frac{dI_b}{dt} = \left( \frac{dB}{dt} \cdot A \right) + \left( B \cdot L \cdot v \right) }[/math]
To get a further glimpse into how the basic emf expression (BLv) is derived, we must recall the concept of potential difference:
Electrical Potential difference (dV) = E (Electric Field) * d (distance between two points)
Because we are trying to find the potential difference across a conducting bar, "d" can be replaced with "L", the length of the bar.
dV = E * L (length of bar)
The value of the electric field is derived from the Lorentz force equation, listed below:
[math]\displaystyle{ F = q(E_{\text{perp}} + v \times B) }[/math] [math]\displaystyle{ |E_{\text{perp}}| = |v_{\text{bar}}||B| }[/math]
Therefore, [math]\displaystyle{ dV_{\text{bar}} = E_{\text{perp}} \times L = |\bar{v}||B||L| }[/math]
Additionally, when the metal bar is polarized, because of the charge separation, an electric force is created in the bar opposite to the magnetic force on charged particles.
Polarization and Steady State
Polarization occurs due to the shift of the mobile electron sea in one direction caused by the magnetic force. Eventually, the shifting will stop when enough electrons will shift in a particular direction so that the electric force, in the opposite direction, balances out the magnetic force ([math]\displaystyle{ qvB=qE }[/math]). Consequently, in the steady state, [math]\displaystyle{ E=vB }[/math] and there is no net force on the bar, so the bar does not require any additional force to keep it moving at a constant velocity, assuming it moves in a frictionless environment.
In the steady state, a nonzero E-field exists inside the metal bar; however, if the bar is not connected in a circuit, there is no current. This is because the electric force is balanced with the magnetic force, resulting in zero net force on the mobile electrons. The potential difference across the metal bar is then the product of the electric field and the length of the bar.
Driving Current
If the metal bar is used to form a circuit, where the bar is slid along on two frictionless metal rails that are also connected, then the bar's polarization in the bar mimics a battery and can drive a current through the bar and the rails it slides on, given the bars are connected at some other point.
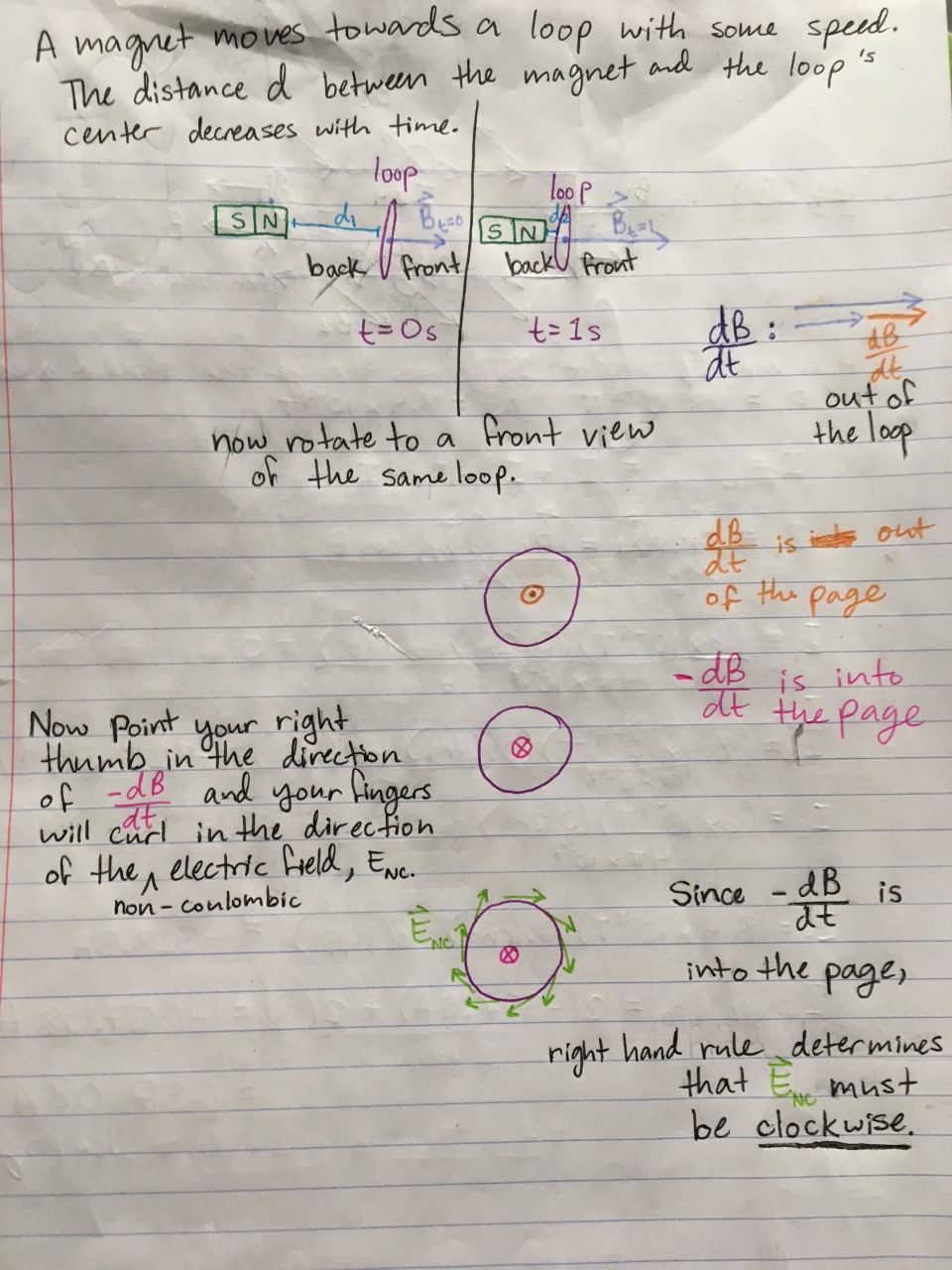
Once the bar, moving within the magnetic field, has a velocity, the direction of the magnetic force can be determined through the right-hand rule. There will be a magnetic force in the direction of the length of the bar on the electrons which will cause the electrons to have a small velocity through the bar. This is in addition to the velocity caused by the moving bar. In the diagram shown on the left the velocity vector of the electrons would be [math]\displaystyle{ \lt V_{bar}, V, 0 \gt }[/math]. Magnetic force on the electrons is [math]\displaystyle{ \lt -e*V*B,-e*V_{bar}*B, 0\gt }[/math]. B is the magnetic field being applied. It is clear that there is a magnetic force on the electrons that is opposite to the horizontal force of the moving bar. This means that the horizontal net force for the bar is [math]\displaystyle{ F_{net} = F_{applied} - N*V*B*e }[/math] with N being the number of mobile electrons. If the bar moves at higher speeds, the vertical magnetic force on the electrons becomes greater along with the vertical velocity of the electrons. This in turn, increases the magnetic force to the left of the bar. If the bar continues to accelerate, the horizontal net force will get smaller and smaller until it reaches zero at which point the bar will move at a constant velocity with one force pulling it in one direction and the magnetic force pulling it in the opposite direction. A current now runs through the bar. The mobile electrons in the bar move toward the negatively charged end, rather than the positively charged end, because the continuous depletion of charge means that the electric field is always slightly less than what is needed to balance out the opposing magnetic field. Therefore, the electrons move to the negative end to maintain charge separation and the electric field.
The potential difference across the bar is still the product of the electric field and the length of the bar. If the bar does have some resistance, then it is treated like a battery with internal resistance. In the circuit, the potential difference round-trip for the entire circuit is zero.
Ideal Conditions
Motional emf is difficult to observe with light bulbs and batteries because it is relatively small. In order to obtain a sizeable emf, a large magnetic field (B) needs to be applied over large regions (L) all the while the bar is moving at great velocities (V) through the region. If dealing with a wire, adding multiple turns will also help. Even then if you have a large emf, it only lasts for a little amount of time. Also detectors like lightbulbs and compasses are not very sensitive, so in order to actually detect motional emf more sensitive equipment is needed.
A Mathematical Model
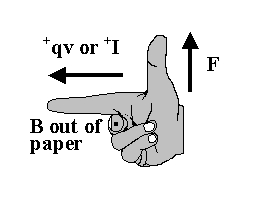
The potential difference across the metal bar is [math]\displaystyle{ \Delta V=emf=EL=v_{bar}BL }[/math]. If the bar has resistance, then [math]\displaystyle{ \Delta V=emf-r_{int}I }[/math].
When the bar in the circuit, in steady state, moves a distance [math]\displaystyle{ \Delta x }[/math] over a time [math]\displaystyle{ \Delta t }[/math], the work done is [math]\displaystyle{ F \Delta x }[/math] and the power supplied is [math]\displaystyle{ {F \Delta x}/{\Delta t} }[/math], or [math]\displaystyle{ Fv_{bar} }[/math]. If the rails in the circuit are connected by a resistor, then the power dissipated in the resistor is [math]\displaystyle{ ILBv_{bar}=I*emf={emf/R}*emf={emf^{2}}/R=RI^{2} }[/math].
Motional emf can be calculated in terms of magnetic flux: [math]\displaystyle{ \left | emf \right |=\left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right | }[/math].
Equations to remember
1. [math]\displaystyle{ \left | emf \right |=\left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right | }[/math].
2. During steady state, the electric force balances with the magnetic force([math]\displaystyle{ qvB=qE }[/math]), so [math]\displaystyle{ E=vB }[/math].
3.We know [math]\displaystyle{ \Delta V=emf }[/math],
[math]\displaystyle{ \Delta V=EL }[/math],
and [math]\displaystyle{ E=vB }[/math],
so [math]\displaystyle{ \Delta V=v_{bar}BL }[/math].
4. Power [math]\displaystyle{ P=I\Delta V }[/math] so [math]\displaystyle{ P=I(IR)=I^{2}R }[/math].
5.[math]\displaystyle{ emf = {\frac{q(\vec{v} \times \vec{B})L}{q}} = v*B*L }[/math] where v is the velocity of the bar and L is the bar length
A Computational Model
A simulation of motional emf can be found here.
Another visual, GlowScript model can be found at the following: [1].
Examples
Simple
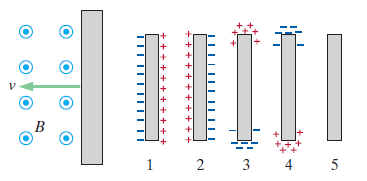
Taken from the Matter & Interactions textbook, variation of P60.
A neutral iron bar is dragged to the left at speed v through a region with a magnetic field B that points out of the page, as shown above. (a) In which direction is the magnetic force? (b) Which diagram (1–5) best shows the state of the bar?
(a) The magnetic force points upwards. Use the right hand rule.
(b) Diagram 3 shows the correct polarization based on the direction of the magnetic force.
Middling
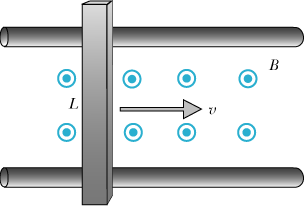
Taken from the Matter & Interactions textbook, variation of P63.
A neutral metal rod of length 0.21 m slides horizontally at a constant speed of 7 m/s on frictionless insulating rails through a region of uniform magnetic field of magnitude 0.18 tesla, directed out of the page as shown in the diagram. (a) Is the top of the moving rod positive or negative? (b) After the initial transient, what is the magnitude of the net force on a mobile electron inside the rod? (c) What is the magnitude of the electric force on a mobile electron inside the rod? (d) What is the magnitude of the magnetic force on a mobile electron inside the rod? (e) What is the magnitude of the potential difference across the rod? (f) In what direction must you exert a force to keep the rod moving at constant speed?
(a) The top of the moving rod is negative. Use the right-hand rule.
(b) [math]\displaystyle{ \left | \overrightarrow{F}_{net} \right |=0 \: N }[/math] because after the initial transient the system is in steady state and the electric force balances out the magnetic force.
(c) First we recognize that the system is in steady state, so [math]\displaystyle{ E=vB=7 \times 0.18=1.26 }[/math]. Then [math]\displaystyle{ \left | \overrightarrow{F}_{E} \right |=\left | qE \right |=\left | -1.6 \times 10^{-19}(1.26) \right |=2.016 \times 10^{-19} \: N }[/math].
(d) In steady state, [math]\displaystyle{ \left | \overrightarrow{F}_{E} \right |=\left | \overrightarrow{F}_{B} \right | }[/math]. So, [math]\displaystyle{ \left | \overrightarrow{F}_{B} \right |=2.016 \times 10^{-19} \: N }[/math].
(e) [math]\displaystyle{ \Delta V=EL=v_{bar}BL=7 \times 0.18 \times 0.21=0.2646 \: V }[/math].
(f) No force is needed. The system is in steady state, so no additional force needs to be applied to keep the rod at constant speed.
Difficult
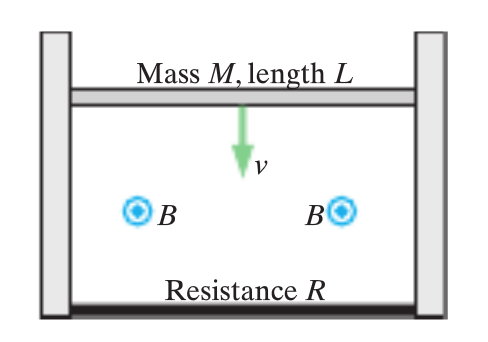
Taken from the Matter & Interactions textbook, P64.
A metal bar of mass M and length L slides with negligible friction but with good electrical contact down between two vertical metal posts, as shown above. The bar falls at a constant speed v. The falling bar and the vertical metal posts have negligible electrical resistance, but the bottom rod is a resistor with resistance R. Throughout the entire region there is a uniform magnetic field of magnitude B coming straight out of the page. (a) Calculate the amount of current I running through the resistor. (b) What is the direction of the conventional current I? (c) Calculate the constant speed v of the falling bar. (d) What is the direction of the electric force acting on a positive mobile charge? (e) What is the direction of the magnetic force acting on the bar?
(a) The bar is already falling at a constant velocity, so [math]\displaystyle{ \left | \overrightarrow {F}_{net} \right |=0 }[/math] and [math]\displaystyle{ E=vB }[/math]. We know that [math]\displaystyle{ I={emf}/R }[/math] and [math]\displaystyle{ {emf}=EL=vBL }[/math] so it follows that [math]\displaystyle{ I={vBL}/R }[/math].
(b) The magnetic force [math]\displaystyle{ qvB }[/math] causes positive charges to move left and negative charges to move right. Conventional current flows from the positively charged end of the bar to the negative end, so it runs counterclockwise.
(c) The conventional current I running through the bar causes a magnetic force upwards of magnitude [math]\displaystyle{ ILB\sin 90^{\circ}=({vBL}/R)LB={vL^{2}B^{2}}/R }[/math]. This magnitude must balance out the gravitational force [math]\displaystyle{ Mg }[/math] because the magnetic and gravitational forces must cancel for [math]\displaystyle{ \left | \overrightarrow {F}_{net} \right |=0 }[/math] and the bar to have a constant velocity v. So, setting the forces equal to each other, [math]\displaystyle{ v={MgR}/{L^{2}B^{2}} }[/math].
Note: We can also find the speed of the falling bar with [math]\displaystyle{ \left | emf \right |=\left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right | }[/math]. Using the loop rule, [math]\displaystyle{ 0=IR - {emf} }[/math]. So [math]\displaystyle{ \left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right |=IR }[/math]. We can transform that to [math]\displaystyle{ IR=\frac{\mathrm{d} (BA)}{\mathrm{d} t} }[/math]. Since B is constant, [math]\displaystyle{ IR=B(\frac{\mathrm{d} (A)}{\mathrm{d} t}) }[/math]. We can transform that to [math]\displaystyle{ IR=B(\frac{\mathrm{d} (Lh)}{\mathrm{d} t}) }[/math], where h is the distance of the bar above the bottom rod. Since L is constant, [math]\displaystyle{ IR=BL(\frac{\mathrm{d} (h)}{\mathrm{d} t}) }[/math]. [math]\displaystyle{ \frac{\mathrm{d} (h)}{\mathrm{d} t}) }[/math] is the velocity of the bar, so [math]\displaystyle{ IR=BLv }[/math]. Solving for v, [math]\displaystyle{ v={MgR}/{L^{2}B^{2}} }[/math].
(d) The electric force acting on a positive mobile charge points towards the right in the bar. Using the right hand rule, with B pointing out of the page, v pointing downwards, we know that the magnetic force points to the right. This means that the bar is polarized with positive charges on the left side of the bar and negative charges on the right side. The electric force points from positive charges to negative charges, so the electric force points towards the right.
(e) The magnetic force acting on the bar points upwards. We know that current flows from left to right in the bar because positive charges are polarized on the left side of the bar and negative charges are on the right side of the bar. Using the right hand rule, with B pointing out of the page and current pointing to the right, we find that the magnetic force points upwards.
https://drive.google.com/file/d/15HiDCO1dNy676X7_sm1yWiYb87Dn_fY3/view?usp=drivesdk
https://drive.google.com/file/d/14Q_EItpjeq9cmCD3Gj8aMOUsARM3UyOE/view?usp=drivesdk
Connectedness
The concept of power generated from a mechanical input is how electric generators function. The mechanical energy is commonly supplied by falling water at dams or expanding steam in turbines.
Motional emf is also applied in the DC motors of airplanes, when mechanical energy is transformed into electrical energy. Additionally, motional emf is applied in breaking systems. When an object moves through a magnetic field, it resists the change(movement) by converting the mechanical energy into electrical energy. So if an object moves with a sufficient amount of force to move, through a magnetic field, it can convert enough mechanical energy to stop a system. This concept is applied in, for example, roller coasters.
History


The phenomenon of electromagnetic induction, the emf produced from the interactions between a magnetic field and an electric circuit, was discovered independently in 1831 by Michael Faraday and 1832 by Joseph Henry (Faraday published his results first). Many of Faraday's ideas were rejected by the scientists of the day because they had no mathematical basis, but James Clerk Maxwell used these ideas to formulate his electromagnetic theory and the Maxwell equations.
At the time, it was not well understood how Maxwell's equations related to moving charged objects. J.J. Thomson was the first to attempt to derive, from Maxwell's equations, an equation describing effects on moving charged particles, and Oliver Heaviside built upon this work and fixed errors in Thomson's derivation. In 1892, Hendrik Lorentz finally derived the correct equation called the Lorentz force. The magnetic force component of the Lorentz force describes motional emf, as the magnetic force pushing electrons in the moving charged object induces the emf.
See also
- Motional Emf using Faraday's Law: An expansion of this concept
- Lorentz Force: Combining electric and magnetic forces
- Generator: Real-world application
- Right-Hand Rule: How it works and other RHRs
Further reading
- Matter & Interactions, Vol 2
- The Feynman Lectures on Physics, Vol 2, Ch 16
External links
References
- Matter & Interactions Vol 2
- MIT OpenCourseWare
- A Brief History of The Development of Classical Electrodynamics