Lorentz Force
Claimed by Srihitha Jagarlamudi, Fall 2025
Introduction
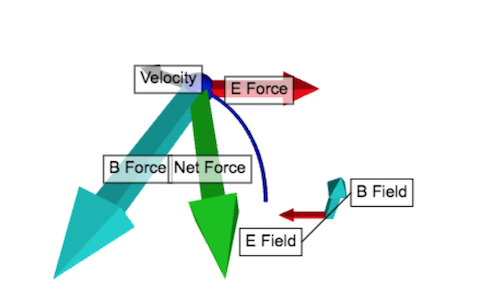
The **Lorentz force** is a fundamental concept in electromagnetism, describing the force experienced by a charged particle moving through electric and magnetic fields. It is important in understanding the behavior of particles in various physical systems.
Formally, the Lorentz force is expressed as:
[math]\displaystyle{ \vec{F} = q\vec{E} + q\vec{v} \times \vec{B} }[/math]
where:
- [math]\displaystyle{ q }[/math] is the electric charge of the particle,
- [math]\displaystyle{ \vec{E} }[/math] is the electric field,
- [math]\displaystyle{ \vec{v} }[/math] is the velocity of the particle,
- [math]\displaystyle{ \vec{B} }[/math] is the magnetic field.
This equation shows how electric fields exert forces in the direction of the field, while magnetic fields exert forces perpendicular to both the particle’s motion and the magnetic field lines. The relationship explains why electric fields can either slow down or sped up particles. The Lorentz force not only underpins the operation of electric motors, generators, and particle accelerators, but also provides a framework for deeper exploration of classical and modern physics.
The Main Idea
The **Lorentz force** is the total electromagnetic force experienced by a charged particle due to electric and magnetic fields. When a particle with charge [math]\displaystyle{ q }[/math] moves with velocity [math]\displaystyle{ \vec{v} }[/math] in the presence of an electric field [math]\displaystyle{ \vec{E} }[/math] and magnetic field [math]\displaystyle{ \vec{B} }[/math], the net force acting on the particle is given by:
[math]\displaystyle{ \vec{F}_{\text{Lorentz}} = q\vec{E} + q\vec{v} \times \vec{B} }[/math]
This equation shows two distinct contributions:
- The electric force: [math]\displaystyle{ q\vec{E} }[/math], which acts in the direction (or opposite direction, depending on the sign of the charge) of the electric field.
- The magnetic force: [math]\displaystyle{ q\vec{v} \times \vec{B} }[/math], which acts perpendicular to both the velocity of the particle and the magnetic field.
The direction of the magnetic force is determined using the **right-hand rule** for positive charges, and reverses for negative charges. The **magnitude** of the magnetic component of the force is given by:
[math]\displaystyle{ F_{\text{mag}} = qvB\sin\theta }[/math]
where [math]\displaystyle{ \theta }[/math] is the angle between [math]\displaystyle{ \vec{v} }[/math] and [math]\displaystyle{ \vec{B} }[/math].
In classical physics, the Lorentz force is the foundation of many electromagnetic phenomena, including the motion of charges in fields, current generation in wires, and the operation of electric and magnetic devices.
examples:
Significance
The Lorentz force complements Maxwell's equations by describing the force on a charged particle in electromagnetic fields. While Maxwell's equations define how fields are generated, the Lorentz force explains how particles respond to those fields.
This law is central to understanding:
Particle motion in fields: Determining the trajectories of electrons, ions, etc.
Magnetic field generation from currents, and explaining why currents exert forces on each other.
Applications such as electromagnets and transformers: Many devices rely on the Lorentz force, such as mass spectrometers, Hall Effect sensors, etc.
However, it does not fully describe collective particle behavior in materials, which requires more complex models like transport equations. Though the Lorentz force has quite a range of usefulness, the law describes only the behavior of individual particles. When looking at more complex figures or larger groups of charged particles, other forces will also need to be considered.
Overall, the Lorentz force has connections between electromagnetic theory and the motion of matter, which makes it a very significant law in physics.
A Mathematical Model
The electromagnetic force F on a charged particle, the Lorentz force (named after the Dutch physicist Hendrik A. Lorentz) is given by:
[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math]
where [math]\displaystyle{ q\vec{E} }[/math] is the electric force contributed by an external electric field and [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] is the magnetic force contributed by an external magnetic field. As many applications involve vectors, it is valuable to recognize the resulting directions of [math]\displaystyle{ q\vec{E} }[/math] and [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] in relation to the particle's charge and velocity within the environment of applied electric/magnetic fields. The resulting electric force vector will always be towards or opposite to the applied electric field, depending on the sign of the charge. For example, if an electron is in an electric field along the +x direction, the force will point in the -x direction. The magnetic force is always perpendicular to both the direction of motion and the field. The magnetic force on the particle, however, has a direction perpendicular to both the velocity v of the particle and the magnetic field B, and has a value proportional to q and to the magnitude of the vector cross product [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math]. More specifically, the magnitude of the magnetic force equals qvBsinθ where θ is the angle between v and B.
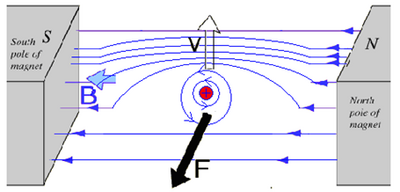
Motion of a Charged Particle in a Uniform Magnetic Field
A noteworthy result of the Lorentz force is the motion of a charged particle within a uniform magnetic field as the angle between v and B varies. If a scenario presents a charged particle with a velocity vector v perpendicular to the applied magnetic field B (i.e. θ = 90°), the particle will follow a circular trajectory. The radius of this trajectory can easily be calculated:
[math]\displaystyle{ \vec{F}_{Mag} = \vec{F}_{Centripetal} }[/math]
[math]\displaystyle{ qvB = mv^2/R }[/math]
[math]\displaystyle{ R = mv/qB }[/math]
Suppose that for the following example, a charge is shot into a region filled with a uniform magnetic field coming out of the page:
At every instant, the external magnetic field B points out of the page and thus invokes a magnetic force on the particle perpendicular to the particle's velocity - the force needed to create circular motion. The radius R can be calculated from the equation above. In addition, it's worth noting that the particle's charge will determine where the particle veers. If the particle were positively charged, the magnetic force would cause the particle to veer downward (due to right hand rule), and vice-versa if negatively charged.
In the case that θ is less than 90°, the particle's trajectory will orbit a helix path with a central axis parallel to the field lines.
If θ is zero, that is, the magnetic field is in the same direction as the particle's velocity, the particle will experience no magnetic force and continue to move normally along the field lines.
A Computational Model
Here is a visualization on VPython of a negatively charged particle moving through a constant electric and magnetic field:
Initially, a negatively charged particle is traveling with initial velocity in the -z direction. There is a constant electric field E in the -x direction and a constant magnetic field B in the +y direction. The magnetic force on the negatively charged particle is equal to [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math], or the charge of the particle times the cross product of the particle’s velocity and the magnetic field it travels through. The electric force on the particle is equal to [math]\displaystyle{ q\vec{E} }[/math], or the charge of the particle times the electric field that the particle travels through. Since the magnetic force on the particle is related to the particle’s velocity v, the magnetic force changes as the the particle’s velocity changes. Conversely, the electric force on the particle is constant. Since the Magnetic force is variable, the Lorentz Force on the particle, or the net force due to magnetic and electric forces on the particle ([math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math]) is also variable, and the particle's velocity changes.Over time, the interaction between the electric and magnetic forces will produce a sideways drift of the charged particles.
Example Problems
Simple
A charged particle experiences an electric force of <50, -120, 80> N and a magnetic force of <-30, 60, -40) N. Find the Lorentz Force.
Solution: <50, -120, 80> + <-30, 60, -40> = <20, -60, 40> N
The electric force on a certain particle is <100,-600,300> N and the magnetic force is <-600,400,0> N. Find the Lorentz force.
Solution: Lorentz force = <-500,-200,300> N

Intermediate
The magnetic force on a proton is 100 N at an angle 30 degrees down from the +x axis. The electric force on the proton is 100 N at an angle 30 degrees up from the +z axis. What is the magnitude of the Lorentz Force on the proton?
Solution: Lorentz force = 122.5 N
Difficult
An electron is traveling with a constant velocity of <0.75c, 0, 0>. You measure the magnetic field to be <0.4, 0.3, 0.5>T everywhere. What is the electric field?
Solution: E = <0, 1.13e8, -6.75e7> N/C
Since the electron is traveling at constant velocity, the net force must be zero. Thus, the magnetic field must equal the electric field, or [math]\displaystyle{ q\vec{v} ⨯ \vec{B}= q\vec{E} }[/math]. The charge on both sides cancels out to give [math]\displaystyle{ \vec{v} ⨯ \vec{B}= \vec{E} }[/math]. Calculating [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] = <0, -1.13e8, 6.75e7>, so the electric field must point in the opposite direction.
Connectedness
1. Speakers use the Lorentz force of an electromagnet to move a cone that creates sound waves in the air. When current flows through the wires in the electromagnetic in different quantities, the speakers move in unique ways to produce the different sounds that we recognize. Amplifiers for electric guitars and basses work in the same way.
2. In today's evolving world, one area of particular interest is sustainable and renewable energy. Wind turbines and hydropower plants work by harnessing the kinetic energy of wind or water and using it to induce an electrical current. The turbines rotate and move a permanent magnet that induces a current in an electromagnet placed inside of the magnet, which is shaped like a hollow cylinder. The induced current is then carried via wires to external sources to provide energy.
3. Several industries manufacture products that induce current using the Lorentz Force. For example, electric guitars and basses work by magnetizing the strings and relying on the Lorentz force to create a current in pickups that is then transmitted to an amplifier. Pickups are small electromagnet coils surrounding a magnet that are placed beneath the strings. The strings become magnetized because of the magnet inside the pickup. When they are played and vibrate, they induce current in the electromagnet. The Lorentz force causes the strings to exert forces that move mobile charges and induce the current. The current is then increased through a potentiometer and sent to an amplifier through a cable. In addition, charged particle accelerators like cyclotrons make use of the circular orbit particles experience when v and B are perpendicular to each other. For each revolution, a carefully timed electric field offers additional kinetic energy to cause the particles to move in increasingly-larger orbits until the desired energy level is met. These particles are known to be extracted and used in a number of ways, from basic studies of the properties of matter to the medical treatment of cancer.
Applications
Cyclotrons and particle accelerators exploit the Lorentz force to guide and accelerate particles. When \vec{v} is perpendicular to \vec{B}, particles orbit in circles and gain energy through electric fields.
Used in:
Particle physics (e.g., CERN experiments)
Radiation therapy
Mass spectrometry
More: Specific applications of the Lorentz force have enabled some of the most significant scientific experimentation to date.
It is known that when the angle between v and B is 90 degrees, there is no magnetic force on the particle which continues to move unaffected along the field lines. Cyclotrons and other charged particle accelerators make use of this fact and that particles move in circular orbit when v and B are perpendicular with respect to each other (therefore their cross product is equal to 0). With each revolution, these particles gain additional kinetic energy from the electric field which therefore increases orbit. Once reaching the desired energy level, they can be extracted and used in various ways from studies on subatomic particles to even medical treatments for diseases like cancer.
Scientists at the European Organization for Nuclear Research(CERN), the largest organization for particle research, take advantage of the Lorentz force in their collider experiments[4].
Furthermore, Mass spectrometers rely on the Lorentz force in order to separate charged particles based on the ratio of mass and charge. When ions are generated, the electric field accelerates them to gain kinetic energy. When the ions enter a perpendicular magnetic field, the Lorentz force magnetic component will cause them to follow a more curved trajectory.
Mass spectrometry is an application that is quite important in various fields such as chemistry and environmental science, as well as for identifying compounds that may be unknown, analyzing structures, etc. Without the Lorentz force, the accuracy would not be possible, making it vital in numerous scientific fields.
History
[[

The Lorentz Force is named after Hendrik Lorentz, who derived the formula in the late 19th century following a previous derivation by Oliver Heaviside in 1889. However, scientists had tried to find formulas for one electromagnetic force for over a hundred years before.Some scientists such as Henry Cavendish argued that the magnetic poles of an object could create an electric force on a particle that obeys an inverse-square law. However, the experimental proof was not enough to definitively publish. In 1784, Charles de Coulomb, using a torsion balance, was able to definitively show through experiment that this was true. After Hans Christian Ørsted discovered that a magnetic needle is acted on by a voltaic current, Andre Marie Ampere derived a new formula for the angular dependence of the force between two current elements. However, the force was still given in terms of the properties of the objects involved and the distances between, not in terms of electric and magnetic fields or forces.
Michael Faraday introduced modern ideas of magnetic and electric fields, including their interactions and relations with each other, later to be given full mathematical description by William Thomson (Lord Kelvin) and James Maxwell. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, it was not initially evident how his equations related to the forces on moving charged objects. J.J. Thomson was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as [math]\displaystyle{ \vec{F} = q\vec{E} + \frac{q}{2}\vec{v} ⨯ \vec{B} }[/math]. Finally, Heaviside and later Lorentz were able to combine the information into the currently accepted Lorentz Force equation.
See also
The Hall Effect is a special case in which the magnetic and electric forces on a particle or object cancel out, meaning that there is zero net force. Solving these problems involves setting the two forces equal to each other and using given information to find values for [math]\displaystyle{ \vec{B} }[/math], [math]\displaystyle{ \vec{v} }[/math], or [math]\displaystyle{ \vec{E} }[/math].
This video demonstrates a few everyday applications and examples of the Lorentz Force.
Further reading
- http://hyperphysics.phy-astr.gsu.edu/HBASE/hframe.html
- http://www.ittc.ku.edu/~jstiles/220/handouts/section%203_6%20The%20Lorentz%20Force%20Law%20package.pdf
External links
[1]*http://jnaudin.free.fr/lifters/lorentz/ [2]*https://nationalmaglab.org/education/magnet-academy/watchplay/interactive/lorentz-force [3]*http://web.mit.edu/sahughes/www/8.022/lec10.pdf [4]*https://www.lhc-closer.es/taking_a_closer_look_at_lhc/0.lorentz_force
References
- Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2.
- Jackson, John David (1999). Classical electrodynamics (3rd ed.). New York, [NY.]: Wiley. ISBN 0-471-30932-X.
- Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X.
- Hughs, Scott. “Magnetic Force; Magnetic Fields; Ampere's Law.” MIT.edu. Magnetic Force; Magnetic Fields; Ampere's Law, 29 Nov. 2017, Boston, MIT, Magnetic Force; Magnetic Fields; Ampere's Law.