Molecules
Claimed by Corinne Hill Fall 2022
Molecules
Atoms are essential in the creation of large-scale objects, but along the process of creating something fully realized, molecules are the essential link. Were it not for the chemical bonding between atoms, molecules would not exist, and therefore the infinite amount of forms matter can take on (i.e. a human, an apple, or a mountain) would be impossible. The universe would be a bowl filled with single-atom soup. Molecules allow for diversification in matter and allow the world we live in today to be so unique. While it may be apparent to see the need for molecules, oftentimes the "how" they are created is oversimplified and explained as chemical bonding. The true nature of why these atoms bond to create molecules lies in quantum mechanics.
Molecular Bonding Through Quantum Mechanics
The key principle required to be able to understand why two atoms would choose to chemically bond is the idea that all natural systems (i.e. a collection of atoms) tend to adopt the state of lowest energy. As is the case with many other quantum mechanics problems, the easiest way to visualize molecular bonding is through the use of two hydrogen atoms.
The Hydrogen Atom
The hydrogen atom is comprised of a single proton and an electron that orbits the proton with said electron creating an electron cloud that surrounds the proton. This electron cloud represents the probabilistic area in which an electron is most likely to be found. As two single hydrogen atoms are introduced to each other, the attractive electrostatic potential force between the opposing electrons and protons increases and therefore starts to pull the two atoms closer together. This will continue until the repulsive electrostatic force between the two protons begins to push the two back apart until an equilibrium state is reached. Once this equilibrium state is reached, the electrons of the two atoms will become "shared" and the gap between the two protons will become part of a combined electron cloud as now the two electrons move freely between the two single protons. However, there is a question that arises from this: What about the repulsion electrostatic force between the two initially separate electron clouds? In this question, all forms of energy must be considered to fully grasp why the two electron clouds do not continue to repel the two atoms.
Types of Chemical Bonds
The three main types of bonding are ionic bonds, covalent bonds, and metallic bonds. Ionic bonds form between metals and nonmetals. Ionic bonding is caused by an attraction between oppositely charged ions. A common example of an ionic compound is table salt (NaCl). Covalent bonds are between nonmetals and involve sharing valence electrons to form molecules or large structures. A common example of a covalent molecule is water (H2O). Metallic bonds are between metals and are formed by metals sharing a "sea of electrons". A common example is the bonding between copper atoms. To explore the attractive and repulsive forces inside a dihydrogen molecule in this simulation.
Energy and the Hamiltonian
Reconsider the initial idea proposed that all natural systems prefer to be in the state of lowest energy. If such were to be the case, then all forms of energy must be considered for this system. The forms of energy found in this two hydrogen atom system are: the kinetic energy of each atom, the electric potential energy between the two protons, the electric potential energy between the two electrons, and the electric potential energy between each set of opposing electrons and protons. The sum of these four energies is what is called in quantum mechanics as the Hamiltonian. The Hamiltonian acts as the operator that corresponds to the energy of system when paired with the Schrodinger equation
[math]\displaystyle{ {\hat {H}} |\Psi \rangle =E|\Psi \rangle }[/math]
The equation for the Hamiltonian itself for the two hydrogen atom system is represented by
[math]\displaystyle{ H = \frac{-ℏ}{2m_{e}}(\nabla _{1}^{2} + \nabla _{2}^{2})+\frac{-ℏ}{2m_{p}}(\nabla _{A}^{2} + \nabla _{B}^{2}) - \frac{e^2}{4\Pi\varepsilon_{0}}(\frac{1}{r_{AB}}+\frac{1}{r_{12}}-\frac{1}{r_{1A}}-\frac{1}{r_{1B}}-\frac{1}{r_{2A}}-\frac{1}{r_{2B}}) }[/math]
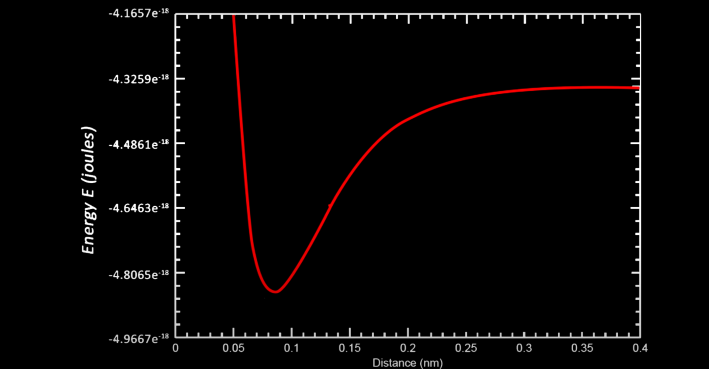
In this equation, 1A, 1B, 2A, and 2B denotations represent the relationship between an electron and proton while the AB denotation represents the relationship between the two protons, and the 12 denotation represents the relationship between the two electrons. Using this equation allows us to create this graph that shows the total energy of the system of the two hydrogen atoms as a function of the distance between the two
As it can be seen, when extremely close together, the total energy of the system is extremely high but as the two atoms gain separation, a small dip is created before the energy increases again and eventually levels off. This dip's lowest point corresponds to the equilibrium distance discussed earlier where the force of attraction between the electron and protons and the repulsion between protons and repulsion between electron clouds is equal as this is where energy is lowest and therefore this is where the atoms would idealistically be. From the graph as well it can be shown that if the data were to be extrapolated out for a distance between atoms to be approaching infinity, the value of energy would be greater than our lowest value of energy. This idea can be interepreted as to the reason why two separate atoms would chemically bond to each other as together their lowest energy would be lower than if the two were entirely separate (i.e. infinitely far apart).
Valence Shells and The Pauli Exclusion Principle
Another way of understanding this idea can be seen through the filling of valence shells for atoms. For example, atoms that are members of the halogen group are the most reactive or unstable atoms as they would like to fill their outer valence shell. This can be thought of as these atoms wanting to attain their lowest possible energy. If this is taken into account, it can be reasoned that unfilled valence shells will have more potential energy than filled valence shells. It can also be seen that the gaining of an extra electron to fill the valence shell will create more force of attraction than the force of repulsion as was demonstrated earlier by the two hydrogen atoms combining to make an [math]\displaystyle{ H_{2} }[/math] molecule. When this is taken into account, it can be seen that the lowest potential energies as functions of electrons are: 2 electrons, 10 electrons, 18 electrons, 36 electrons, 54 electrons, and 86 electrons. These numbers at first may seem random in their nature and one may ask why these specific numbers and for this, the Pauli Exclusion Principle helps to interpret. It goes to explain that two or more fermions, in our case electrons, cannot occupy the same quantum state within a single system. For this example, each energy shell of the atom will act as its own system. The larger question then becomes what constitutes a quantum state. A quantum state is composed of four variables that act as specific descriptors for the attributes of an electron. The four variables are
n: The energy level of the electron which can be given by the energy shell level the electron is in (i.e. energy shell 1, 2, 3, etc). These values must be whole positive integers.
l: The quantum angular momentum of the electron which can be given by n-1. These values must be whole positive integers or 0.
[math]\displaystyle{ m_{l} }[/math]: The magnetic quantum number of the electron which can be given by ±l. These values must be whole integers.
[math]\displaystyle{ m_{s} }[/math]: The spin of the electron which can only be either +[math]\displaystyle{ \frac{1}{2} }[/math] or -[math]\displaystyle{ \frac{1}{2} }[/math].
These four quantum numbers can then be arranged into unique sets that together describe the electron's quantum state. A table of these can be seen below
| n | l | [math]\displaystyle{ m_{l} }[/math] | [math]\displaystyle{ m_{s} }[/math] | combinations |
|---|---|---|---|---|
| 1 | 0 | 0 | ±[math]\displaystyle{ \frac{1}{2} }[/math] | 2 |
| 2 | 0, 1 | 0, ±1 | ±[math]\displaystyle{ \frac{1}{2} }[/math] | 10 |
| 3 | 0, 1, 2 | 0, ±1, ±2 | ±[math]\displaystyle{ \frac{1}{2} }[/math] | 18 |
| 4 | 0, 1, 2, 3 | 0, ±1, ±2, ±3 | ±[math]\displaystyle{ \frac{1}{2} }[/math] | 36 |
Uncoincidentally, the numbers for most stable electrons also align with the number combinations of quantum states for different energy shells. These correspond further as the 2 electrons represent the total electrons for a filled first energy shell, 10 electrons for a filled second energy shell, 18 electrons for a filled third energy shell, and so on. The table could be extrapolated further for all energy shell levels and the combinations would correctly correspond to the total number of electrons in an atom when that energy shell level is filled.
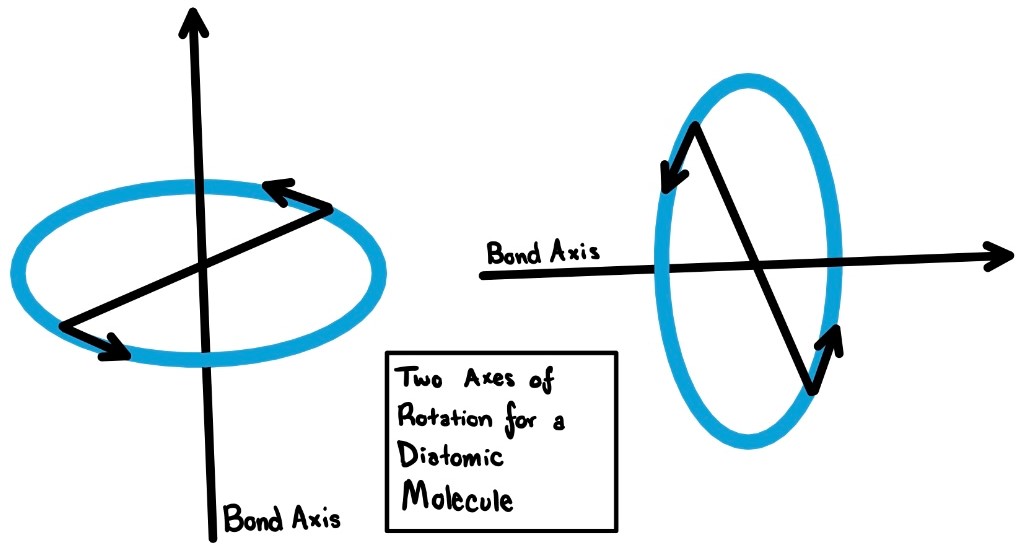
Angular Momentum in Diatomic Molecules
Quantum numbers l and [math]\displaystyle{ m_{l} }[/math] are determined by angular momentum. In molecules, the rotation of the molecule as a whole and the nuclei contribute to the total angular momentum. The two rotational axes are perpendicular (or orthogonal) to the bond axis. Therefore, diatomic molecules need to be described differently than atoms.
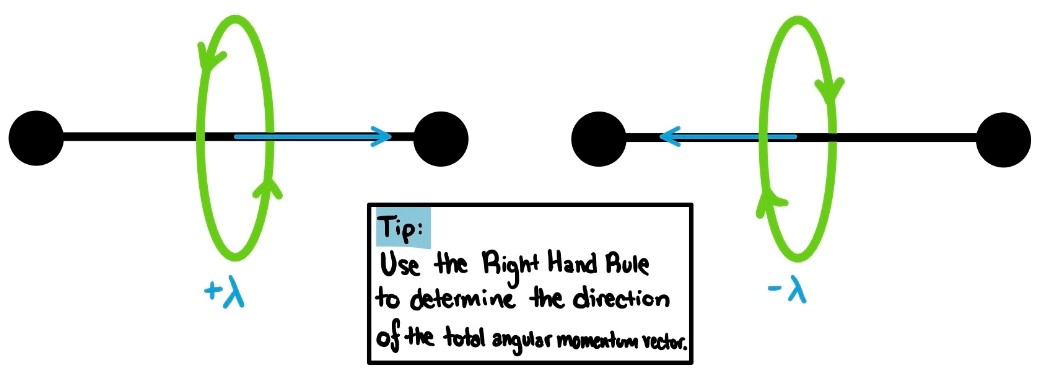
Like with atoms, quantum mechanics restricts values of the component of total angular momentum to integer multiples of ħ. For atoms, this quantum number is [math]\displaystyle{ m_{l} }[/math]. For molecules, this quantum number is denoted by 𝜆. Possible values for 𝜆 are: 𝜆 = 0, ±1, ±2, ±3, … In visualization, the angular momentum vector for rotation about the bond will lie along the bond axis. The sign of 𝜆 determines the direction of the total angular momentum vector.
Molecular orbitals are labeled based on the values of 𝜆. Below is a table that explains molecular orbitals determined by the absolute value of 𝜆 and equivalent atomic orbitals determined by l.
| 𝜆 | Molecular Orbital | l | Atomic Orbital |
|---|---|---|---|
| 0 | σ | 0 | s |
| 1 | 𝜋 | 1 | p |
| 2 | δ | 2 | d |
Quantum numbers for diatomic molecules doesn't stop here. The main attributes described by diatomic quantum numbers are rotation (total angular momentum), vibration, rovibrational spectra, and the principle quantum number.
Energy Levels
The energies involved with the motions of a molecule can be categorized into translation, rotational, and vibrational energies. Translational energy is equivalent to the Newtonian kinetic energy of the molecule. [math]\displaystyle{ E_{trans} = 1/2 mv^2 }[/math] where [math]\displaystyle{ m }[/math] is the mass of the molecule and [math]\displaystyle{ v }[/math] is the velocity of the molecule.
Rotational energy is the kinetic energy of rotation defined by [math]\displaystyle{ E_{rot} = L^2/2I }[/math] where [math]\displaystyle{ L }[/math] is the angular momentum and [math]\displaystyle{ I }[/math] is the moment of inertia of the molecule. For a microscopic system like a molecule, angular momentum is defined as [math]\displaystyle{ L^2 = l(l+1)ħ^2 }[/math] where [math]\displaystyle{ l }[/math] is a positive integer and [math]\displaystyle{ ħ }[/math] is the reduced Planck constant commonly referred to as “h-bar.” For a diatomic molecule, the moment of inertia is defined as [math]\displaystyle{ I = μr^2 }[/math] where [math]\displaystyle{ μ }[/math] is the reduced mass of a molecule and [math]\displaystyle{ r }[/math] is the average distance between the centers of two atoms in the molecule. Using the information from above and using substitution, the rotational energy levels of a diatomic molecule are given by: [math]\displaystyle{ E_{rot} = l(l+1)ħ^2/2μr^2 }[/math]
Vibrational energy is produced by each atom in a diatomic atom oscillating (or vibrating) along the line connecting them. The vibrational energy can be found using [math]\displaystyle{ E_{vib} = (n + 1/2)ħω }[/math] where [math]\displaystyle{ n }[/math] is a positive integer and [math]\displaystyle{ ω }[/math] is the angular frequency of vibration.
Computational Model
Molecules can be modeled in coding software like Glowscript. This link: https://trinket.io/embed/glowscript/6c8480b52c?start=result is a basic dihydrogen molecule. Follow the link and add more features! Try adding the total angular momentum vector to start.
Examples
These examples will be using a dihydrogen molecule. The mass of a hydrogen atom is 1.6735575 × 10^-27 kg. This dihydrogen molecule is in its ground state, has a velocity of 2000 m/s, and has an angular frequency of 13 Hz.
Simple
Question: What molecular orbit best described the dihydrogen molecule?
Solution: Each hydrogen in the dihydrogen molecule has one valence electron. Therefore, there are only two valence electrons. A hydrogen atom has quantum numbers [math]\displaystyle{ n }[/math] = 1, [math]\displaystyle{ l }[/math] = 0, [math]\displaystyle{ m_{l} }[/math], and [math]\displaystyle{ m_{s} }[/math] = [math]\displaystyle{ ±1/2 }[/math]. This corresponds to the 1s orbital. Comparing that to molecular orbits, 𝜆 must equal 0 so the molecular orbit is σ.
Middling
Question: What is the vibrational energy of the dihydrogen molecule?
Solution: For kinetic energy, substitute values into the kinetic energy equation. [math]\displaystyle{ E = 1/2 (1.6735575 × 10^{-27} kg)(2000 m/s)^2 = 6.69423 × 10^{-21} J }[/math]
Difficult
Question: What is the vibrational energy of the dihydrogen molecule?
Solution: Vibrational energy is equal to [math]\displaystyle{ E_{vib}=(n + 1/2)ħω }[/math]. Because the dihydrogen is at its ground state, let's say [math]\displaystyle{ n }[/math] (the vibration quantum number) is 0. Plugging in we have:
[math]\displaystyle{ E_{vib} = (0+1/2)(1.05457182 × 10^{-34} m^2 kg/s)(13 Hz) = 6.85471683 × 10^{-34} J }[/math]
Connectedness
Molecules are essential in building the world we live in today if it were not for them, the universe would be atom soup with no true forms of anything existing beyond single atom structures. Molecules allow for the vast diversity in forms of matter and are essential for the existence of anything outside of single atom structures. The understanding of how they are formed allows for a better understanding of how the world around us truly works and shows how often macroscopic ideas such as systems being in the lowest state of energy (i.e. a ball rolling down from the top of the hill) can be translated to the atomic level.
History
The term “molecule” originated from Rene Descartes, a French philosopher in the 1620s, from the French word “molécule” which means “extremely minute particle.” Although the term was used since the 1620s, the concept of molecules was accepted by many chemists as a result of Dalton’s Laws of Definite and Multiple Proportions (1803-1808) and Avogadro’s Law (1811). Some physicists, like Ludwig Boltzmann, James Clerk Maxwell, and Willard Gibbs, were resistant to the idea of the molecule and believed the concept was nothing more than a convenient mathematical construct. In 1911, Jean Perrin determined how to solve for Avogadro’s number (N) and confirmed the existence of molecules.
See also
Further reading
External links
Vibrational Energy levels (Diatomic molecule)