Magnetic Torque

Magnetic torque is induced when a magnetic field causes a current carrying coil of wire to twist.

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Example of Magnetic Torque

The Main Idea

The idea behind this concept is that as current flows through a wire, a magnetic field is produced. This magnetic field causes a force to act upon the wire causing it to twist. An example of this phenomenon is the movement of a compass needle by the Earth's magnetic field. Another example is a hanging coil that twists in the direction of the magnetic field of a bar magnet.

The magnetic torque acts on the dipole, and it is highly dependent on the magnetic moment and external magnetic field.

Several factors besides the magnetic moment and external magnetic field can affect the magnetic torque. In a loop or other three dimensional object the orientation of the object relative to the magnetic field highly affects the torque.

Through the following general example you can see how this phenomena occurs:

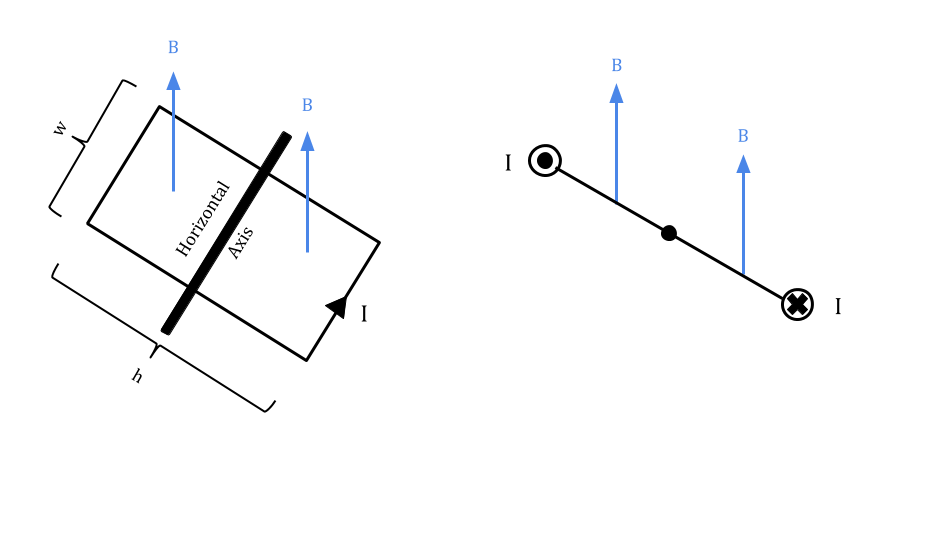
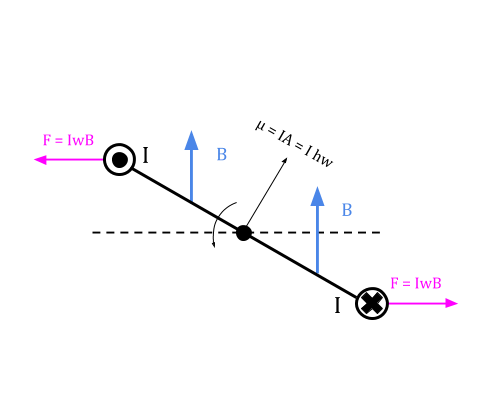
On the sides h, the magnetic force is horizontal pointing outwards causing the loop to stretch; while on the sides of length w the magnetic forces are horizontal and tend to make the loop twist on the axle. This causes the loop to rotate counterclockwise. When the plate of the loop is perpendicular to the magnetic field don't exert any twist.

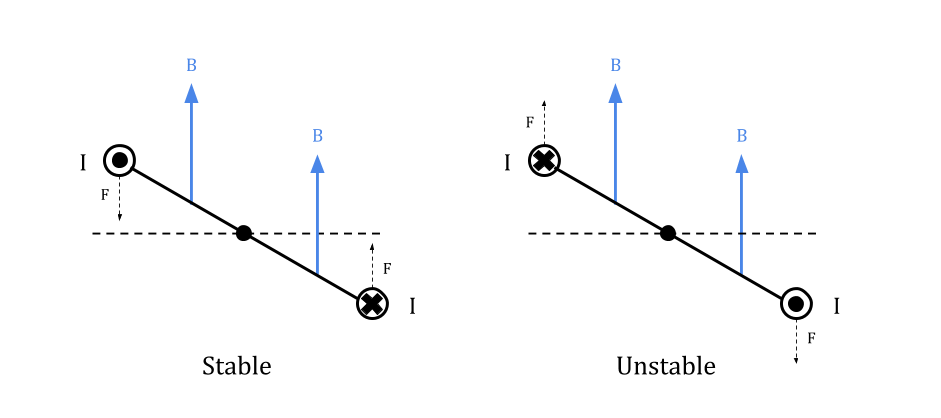
There are two configurations: Stable and Unstable

In the stable configuration, magnetic forces will twist the loop back up to the horizontal plane. In the unstable configuration, small displacement away from the horizontal leads to magnetic forces that rotate it even farther out of the plane.

This relationship can be seen in this video: [1]

Here is a video on Asymmetric Magnet Torque Asymmetric Magnet Torque

A Mathematical Model

The overarching equation that encapsulates this physical phenomena is as follows:

[math]\displaystyle{ \boldsymbol{\tau} = \boldsymbol{\mu} \times\mathbf{B} }[/math]

where:

τ is the variable describing torque

μ is the magnetic dipole and can be found using many expressions including that of a wire which relates magnetic dipole to the current in the wire multiplied by its cross sectional area. For a magnet, this quanity is not easily derived, and is a little outside the scope of this discussion. This quanitity is usually given in the problem statement. However, for a video that helps describe the magnetic dipole moment of a magnet: [2]

B is the magnetic field

The torque provided by each of the magnetic forces around the axle is equal to the distance from the axle times the component of the force perpendicular to the lever. Twist applied is due to the w - sides of the loop where torque acts out of the page. This causes a clockwise twist.

[math]\displaystyle{ F_{perpendicular} = I*w*B*sin(x) }[/math] where the arm is equal to h/2, each side exerts a force [math]\displaystyle{ F = 2(I*w*B*sin(x))(h/2) }[/math]

[math]\displaystyle{ τ = I*w*B*sin(x) }[/math] and [math]\displaystyle{ µ = I*w*h }[/math]

[math]\displaystyle{ τ = µ x B = µ*B*sin(x) }[/math]

The right hand rule for the direction of torque is as follows: the fingers of your right hand curl in the direction the loop will rotate, and your thumb will point the the direction of torque. The direction of the torque vector will be along the axle around which the loop rotates. For a more in depth explanation of the right hand rule see Right-Hand Rule

Magnetic Dipole Moment

The magnetic dipole moment of a current carrying loop of wire, µ, is defined as a vector pointing in the direction of the magnetic dipole (South to North) perpendicular to the plane created by the wire loop, and its direction is determined by using the right hand rule (fingers curling along the direction of the current, thumb pointing in dipole direction.)

[math]\displaystyle{ µ = I*A = I*w*h }[/math]

The coil tends to twist in a direction to make µ line up with B.

Units Discussion

τ has units of N*m

µ has units of A*m^2

B has units of tesla or T

From this, it must be that one N*m (which interestingly defines work) is equal to one tesla * A*m^2. From a discussion of units alone, it is important to think about what sorts of questions the professor might ask, meaning questions could include an analyses of the work that must be added to a system to keep it stationary for example.

A Computational Model

Click here to view the PHET Interactive Model created by the University of Colorado

PHET Interactive Magnet and Compass Model

Examples

Essentially, there are only a few categories of questions that can be asked relating to magnetic torque. These questions include a simple computation of magnetic torque given the dipole moment of a magnet, and the magnetic field being applied to the observation location. In this situation, you can either utilize a simple cross product, as in the equation listed above, or if the values are given as scalars, and it is known that they are perpendicular to each other in direction, you can utilize the equation: [math]\displaystyle{ |τ| = |µ| * |B|cos(90) = |µ| * |B| }[/math]. This is the essential question involving the equation listed above for magnetic torque. However, the professor can also ask questions relating to material learned from physics 1 involving angular frequencies and other products of angular momentum.

Torque on Current Carrying Loop

Simple

A bar magnet whose magnetic dipole moment is <3, 0, 1.8> A · m2 is suspended from a thread in a region where external coils apply a magnetic field of <0.6, 0, 0> T. What is the vector torque that acts on the bar magnet?

Middling

A bar magnet whose magnetic dipole moment is 14 A · m2 is aligned with an applied magnetic field of 5.4 T. How much work must you do to rotate the bar magnet 180° to point in the direction opposite to the magnetic field?

Difficult

A cylindrical bar magnet whose mass is 0.09 kg, diameter is 1 cm, length is 3 cm, and whose magnetic dipole moment is <4, 0, 0> A · m2 is suspended on a low-friction pivot in a region where external coils apply a magnetic field of <2.0, 0, 0> T. You rotate the bar magnet slightly in the horizontal plane and release it. (For small angles in radians, assume sin(θ) ≈ θ.)

(a) What is the angular frequency of the oscillating magnet?

(b) What would be the angular frequency if the applied magnetic field were <4.0, 0, 0> T?

A detailed description and symbolic representation of magnetic torque can be seen here: Magnetic Torque and Magnetic Dipole Moment

Connectedness

A standard compass http://helenotway.edublogs.org/2011/01/02/different-compass-point-same-ultimate-direction/

Utilizing a compass is a basic survival need and it just so happens to depend on the torque produced by the Earth's magnetic field. As a Biology major, field work is a large part of what I do, especially studying ecological systems and different habitats. In order to navigate in unfamiliar locations, such as deserts and dense tropical forests, scientists rely heavily on basic survival skills and this includes the use of compasses and maps. Physics, biology, and chemistry make up part of the science family and each heavily depends on the other, this is why it is important to study each one to bridge the relationship.

First paragraph of "Connectedness" written by Demetria Hubbard 2015

The Earth has a complex magnetic field and magnetic dipole moment that creates a magnetic torque. The necessity of all three of these magnetic properties is rarely known; however, all three are essential for life on earth. Earth's magnetic field serves to deflect most of the solar wind, so without the magnetic properties of the earth, the charged solar wind would have stripped the ozone layer from earth which would have exposed everything on earth to dangerous UV radiation.

One interesting development in the field of magnetic torque is the experimentation, and initial prototyping of magnetic gears for application in a wide variety of industries, but that has a main focus in the wind turbine industry. The issue with strictly mechanical gearing today is in a high stress situation, the “teeth” or connection between gears, will fracture as a result of being over torqued. This results in a very powerful stall out that can gravely damage the broader mechanics of the instrument that the gears are in. Magnetic gears provide an interesting solution to the problem because there is no “physical” interaction between gear faces, only magnetic forces. This mitigates the stalling issue and provides a higher torque range by which machines utilizing this technology can operate. Just to give a specific example of this application, in the oil drilling industry, specifically where mud motors are applied to prospect oil, there is an incredible amount of power that must be applied via torque translation from the power section to the drill bit. An issue often seen is the wearing down of gears along the drill chain as a result of lubrication leaking, and rubbing of two components together, leading to stall outs which can damage the drill overall. To counteract this problem, research has been started to develop magnetic transmission sections to transmit the torque provided by the power section to the drill bit with minimal part damage due to minimal rubbing of components. The introduction of the magnetic gear will also mitigate the cost of lubricants, which is a very high cost especially when expensive lubricants are required.

History

Refer to Magnetic Force

The great importance of magnetic torque that is used in compasses cannot be ignored. The history of the compass and earth's magnetic field are very valuable. The tendency of a magnet to align itself was discovered by the Chinese about 2000 years ago. The magnetic compass became a valuable commodity to European navigators in the 12th century, and in 1600, William Gilbert published De Magnete, which concluded that the earth behaves as a giant magnet. Several theories since then have been made to explain how a magnetic field is produced by the earth. The most accepted theory is that the energy from the radioactivity of the earth's core travels outwards as heat. This heat produces a thermal convection core that creates the earth's magnetic field.

Magnetic Torque

Contents

The Main Idea

A Mathematical Model

Magnetic Dipole Moment

Units Discussion

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu